基于ODR-ADASYN-SVM的极端金融风险预警研究①

林　宇， 黄　迅， 淳伟德， 黄登仕

(1. 成都理工大学商学院， 成都 610059； 2. 西南交通大学经济管理学院， 成都 610031)

基于ODR-ADASYN-SVM的极端金融风险预警研究①

林宇1， 黄迅1， 淳伟德1， 黄登仕2

(1. 成都理工大学商学院， 成都 610059； 2. 西南交通大学经济管理学院， 成都 610031)

摘要:针对合成少数类过采样(synthetic minority over-sampling technique, SMOTE)方法在提升支持向量机(support vector machine, SVM)的非均衡样本学习能力中出现的过拟合(over fitting)，引入自适应合成抽样方法(adaptive synthetic sampling approach, ADASYN)和逐级优化递减欠采样方法(optimization of decreasing reduction, ODR)分别克服SMOTE在生成新样本中的盲目性和在处理对象上的局限性，进而与SVM相结合，构造出改进SVM，即ODR-ADASYN-SVM模型来预测中国极端金融风险；最后运用T检验对各模型预测精度的差异性进行显著性检验以及对各模型的预测稳定性进行评价.实证结果表明， ODR-ADASYN-SVM模型不仅能够显著地提升SVM的非均衡样本学习能力，同时也能够有效地克服SMOTE的过拟合，从而展示出优越的极端金融风险预测性能.

关键词:ODR； ADASYN； 支持向量机； 极端金融风险； 预警模型

0引言

近年来爆发的次贷危机、欧债危机等金融风险危机事件，不仅给各国经济带来了沉重打击，也使金融风险预警面临着更为严峻的挑战.因此，建立科学的风险预警模型，准确地识别并有效地防范和控制风险，以维护金融经济安全，促进经济社会和谐稳定，既是新形势下金融经济管理部门面临的重要任务，也是学术界关注的热点问题.

然而，无论是对金融经济管理部门还是对投资者来说，都更关注金融市场极端下滑(extreme downside)所引发的极端金融风险(extremely financial risk)[1].这是因为，极端金融风险尽管发生概率极小，但一旦发生，就不仅会给投资者带来巨大损失，或是灭顶之灾，甚至还可能引起社会动荡、政权解体等严重后果.因此，探讨极端金融风险的有效预警方法具有至关重要的现实意义.

在这里需要指出的是，自从1997年东南亚金融危机发生以来，极端金融风险预警就一直都是学术界关注的焦点与热点.学者们已运用概率比(probit)回归、横截面回归(STV)、信号法(KLR模型)、逻辑(Logit)回归、神经网络(neural network, NN)等模型对金融风险危机预警展开了研究[2-6]，虽然在预测极端金融风险上都取得了较好的效果，但却存在前提条件过于苛刻、过学习、欠学习以及局部极小等问题[7].而SVM[8]运用计算机智能技术自动确定模型结构，不仅能有效克服上述模型所存在的问题，而且也具有优越的智能学习与智能预测能力，因而被广泛运用于风险预警中且取得了良好的研究效果[9].然而，SVM的良好预测性能却需要依赖数量相同的不同类别样本进行学习才能获得，事实上，现实生活中大量存在的样本却往往属于非均衡的[10]，如金融市场中的极端与非极端金融危机事件所分别代表的少数和多数类样本就正好构成一类典型的非均衡样本.如果仍然运用SVM对这样一类非均衡样本进行学习，就很可能会造成SVM的分类超平面(separating hyperplane)向极端金融危机事件所代表的少数类样本偏移，从而导致该类样本被大量错分，最终降低SVM的预测性能[11].由此可见，非均衡样本使得SVM学习面临严峻的挑战，因而就必须改进SVM模型，以提升SVM的非均衡样本学习能力.

尽管学者们已研究出多种方法，尤其是研究出SMOTE方法[12]来提升分类模型的非均衡样本学习能力.但在SMOTE方法中，每个少数类样本都盲目地生成相同数量的人造样本，却忽略了其邻近样本的分布特点，因而容易造成少数类样本的相互重叠.同时，SMOTE也仅仅处理少数类样本，无法实现对多数类样本的处理.因此，SMOTE方法在生成少数类样本中的盲目性以及在处理对象上的局限性，使得分类模型不仅容易错分少数类样本，而且也无法有效删除多数类样本中的噪声信息，从而出现不能准确预测少数类样本的过拟合问题[13].而ADASYN[14]却是专门针对SMOTE的盲目性而设计的解决方法，它利用少数类样本的密度分布来计算少数类样本生成的数量，使学习困难的少数类样本生成更多的人造样本，以增强分类模型的学习能力.同时，ODR[15]利用K最邻近规则(K-nearest neighbor，KNN)来计算多数类样本对邻近样本的影响程度，进而依次删除对分类模型的学习能力有负面影响或者影响不大的多数类样本，以实现对多数类样本有目的的筛选，从而有效克服SMOTE在处理对象上存在的局限性.由此可见，将ADASYN和ODR相结合，既能有效地克服SMOTE在生成少数类样本中的盲目性，又能有效地克服SMOTE在处理对象上的局限性，因而在提升非均衡样本学习能力上具有十分显著的优势.但令人遗憾的是，就本文所掌握的文献而言，尚未发现有学者将ADASYN与ODR相结合以提升分类模型的非均衡样本学习能力.

值得注意的是，中国金融市场成立时间较短，缺乏应对金融风险危机的成熟经验，在极端金融风险的控制与防范上还存在诸多薄弱性[16-17]；与此同时，随着经济全球化的深入发展，中国金融市场与国外金融市场的联系日益密切，因而极易受到国外极端金融风险的传染与冲击，从而承受着更为艰巨的风险考验，面临着更为严峻的风险挑战[18-19].那么，能否将ODR、ADASYN与SVM相结合，构建出适合中国金融市场的极端金融风险预警方法？如果能，那么在极端金融风险的预测上，构建的预警模型又是否较SVM、SMOTE-SVM、ODR-SVM以及ADASYN-SVM预警模型具有更为明显的优势呢？

基于以上分析，本文以沪深300指数(China securities index 300, CSI300)为研究对象，既引入ADASYN来克服SMOTE在生成新样本中的盲目性.又针对SMOTE在处理对象上的局限性，引入ODR来删除非极端金融风险样本中的噪声信息；并与SVM相结合，提出改进SVM，即ODR-ADASYN-SVM预警模型来预测中国极端金融风险.进而运用性能评估指标对SVM、SMOTE-SVM、ODR-SVM、ADASYN-SVM以及ODR-ADASYN-SVM模型的预测精度进行评估，并运用T检验对各模型预测精度的差异性进行显著性检验并对各模型的预测稳定性进行评价，以充分展示出ODR-ADASYN-SVM模型在预测性能上的显著优越性，从而为金融经济管理部门及时控制与防范极端金融风险以及投资者制定合理的投资策略提供良好的决策借鉴.

目前，国内外已有部分学者运用SVM对金融市场风险预警展开了研究.Ahn等[20]以韩国金融市场为研究对象，建立了SVM金融市场风险预警系统；Groth和Muntermann[21]又以文本信息为研究对象，运用支持向量机(SVM)、神经网络(NN)、贝叶斯(Bayes)等方法，探索了金融市场风险危机管理；徐国祥和杨振建[22]将主成分分析方法(principle component analysis, PCA)、遗传算法(genetic algorithm, GA)和SVM相结合，构建了PCA-GA-SVM预警模型，并对沪深300指数和大盘股走势进行了预测研究；李云飞和惠晓峰[23]运用SVM建立了股票投资价值分类模型，并与BP和RBF神经网络的预测性能进行了比较.

与本文所掌握的研究文献相比，本文的差异性显而易见.1)尚未发现有文献集成ODR和ADASYN来克服SMOTE所存在的过拟合，尤其是没有发现有文献将SVM与该技术相结合，对中国新兴金融市场(本文用CSI300作为中国新兴金融市场的代表)的极端金融风险展开预警研究；2)除运用常用指标来评价非均衡样本分类模型的性能之外，本文尤其是运用T检验对模型预测精度的差异性进行显著性检验，以及对各模型的预测稳定性进行评价；3)在提取能够显著刻画中国新兴金融市场极端金融风险的特征指标上，不仅运用统计假设检验和逐步判别分析法来提取市场内部特征指标，还运用Copula方法专门对市场外部特征指标进行了提取，从而使得提取出的特征指标能够更为全面而显著地刻画中国新兴金融市场的极端金融风险.

1研究方法

1.1极端金融风险SVM预警方法

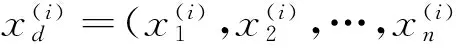
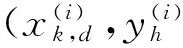
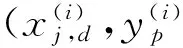
y(i)=sgn(f(x))

(1)

式中sgn(f(x))是符号函数；f(x)是以特征指标变量为自变量的决策函数.当金融市场处于极端金融风险状态时，y(i)=sgn(f(x))=+1；否则，就为-1.

运用SVM方法在训练集上寻找最优分类函数(即式(1)代表的极端金融风险预警模型)，就需要将寻找最优分类函数转化为求解以下最优问题

(2)

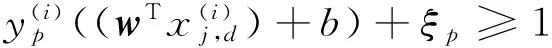
(3)

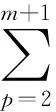
为了求解上述最优问题，就要利用拉格朗日乘子(Lagrangemultiplier)法将上述最优问题转化为对偶(dual)问题

(4)

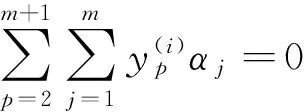
(5)

0≤αj≤C,j=1,2,…,m

(6)

于是，通过求解上述对偶问题，就得到以下最优分类函数f(x)=sgn(w*x+b*)

(7)

其中

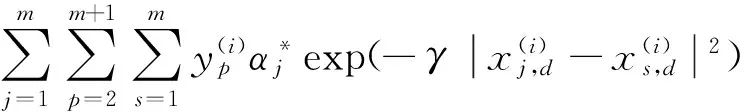
(8)

至此，极端金融风险预警的SVM方法就已构建完毕.然而，正如前文所分析的那样，由极端与非极端金融风险样本所构成的非均衡训练样本会大大削弱SVM的学习能力，最终降低SVM对极端金融风险样本预测的精度.因此，下文将重点探讨能够提升SVM的非均衡样本学习能力的有效方法，以降低数据的过度偏斜对SVM预测极端金融风险样本所造成的影响.1.2提升SVM预测性能的ODR-ADASYN方法

为克服SMOTE在生成新样本中的盲目性以及在处理对象上的局限性，本文运用ODR和ADASYN方法来改进SMOTE，以提升SVM的极端金融风险预测性能.

假定训练样本集为S，其中非极端金融风险样本集为Smaj，极端金融风险样本集为Smin，x属于Smaj中的样本.定义样本x的关联集是指Smaj中除x以外的其他非极端金融风险样本的K个最邻近样本中包含x的样本集，简称为关联集x.则ODR-ADASYN的计算机实验步骤如下：

步骤1根据式(9)，计算出需要删除的非极端金融风险样本数量Num

(9)

其中α∈[0,1]，表示删除指定的非极端金融风险样本后期望得到的样本非均衡水平，若α=1，则表示删除指定的非极端金融风险样本后，两类样本数量达到完全均衡；

步骤2计算出非极端金融风险样本集中每个样本的关联集；

步骤3就样本x而言，运用KNN算法对关联集x中的所有样本进行分类，能够被正确分类的个数记录为withx；

步骤4从关联集x包含的所有样本的最邻近样本中将样本x删除，并将第K+1个最邻近样本加入，再运用KNN算法对关联集x中的所有样本进行分类，能够被正确分类的个数记录为withoutx；

步骤5根据式(10)，计算withx与withoutx的差值diffdiff=withx-withoutx

(10)

并通过下式判断diff与0的大小关系来定义样本x的属性

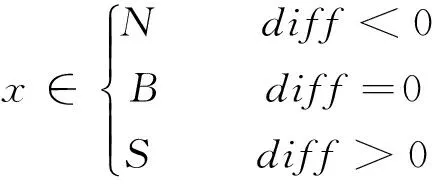
(11)

其中N代表噪声样本，B代表边界样本，S代表安全样本；

步骤6根据步骤3至步骤5，定义出Smaj中除样本x外的其余每个非极端金融风险样本的属性；

步骤7根据步骤6定义出的样本属性，保留Smaj中的边界样本且删除噪声样本，并针对安全样本作下一步处理；

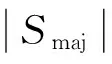
(12)

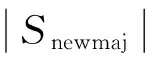
(13)

从式(13)可知，当合成数量为Numnew的人造极端金融风险样本后，两类样本数量就达到了完全均衡；

步骤10对每一个极端金融风险样本xi而言，从所有样本中找出其K个最邻近样本，并根据下式计算出最邻近样本中非极端金融风险样本的占比ri

(14)

其中Δi∈[0,1]，指K个最邻近样本中属于非极端金融风险样本的个数；

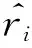
(15)

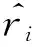
(16)

步骤12计算出每一个极端金融风险样本需要合成的人造样本个数gi

(17)

步骤13对每一个极端金融风险样本xi而言，都运用SMOTE方法合成gi个极端金融风险样本，此时两类样本数量达到一致.

需要说明的是，步骤1至步骤8是ODR的实验步骤，步骤9至步骤13是ADASYN的实验步骤.于是，就能够基于上述ODR-ADASYN的实验步骤平衡非均衡的训练样本，进而运用SVM对得到的均衡训练样本进行训练，最后再基于测试样本对通过训练得到的SVM模型进行性能测试与评价.

1.3极端金融风险预警模型的性能评估指标

基于均衡样本构建预警模型时，通常以分类准确率为评估指标来评价模型性能.然而，当样本非均衡时，该指标仅能刻画模型的整体预测性能，却无法有效地评估模型对于极端金融风险样本的预测性能[27].基于此，本文运用目前针对非均衡样本分类的常用评估指标——几何平均正确率Gmean、少数类的Fmeasure和AUC(area under ROC curve)值，对本文所提出的极端金融风险预警模型进行性能评估(以下用G和F分别代替Gmean和Fmeasure).3种评估指标的构建过程如下：

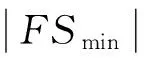
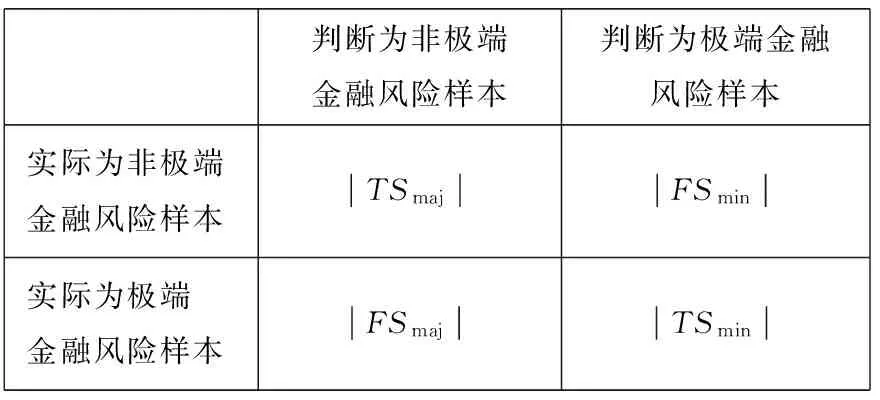
表1　二分类数据集的混淆矩阵

根据混淆矩阵并通过下面3个式子就可以得到灵敏度SE、特异度SP和极端金融风险样本查准率P3类基本指标

(18)

(19)

(20)

于是，再根据上述3类基本指标并通过下面两式就得到几何平均正确率G以及少数类的F

(21)

(22)

其中几何平均正确率G综合考察了模型对于两类样本的预测性能，若G较大，则说明模型预测两类样本的精度都较高，反之亦然；而少数类样本的F主要考察了模型对极端金融风险样本的预测性能，若F较大，就说明模型预测极端金融风险样本的性能较优越，反之亦然.此外，AUC代表受试者工作特征曲线(receiver operating characteristic, ROC)下方的面积.面积越大，说明模型对两类样本的综合预测性能越优异.

2实证结果与分析

2.1样本选择

本文选取沪深300指数(CSI300)2005-04-08～2012-12-31的样本作为研究对象.需要说明的是，之所以选择CSI300进行研究，原因在于CSI300包含了沪深股市60%左右的市值，被视为反映沪深两市整体走势的“晴雨表”，具有良好的市场代表性[22,28-29]，而之所以选择从CSI300创建以来至2012年末这段时间为研究区间，是因为沪深股市在这段时间内经历了暴涨暴跌的全过程，从而使沪深股市整体走势的预测结果具有更强的说服力.

2.2状态指标变量的确定

要确定出所选每个样本的状态指标变量，即确定出所选的每个样本究竟属于极端金融风险样本还是非极端金融风险样本，关键在于选择极端金融风险门槛值.只有选择出门槛值，才能以该门槛值为标准，将超过门槛值的样本认定为极端金融风险样本，未超过门槛值的样本认定为非极端金融风险样本，以确定出所有样本的状态指标变量，从而才能进一步开展预警模型的构建工作.

需要指出的是，目前还没有确定门槛值的最优数学理论模型.Hill[30]尝试运用Hill图法来确定门槛值；Stelios和Dimitris[31]则运用了超额均值函数(mean excess function, MEF)图法来确定门槛值；而Neftci[32]把1.65σ当作门槛值，超过1.65σ的值被作为极端金融风险样本；另外，DuMouchel[33]选择了10%左右的数据作为极端金融风险样本进行研究，取得了较好的研究效果.因此，本文选取占总体样本9%的收益率最低的样本作为极端金融风险样本，即极值尾部.由于根据极值理论(extreme value theory, EVT)，对于充分高的门槛值，超过门槛值的样本都近似服从广义帕累托分布(generalized Pareto distribution, GPD)簇，用下式表示

(23)

其中k表示超过门槛值的极端金融风险样本的个数；Fk(x)为极值分布函数；Gξ,β(x)为GPD簇分布函数.因此，本文还对这些极值尾部样本用准极大似然估计方法(quasi maximum likelihood estimation, QMLE)估计GPD簇分布函数的参数得到尾部GPD分布曲线与经验分布的拟合效果图(见图1).从图1可以直观地看出，GPD与经验分布具有较好的拟合效果，说明设定的极端金融风险样本门槛值是科学合理的.此时，极端与非极端金融风险样本的非均衡比例达到1∶10.

图1　CSI 300标准收益尾部经验分布与GPD分布拟合效果图

2.3特征指标变量的选择与提取

金融风险管理的目标在于建立有效的风险预警系统.而风险预警的重点又在于准确地提取出诱发金融市场爆发极端风险的特征指标.但极端风险的爆发，不仅是市场自身风险的累积，也有外部极端风险危机的传导作用.因此，本文通过借鉴相关文献[22,34]选择出由8项股指基本指标构成的内部特征指标.同时，由于相关文献[35-36]将具有代表性的国际金融市场作为了中国金融市场的外部风险危机因素，又考虑到收益率是反映市场综合信息的重要指标，因此，本文将8个具有代表性的国际金融市场的股指日收益率作为了外部特征指标(见表2).

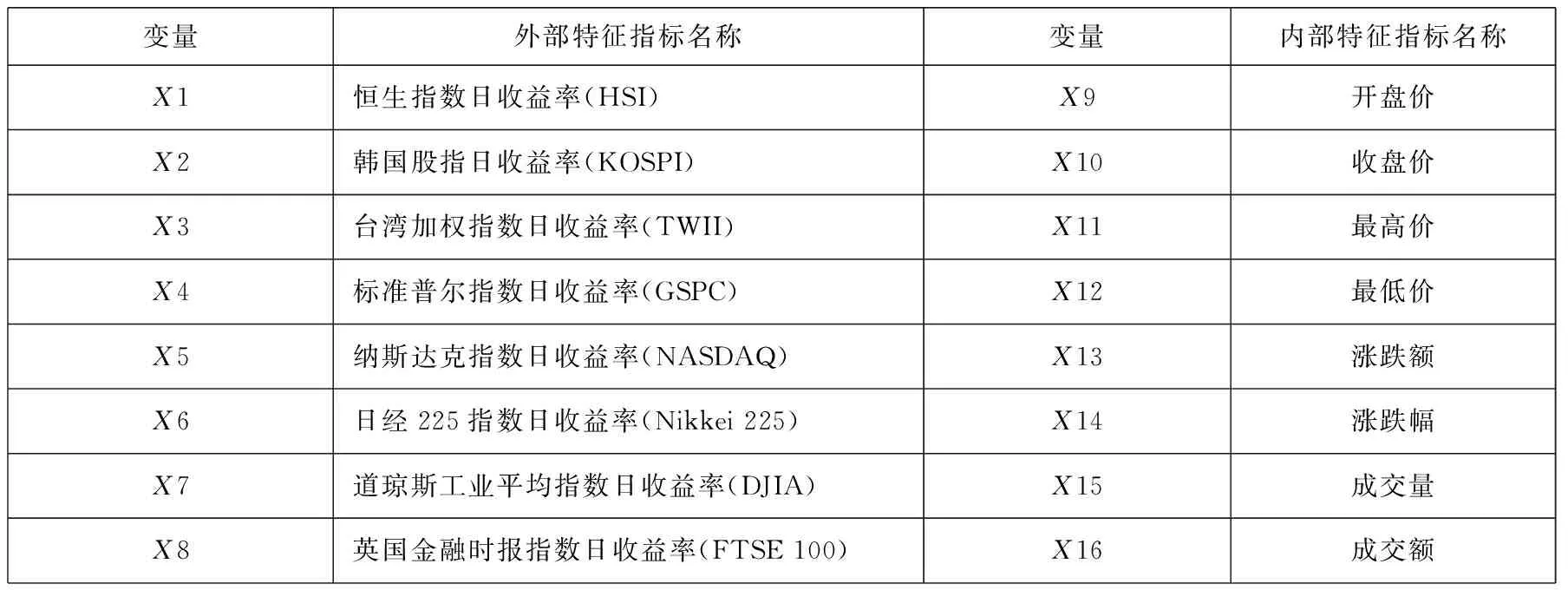
表2　极端金融风险预警模型的特征指标

注:样本的特征指标数据来源于雅虎财经(http://finance.yahoo.com)．

然而，最终用于预警的指标不仅是可以量化的，而且还需要存在显著差异，这样才可以起到预警效果.同时，宋新平和丁永生[26]也指出，预警是个多指标的复杂系统，提取合适的特征指标可以有效地提升模型的性能.因此，为了从上述指标中进一步提取出能够显著刻画中国新兴金融市场极端风险的市场内外部特征指标，本文还将对表2中的国外股市指标和基本指标分别作如下处理.

一方面，为了提取出对中国极端风险的爆发具有显著传导作用的外部特征指标，本文运用Clayton Copula对CSI 300日收益率和表2中的前8项国外股指日收益率的下尾相关性进行分析.这是因为下尾相关性能够反映两个市场同时暴跌的概率，这正好能够刻画外部极端金融风险对中国极端金融风险的影响程度[37].而Clayton Copula又恰好是专门刻画下尾相关性的Copula模型.由此，计算出CSI 300与各国外股指间的下尾相依系数(见表3).

表3　CSI 300与其余收益率之间的下尾相依系

从表3可以看出，CSI 300与HSI、KOSPI和TWII的下尾相依系数大于0.1，与Nikkei 225和FTSE 100的下尾相依系数小于0.1，而与美国股市3大指数(GSPC，NASDAQ和DJIA)的下尾相依系数几乎为0.从而说明，CSI300与HSI、KOSPI和TWII的下尾相关性较高，与Nikkei 225和FTSE 100的下尾相关性较低，而与美国股市3大指数(GSPC，NASDAQ和DJIA)几乎不存在下尾相关性.基于此，本文选择与CSI 300下尾相关性较高的HSI、KOSPI和TWII的日收益率作为最终的外部特征指标.

另外，为了检验上述提出的Clayton Copula模型是否充分描述了CSI 300与国外股指之间的下尾相依关系，本文还将进行卡方检验，结果见表4.从表4可见，在5%的显著性水平下，各卡方检验值都通过了拟合优度检验，由此证明CSI 300与国外股指存在的相依结构科学合理.另外，由于CSI300与HSI、KOSPI和TWII在2005-04-08～2012-12-31这段区间内的样本不匹配而出现缺失数据，因此，针对这些缺失数据，本文的处理方式是假如某个市场因节假日而没有进行交易，则其余市场的当日样本数据就被删除.最终选择出1 767个样本进行研究.

另一方面，为提取出能够显著区分风险状态的内部特征指标，本文还借鉴相关文献[26, 38]提出的统计假设检验方法和逐步判别分析法对表1中后8项基本指标进行提取.首先对这8项基本指标进行正态性检验，进而对符合与不符合正态分布的基本指标分别做单样本T检验和K-S检验，从中提取出若干基本指标；然后，运用逐步判别分析法进一步提取基本指标；最终将这8项基本指标约简为开盘价、收盘价、成交量和成交额这4项基本指标.并与通过Clayton Copula提取出的HSI、KOSPI和TWII日收益率这3项国外股市指标共同构成最终的能够显著刻画中国新兴金融市场极端金融风险的市场内外部特征指标.

表4　卡方检验统计量

2.4最优ODR-ADASYN-SVM预警模型的确立

在将SVM的核函数设为RBF核函数、惩罚参数C设为0.5、核函数参数γ设为0.5的基础上，本文采用10折交叉验证法(cross validation, CV)对ODR与ADASYN的最邻近参数K以及ODR中的参数α进行讨论，从而选择出性能最优的ODR-ADASYN-SVM模型.需要强调的是，之所以将惩罚参数C值与核函数参数γ值都设为0.5，是因为本文经过反复实验，最后确定模型在这两个值上的预测效果最为理想.本文主要使用Matlab 2011b进行编程分析.实验结果如图2和图3所示.

图2不同最邻近参数K下，参数α对模型预测精度的影响

Fig.2 Influence of parameter alpha on prediction accuracy in different nearest neighborK

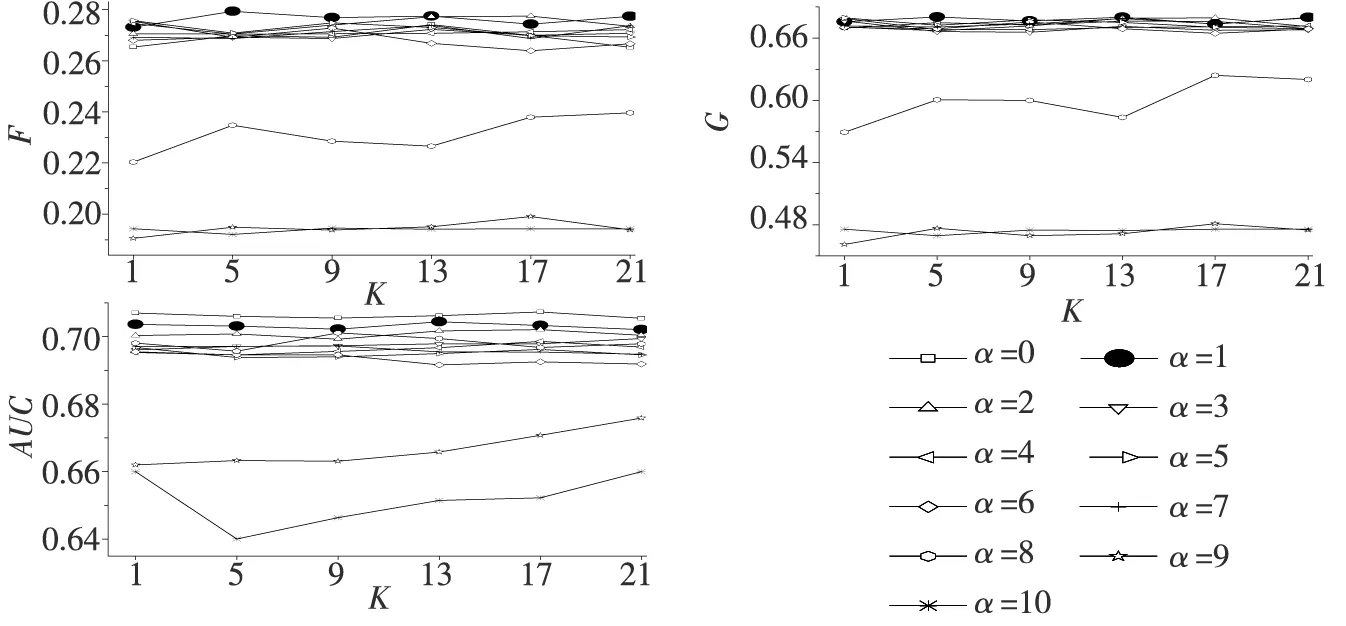
图3　不同参数α下，最邻近参数K对模型预测精度的影响

从图2可以看出，不论K取何值，随着参数α的增大，特别是当α>0.7时，模型的F和G值都同时呈现出明显的下降趋势，但当α≤0.7时，模型的F和G值却无明显的波动.此外，当α>0.8时，模型的AUC值同样也下降明显，但当α≤0.8时，模型的AUC值却无明显波动.由此说明，尽管ODR能够有效地删除非极端金融风险样本的噪声信息，但过大的α会使得ODR过多地删除有效的非极端金融风险样本，最终降低模型的预测精度.

而从图3可以看出，在绝大部分的α值下，随着K的增大，模型的G、F和AUC值都无明显波动，从而说明K对模型的预测精度影响不大.分析原因，主要在于当样本的非均衡水平较高时，极端金融风险样本的数量十分稀少，这使得每个样本的K个最邻近样本中属于极端金融风险类的样本较少且数量较为固定，并不会随着K的增大而增加，从而使得模型的预测精度较为稳定.

基于上述分析，本文认为，选择合适的α，对于构建精度最优的ODR-ADASYN-SVM预警模型起着至关重要的作用.因而，再次分析图2和图3可知，较其余绝大部分α下的ODR-ADASYN-SVM，α为0.1下的ODR-ADASYN-SVM具有最高的预测精度，特别是α为0.1、K为5下ODR-ADASYN-SVM模型的AUC值达到0.703 1，G值达到0.680 4，F值达到0.279 3，相比其他α与K值下的ODR-ADASYN-SVM模型，其预测精度最为优异.

2.5最优ODR-ADASYN-SVM模型与其余模型的预测性能对比评估

尽管通过上述实验，本文选择出最优的ODR-ADASYN-SVM预警模型，然而，该模型是否有效地提升了SVM的非均衡样本学习能力并成功地克服了SMOTE的过拟合，这是本文接下来需要继续深入探讨的内容.

在将SVM的核函数设为RBF核函数、惩罚参数C设为0.5、核函数参数γ设为0.5、最邻近参数K设为5、ODR-ADASYN-SVM中ODR的参数α设为0.1、ODR-SVM中ODR的参数α设为1的基础上，本文仍然采用10折交叉验证法对SVM、SMOTE-SVM、ODR-SVM、ADASYN-SVM和ODR-ADASYN-SVM模型的预测性能进行对比研究.实验结果如表5所示.

表5　模型预测精度的对比结果

注:产生NAN的原因在于SVM将CSI300的所有极端金融

从表5可以看出，SVM模型的预测性能最不理想，尤其是它的G值为0而F值为NAN的实证结果充分说明SVM模型将所有的极端金融风险样本都错误地判定为非极端金融风险样本，由此证明SVM模型无法有效地预测极端金融风险.从表5还可以看出，ODR-ADASYN-SVM模型在G、F值上都高于SMOTE-SVM、ODR-SVM和ADASYN-SVM模型，而在AUC值上略低于SMOTE-SVM和ADASYN-SVM模型，该结果能够说明，从预测精度的角度，ODR-ADASYN-SVM模型的预测性能明显优于ODR-SVM模型且略优于SMOTE-SVM和ADASYN-SVM模型.

然而，仅根据各评估指标值就判断模型的性能还缺少类似于统计学检验所具有的科学性与客观性.因此，本文还将对预测结果进行配对样本T检验，从而检验出各模型的预测性能差异是否显著.检验结果如表6所示.

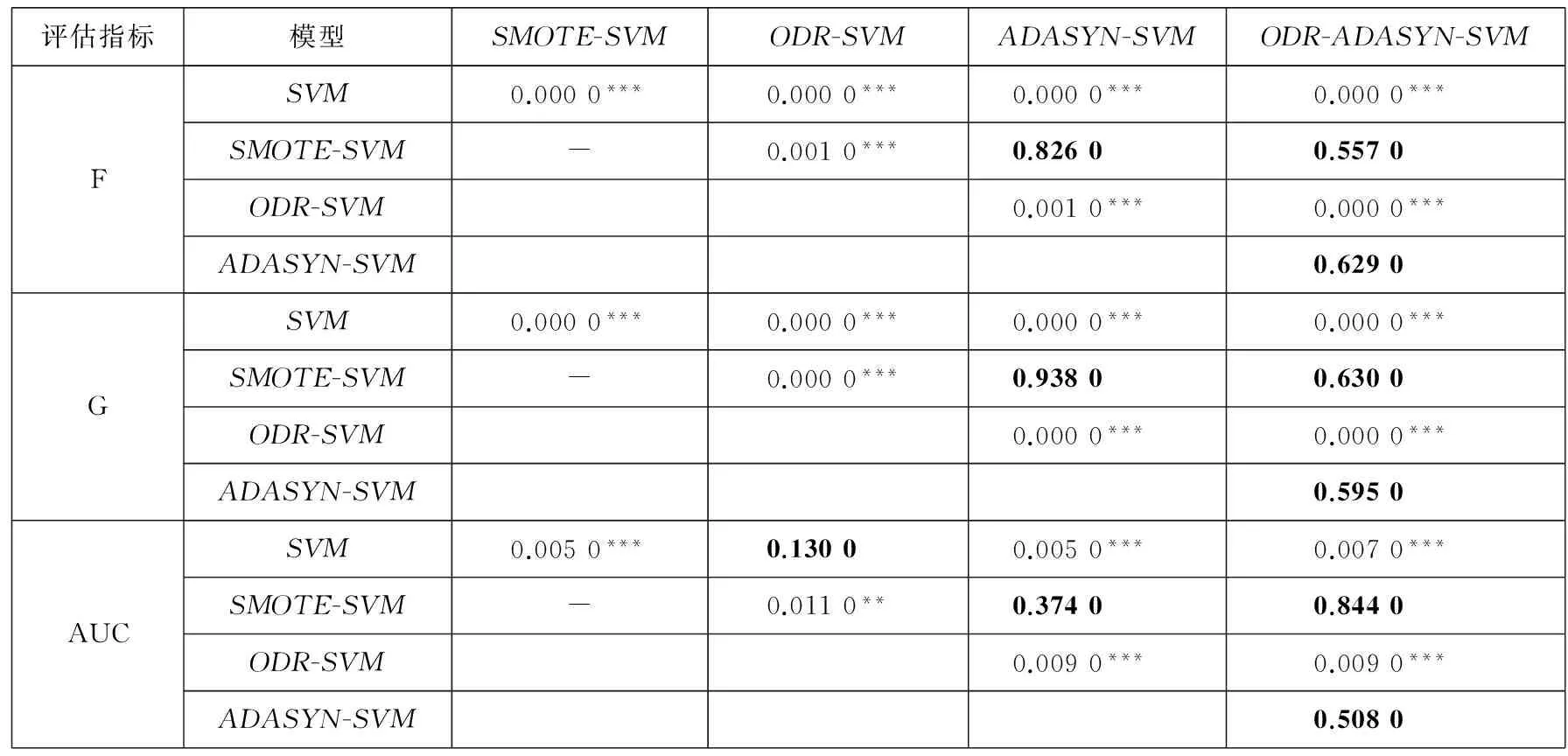
表6　模型预测性能的配对样本T检验结果

注：***表示p<0.01,**表示p<0.05, 加粗值表示p>0.1.

从表6可以看出，SVM与其余模型在G、F和AUC值上的绝大部分配对样本T检验统计量在1%的显著水平下拒绝零假设(nullhypothesis)，即SVM与其余模型的预测性能差异显著.由此表明，基于预测精度的角度，SVM模型的预测性能显著低于其余模型，从而证明了SMOTE、ODR、ADASYN以及ODR与ADASYN相结合的ODR-ADASYN能够提升SVM的非均衡样本学习能力.此外，从表6还可以看出，ODR-SVM与SMOTE-SVM、ADASYN-SVM、ODR-ADASYN-SVM模型的预测性能也存在显著差异，表明ODR-SVM模型的预测性能显著低于SMOTE-SVM、ADASYN-SVM和ODR-ADASYN-SVM模型的预测性能，由此可见，仅仅运用ODR来删除非极端金融风险样本中的噪声信息，以克服SMOTE在处理对象上存在的局限性，而不结合ADASYN来克服SMOTE在生成极端金融风险样本中的盲目性，并不能十分有效地提升SVM模型的预测性能.令人遗憾的是，从表6中无法观察到ODR-ADASYN-SVM模型与SMOTE-SVM、ADASYN-SVM模型的预测性能存在显著差异，因而也就无法充分证明ODR与ADASYN相结合在克服SMOTE的过拟合问题上具有显著优势.基于此，本文还将从预测稳定性的角度来继续探讨ODR-ADASYN-SVM模型较SMOTE-SVM和ADASYN-SVM模型的显著优越性.

为了对比ODR-ADASYN-SVM模型与SMOTE-SVM、ADASYN-SVM模型的预测稳定性，本文在设置与上述实验相同参数的基础上，通过修改极端金融风险样本的门槛值，将极端金融风险样本与非极端金融风险样本的比例分别设置为1∶5、1∶10、1∶15、1∶20、1∶25、1∶30、1∶35、1∶40、1∶45、1∶50这10个水平，进而对这10个水平下3类模型的预测精度变化情况进行分析，从而判定3类模型的预测稳定性，并最终挖掘出3类模型在预测性能上的显著差异.实验结果如图4和表7所示.

从图4可以看出，在各种非均衡比例下，ADASYN-SVM的G和AUC值几乎都高于SMOTE-SVM，并且ADASYN-SVM的波动幅度也小于SMOTE-SVM，而从表7也可以看出，不同非均衡比例下，ADASYN-SVM的G和AUC值的均值都大于SMOTE-SVM，并且ADASYN-SVM的G和AUC值的标准差也明显小于SMOTE-SVM，证明ADASYN-SVM的波动幅度明显小于SMOTE-SVM，从而说明在不同的非均衡比例下，ADASYN-SVM模型对两类样本共同预测的稳定性明显优于SMOTE-SVM模型.

更为重要是，图4还展示出ODR-ADASYN-SVM的G和AUC值几乎都高于ADASYN-SVM和SMOTE-SVM，并且ODR-ADASYN-SVM的波动幅度也最小，同时，从表7也可以看出，ODR-ADASYN-SVM的G和AUC值的均值都大于ADASYN-SVM和SMOTE-SVM，并且ODR-ADASYN-SVM的G和AUC值的标准差都低于0.05，明显小于ADASYN-SVM和SMOTE-SVM，表明ODR-ADASYN-SVM的波动幅度明显小于ADASYN-SVM和SMOTE-SVM，从而说明在不同的非均衡比例下，ODR-ADASYN-SVM模型在对两类样本的共同预测上具有最优的稳定性.

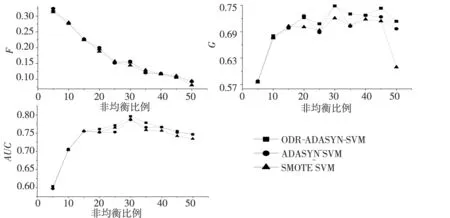
图4　不同非均衡比例下ODR-ADASYN-SVM、ADASYN-SVM和SMOTE-SVM的G、F和AUC值比较

注:不带括号外的值表示均值，带括号的值表示标准差.

然而，从图4却无法看出3类模型的F值在不同非均衡比例下的大小差异，也看不出各模型F值的波动幅度的差异.尽管通过表7能够看出在不同非均衡比例下，ODR-ADASYN-SVM的F值的均值大于ADASYN-SVM和SMOTE-SVM，ADASYN-SVM的F值的均值大于SMOTE-SVM，以及ODR-ADASYN-SVM的F值的标准差小于ADASYN-SVM和SMOTE-SVM，ADASYN-SVM的F值的标准差小于SMOTE-SVM，但大小差异都很不明显，因而无法判定3类模型在极端金融风险预测上稳定性的显著差异，也就更加无法展现3类模型的极端金融风险预测性能的显著差异.为了展现出3类模型的极端金融风险预测性能的显著差异性，本文还将对在不同非均衡比例下3类模型的F值进行独立样本T检验.实验结果见表8.

表8　不同非均衡比例下3类模型F值的独立样本T检验结果

注:未加括号的值表示ODR-ADASYN-SVM的p值, 加下划线的值表示ADASYN-SVM的p值, 而加有括号的值表示SMOTE-SVM的p值, *表示p<0.1,**表示p<0.05,***表示p<0.01, 加粗值表示p>0.1.

分析表8可知，ODR-ADASYN-SVM模型加粗的p值达到9个，带“***”的p值只有28个；ADASYN-SVM模型加粗的p值有8个，带“***”的p值有29个；而SMOTE-SVM模型加粗的p值只有6个，带“***”的p值却达到31个，说明在10%的显著水平下，ODR-ADASYN-SVM模型的F值在所有非均衡比例下接受零假设9次，ADASYN-SVM模型接受8次，SMOTE-SVM模型仅接受6次，而在1%的显著水平下，ODR-ADASYN-SVM模型的F值在所有非均衡比例下拒绝零假设仅28次，ADASYN-SVM拒绝29次，SMOTE-SVM模型却拒绝31次，从这个角度来说，ODR-ADASYN-SVM模型在各非均衡比例下的预测精度差异最不显著，其次是ADASYN-SVM模型，而最为显著的是SMOTE-SVM模型，从而说明，在不同的非均衡比例下，ODR-ADASYN-SVM模型对于极端金融风险样本预测的稳定性优于SMOTE-SVM模型和ADASYN-SVM模型，而ADASYN-SVM模型又优于SMOTE-SVM模型.

基于图4、表7与表8的分析，本文认为，尽管从预测精度分析，ODR-ADASYN-SVM的预测性能并不显著优于SMOTE-SVM和ADASYN-SVM，但从预测稳定性分析，ODR-ADASYN-SVM的预测性能显著优于SMOTE-SVM和ADASYN-SVM，而ADASYN-SVM却又显著优于SMOTE-SVM，从而证明了ADASYN能够有效地克服SMOTE在生成极端金融风险样本中的盲目性，但仅仅运用ADASYN并不能最为有效地提升SVM模型的预测性能，只有将ODR与ADASYN相结合来克服SMOTE存在的过拟合，才能促使SVM模型的性能提升达到最为优异的效果.

综上所述，参数K对ODR-ADASYN-SVM模型的预测性能影响不大，而参数α却对ODR-ADASYN-SVM模型的预测性能有着较大的影响.因此，通过对参数α的调整，就能够得到最优的ODR-ADASYN-SVM预警模型.并且无论是从预测精度分析，该模型的预测性能显著优于SVM和ODR-SVM模型，还是从预测稳定性分析，该模型也显著优于SMOTE-SVM和ADASYN-SVM模型，从而充分证明了将ODR与ADASYN相结合不仅能够提升SVM的非均衡样本学习能力，而且比单独运用ODR和ADASYN来克服SMOTE的过拟合能够取得更加优异的效果.从上述分析可知，由ODR、ADASYN和SVM结合成ODR-ADASYN-SVM模型，能够较好地预测中国极端金融风险，从而为金融经济管理部门和投资者应对与防范极端金融风险提供了有效的操作工具.

3结束语

本文以CSI300指数为研究对象，运用EVT理论确定出极端与非极端金融风险样本，并运用统计假设检验和逐步判别分析法提取市场内部特征指标以及运用ClaytonCopula方法提取市场外部特征指标，进而引入ADASYN来克服SMOTE在生成新样本中的盲目性；针对SMOTE在处理对象上的局限性，还引入ODR来删除非极端金融风险样本中的噪声信息；并与SVM相结合，构造了改进SVM，即ODR-ADASYN-SVM模型，并对该模型的最邻近参数K和ODR的参数α进行讨论，进而运用最优的ODR-ADASYN-SVM模型来预测中国极端金融风险，然后再运用性能评估指标对SVM、SMOTE-SVM、ODR-SVM、ADASYN-SVM以及ODR-ADASYN-SVM模型的预测精度进行评估，并最终运用T检验对各模型预测精度的差异性进行显著性检验以及对各模型的预测稳定性进行评价.实证结果表明，无论是从预测精度分析，ODR-ADASYN-SVM模型的预测性能显著优于SVM和ODR-SVM模型，还是从预测稳定性分析，ODR-ADASYN-SVM模型也显著优于SMOTE-SVM和ADASYN-SVM模型，从而说明ODR-ADASYN方法能够成功地克服SMOTE的过拟合，并有效地提升SVM的非均衡样本学习能力，同时，ODR-ADASYN-SVM预警模型在中国极端金融风险预测上具有最为优越的预测性能.

本文的研究能够为金融经济管理部门和投资者应对与防范极端金融风险提供可操作性的应用工具与方法.对于金融经济管理部门而言，能够运用ODR-ADASYN-SVM模型对未来一段时间内的金融市场极端风险进行准确预测，及时制定并实施应对金融风险危机的相关宏观经济政策，从而构建金融市场极端风险危机的“防火墙”，积极地化解与防范金融风险危机，以维护金融市场稳定，促进经济持续健康发展；对于投资者而言，能够运用ODR-ADASYN-SVM模型提前捕获金融市场风险危机信号，进而即时调整金融资产投资策略，以优化金融资产投资组合，从而更为有效地管理金融资产，保证金融资产的保值甚至增值.

本文提出的风险预警方法，虽然丰富了市场主体对极端金融风险预警的研究手段，但仍需要指出的是，金融市场样本除存在极端与非极端两种分类状态外，也存在多分类状态，运用本文提出的风险预警模型将无法进行多分类研究.因此，如何改进SVM方法，并结合非均衡样本处理方法进行多分类状态下的极端金融风险预警研究，将是下一步的主要研究方向.

参 考 文 献：

[1]魏宇. 股票市场的极值风险测度及后验分析研究[J]. 管理科学学报, 2008, 11(1): 78-88.

WeiYu.EVTriskmeasuresanditsbacktestinginstockmarkets[J].JournalofManagementSciencesinChina, 2008, 11(1): 78-88. (inChinese)

[2]FrankelJA,RoseAK.Currencycrashesinemergingmarkets:Anempiricaltreatment[J].JournalofInternationalEconomics, 1996, 41(3/4): 351-366.

[3]SachsJ,TornellA,VelascoA.Financialcrisesinemergingmarkets:Thelessonsfrom1995[J].BrookingsPapersonEconomicActivity, 1996, 27(1): 147-215.

[4]KaminskyG,LizondoS,ReinhartCM.LeadingIndicatorsofCurrencyCrises[R].IMFStaffPaper, 1998, 45(1): 1-48.

[5]陈守东, 杨莹, 马辉. 中国金融风险预警研究[J]. 数量经济技术经济研究, 2006, (7): 36-48.

ChenShoudong,YangYing,MaHui.Thestudyofearly-warningonChinesefinancialrisk[J].TheJournalofQuantitative&TechnicalEconomics, 2006, (7): 36-48. (inChinese)

[6]KimTY,OhKJ,SohnI,etal.Usefulnessofartificialneuralnetworksforearlywarningsystemofeconomiccrisis[J].ExpertSystemswithApplications, 2004, 26(4): 583-590.

[7]周敏, 王新宇. 基于模糊优选和神经网络的企业财务危机预警[J]. 管理科学学报, 2002, 5(3): 86-90.

ZhouMin,WangXinyu.Pre-warningsystemsofenterprisefinancialcrisisbasedonfuzzyselectionandartificialneuralnetworks[J].JournalofManagementSciencesinChina, 2002, 5(3): 86-90. (inChinese)

[8]VapnikVN.TheNatureofStatisticalLearningTheory[M].NewYork:Springer-Verlag, 1995.

[9]LiH,SunJ.Forecastingbusinessfailure:Theuseofnearest-neighboursupportvectorsandcorrectingimbalancedsamples-evidencefromtheChinesehotelindustry[J].TourismManagement, 2012, 33(3): 622-634.

[10]MarateaA,PetrosinoA,MarioM.AdjustedF-measureandkernelscalingforimbalanceddatalearning[J].InformationSciences, 2014, 257(1): 331-341.

[11]SundarkumarGG,RaviV.Anovelhybridundersamplingmethodforminingunbalanceddatasetsinbankingandinsurance[J].EngineeringApplicationsofArtificialIntelligence, 2015, 37(1): 368-377.

[12]ChawlaN,BowyerK,HallL,etal.SMOTE:Syntheticminorityover-samplingtechnique[J].JournalofArtificialIntelligenceResearch, 2002, (16): 321-357.

[13]WangBX,JapkowiczN.Imbalanceddatasetlearningwithsyntheticsamples[C]//Proc.IRISMachineLearningWorkshop, 2004: 1-25.

[14]HeH,BaiY,GarciaEA,etal.ADASYN:Adaptivesyntheticsamplingapproachforimbalancedlearning[C]//Proc.Int’lJ.Conf.NeuralNetworks, 2008: 1322-1328.

[15]陶新民, 童智靖, 刘玉, 等. 基于ODR和BSMOTE结合的不均衡数据SVM分类算法[J]. 控制与决策, 2011, 26(10): 1535-1541.

TaoXinmin,TongZhijing,LiuYu,etal.SVMclassifierforunbalanceddatabasedoncombinationofODRandBSMOTE[J].ControlandDecision, 2011, 26(10): 1535-1541. (inChinese)

[16]戴文华, 夏峰. 关于中国证券市场20年发展的基本分析与思考[J]. 证券市场导报, 2014, (1): 4-11.

DaiWenhua,XiaFeng.Thebasicanalysisandreflectionsonthe20yearsofdevelopmentofthesecuritiesmarket[J].SecuritiesMarketHerald, 2014, (1): 4-11. (inChinese)

[17]黄金波, 李仲飞, 姚海洋. 基于CVaR核估计量的风险管理[J]. 管理科学学报, 2014, 17(3): 49-59.

HuangJinbo,LiZhongfei,YaoHaiyang.RiskmanagementbasedontheCVaRkernelestimator[J].JournalofManagementSciencesinChina, 2014, 17(3): 49-59. (inChinese)

[18]熊熊, 张珂, 周欣. 国际市场对我国股票市场系统性风险的影响分析[J]. 证券市场导报, 2015, (1): 54-58.

XiongXiong,ZhangKe,ZhouXin.AnalysisofimpactofinternationalmarketonChinastockmarketsystemicrisk[J].SecuritiesMarketHerald, 2015, (1): 54-58. (inChinese)

[19]吴勇民, 纪玉山, 吕永刚. 技术进步与金融结构的协同演化研究——来自中国经验证据[J]. 现代财经(天津财经大学学报), 2014, (7): 33-44.

WuYongmin,JiYushan,LüYonggang.Studyontheco-evolutionoftechnologicalprogressandfinancialstructure:TheempiricalevidencefromChina[J].ModernFinanceandEconomics(JournalofTianjinUniversityofFinanceandEconomics), 2014, (7): 33-44. (inChinese)

[20]AhnJJ,OhKJ,KimDH.Usefulnessofsupportvectormachinetodevelopanearlywarningsystemforfinancialcrisis[J].ExpertSystemswithApplications, 2011, 38(4): 2966-2973.

[21]GrothSS,MuntermannJ.Anintradaymarketriskmanagementapproachbasedontextualanalysis[J].DecisionSupportSystems, 2011, 50(4): 680-691.

[22]徐国祥, 杨振建.PCA-GA-SVM模型的构建及应用研究——沪深300指数预测精度实证分析[J]. 数量经济技术经济研究, 2011, (2): 135-147.

XuGuoxiang,YangZhenjian.ResearchforconstructionandapplicationofPCA-GA-SVMmodel[J].TheJournalofQuantitative&TechnicalEconomics, 2011, (2): 135-147. (inChinese)

[23]李云飞, 惠晓峰. 基于支持向量机的股票投资价值分类模型研究[J]. 中国软科学, 2008, (1): 135-140.

LiYunfei,HuiXiaofeng.TheclassificationmodelforstockinvestmentvaluebasedonSVM[J].ChinaSoftScienceMagazine, 2008, (1): 135-140. (inChinese)

[24]FarquadMAH,IndranilB.Preprocessingunbalanceddatausingsupportvectormachine[J].DecisionSupportSystems, 2012, 53(1): 226-233.

[25]HuangZ,ChenHC,HsuCJ,etal.Creditratinganalysiswithsupportvectormachinesandneuralnetworks:Amarketcomparativestudy[J].DecisionSupportSystems, 2004, 37 (4): 543-558.

[26]宋新平, 丁永生. 基于最优支持向量机模型的经营失败预警研究[J]. 管理科学, 2008, 21(1): 115-121.

SongXinping,DingYongsheng.Studyonbusinessfailurepredictionbasedonanoptimizedsupportvectormachinemodel[J].JournalofManagementSciences, 2008, 21(1): 115-121. (inChinese)

[27]邹鹏, 李一军, 郝媛媛. 基于代价敏感性学习的客户价值细分[J]. 管理科学学报, 2009, 12(1): 48-56.

ZouPeng,LiYijun,HaoYuanyuan.Customervaluesegmentationbasedoncost-sensitivelearning[J].JournalofManagementSciencesinChina, 2009, 12(1): 48-56. (inChinese)

[28]魏宇, 赖晓东, 余江. 沪深300股指期货日内避险模型及效率研究[J]. 管理科学学报, 2013, 16(3): 29-40.

WeiYu,LaiXiaodong,YuJiang.Intra-dayhedgingmodelsandhedgingeffectivenessofCSI300indexfutures[J].JournalofManagementSciencesinChina, 2013, 16(3): 29-40. (inChinese)

[29]陈莹, 武志伟, 王杨. 沪深300指数衍生证券的多市场交易与价格发现[J]. 管理科学学报, 2014, 17(12): 75-84.

ChenYing,WuZhiwei,WangYang.Multi-markettradingofHS300indexderivativesandpricediscoveryofstockmarketindex[J].JournalofManagementSciencesinChina, 2014, 17(12): 75-84. (inChinese)

[30]HillBM.Asimplegeneralapproachtoinferenceaboutthetailofadistribution[J].TheAnnalsofStatistics, 1975, 3(5): 1163-1174.

[31]SteliosDB,DimitrisAG.EstimationofValue-at-Riskbyextremevalueandconventionalmethods:Acomparativeevaluationoftheirpredictiveperformance[J].Int.Fin.Markets,Inst.andMoney, 2005, 15 (3): 209-228.

[32]NeftciS.Valueatriskcalculations,extremeeventsandtailestimation[J].TheJournalofDerivations, 2000(Spring), 7(3): 23-37.

[33]DuMouchelWH.Estimatingthestableindexαinordertomeasuretailthickness:Acritique[J].AnnalsofStatistics, 1983, 11(4): 1019-1031.

[34]KimotoT,AsakawaK.Stockmarketpredictionsystemwithmodularneuralnetworks[C]//Proc.Int’lJ.Conf.NeuralNetwork, 1990: 1-6.

[35]叶五一, 缪柏其. 基于Copula变点检测的美国次级债金融危机传染分析[J]. 中国管理科学, 2009, 17(3): 1-7.

YeWuyi,MiaoBaiqi.Analysisofsub-primeloancrisiscontagionbasedonchangepointtestingmethodofCopula[J].ChineseJournalofManagementScience, 2009, 17(3): 1-7. (inChinese)

[36]王永巧, 刘诗文. 基于时变Copula的金融开放与风险传染[J]. 系统工程理论与实践, 2011, 31(4): 778-784.

WangYongqiao,LiuShiwen.Financialmarketopennessandriskcontagion:Atime-varyingCopulaapproach[J].SystemsEngineering-Theory&Practice, 2011, 31(4): 778-784. (inChinese)

[37]叶五一, 韦伟, 缪柏其. 基于非参数时变Copula模型的美国次贷危机传染分析[J]. 管理科学学报, 2014, 17(11): 151-158.

YeWuyi,WeiWei,MiaoBaiqi.Analysisofsub-primeloancrisiscontagionbasedonnon-parametrictime-varyingCopula[J].JournalofManagementSciencesinChina, 2014, 17(11): 151-158. (inChinese)

[38]宋新平, 丁永生, 曾月明. 基于遗传算法的同步优化方法在财务困境预警中的应用[J]. 预测, 2009, 28(1): 48-55.

SongXinping,DingYongsheng,ZengYueming.ApplicationofaGA-basedsimultaneousoptimizationmethodinfinancialcrisisprediction[J].Forecasting, 2009, 28(1): 48-55. (inChinese)

EarlywarningforextremelyfinancialrisksbasedonODR-ADASYN-SVM

LIN Yu1, HUANG Xun1, CHUN Wei-de1, HUANG Deng-shi2

1.BusinessSchool,ChengduUniversityofTechnology,Chengdu610059,China;2.SchoolofEconomicsandManagement,SouthwestJiaotongUniversity,Chengdu610031,China

Abstract:Synthetic minority over-sampling technique (SMOTE)has the problem of over fitting in improving the imbalanced samples’ learning ability of support vector machine (SVM). In this paper, adaptive synthetic sampling approach (ADASYN) and optimization of decreasing reduction approach (ODR) are assembled into an ODR-ADASYN to overcome the blindness in generating new samples and the limitations in processing the object. Combining SVM with ODR-ADASYN, an improved SVM, named ODR-ADASYN-SVM, is put forward to predict extremely financial risks; T-test is also applied to the significance test of the difference of the prediction accuracy of all models and to the evaluation of the prediction stability of all models. The result illustrates that the ODR-ADASYN-SVM can not only significantly improve the imbalanced samples’ learning ability of SVM, but also overcome the problem of over fitting for SMOTE effectively.Hence, the ODR-ADASYN-SVM has a superior ability to predict extremely financial risks.

Key words:ODR; ADASYN; SVM; extremely financial risk; early warning model

收稿日期:①2013-06-07；

修订日期:2015-07-13.

基金项目:国家自然科学基金资助项目(71171025)； 国家社会科学基金资助项目(12BGL024)； 四川省软科学研究计划资助项目(2014ZR0093)； 成都理工大学“金融与投资”优秀创新团队计划资助项目(KYTD201303).

作者简介:林宇(1973—)， 男， 四川仪陇人， 博士， 教授. Email:linyuphd@126.com

中图分类号:F832.5

文献标识码:A

文章编号:1007-9807(2016)05-0087-15