一类含迭代的二元均值函数

陈荔靖

(四川大学数学学院,成都 610064)

1 引 言

均值是统计学中最常用的统计量，常被用来描述统计对象总体的一般水平或分布的集中趋势，柯西[1]首先给出了均值函数的定义：设区间I⊂R，若对任意x,y∈I，函数M:I2→R满足

min(x,y)≤M(x,y)≤max(x,y),

则称M是I2上的均值函数. 若上述不等式等号成立当且仅当x=y，则称M是I2上的严格均值函数.显然，均值函数具有自反性，即对任意x∈I，M(x,x)=x.设K,M,N:I2→I都是均值函数，若对任意x,y∈I,M(x,y)=M(y,x)，则称M是对称的；若对任意x,y∈I,K满足

K(M(x,y),N(x,y))=K(x,y),

则称K关于(M,N)是不变的.设M2(I)是定义在区间I上的一类二元均值函数，若M,N∈M2(I)，并且对任意x,y∈I有M(x,y)=N(x,y)，则称M,N等价.

经典的均值函数有算术均值函数A:R2→R:

(1)

几何均值函数G:(0,+∞)2→(0,+∞):

(2)

以及调和均值函数H:(0,+∞)2→(0,+∞):

(3)

它们都具有对称性，且满足G∘(A,H)=G.

1930年，Kolmogoroff[2]引入了拟算术均值函数的形式定义.设区间I⊂R,φ:I→R连续且严格单调，称

(4)

为拟算术均值函数.式(1)～(3)中的函数都是拟算术均值函数的特殊形式.此后，Hardy等[3]研究了拟算术均值函数的等价性，Matkowski[4]研究了算术均值函数关于拟算术均值函数的不变性.

当(4)式中的等权重1/2变为不等权重p∈(0,1)和1-p时，(4)式变为加权拟算术均值函数.Daróczy[5]研究了有关该类均值函数的函数方程，在加权拟算术均值函数中的权重为权重函数时得到带有权重函数的拟算术均值函数.Jarczyk[6]研究了带有权重函数的拟算术均值函数关于这一类均值函数的不变性.

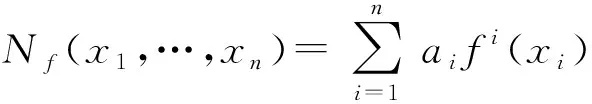
Nf(x,y)=a1f(x)+a2f2(y)

(5)

研究了算术均值函数、拟算术均值函数关于该类均值函数的不变性.

受上述工作启发，本文研究式(5)的推广形式

Mf(x,y)=λ1f(x)+λ2f2(x)+

μ1f(y)+μ2f2(y)

(6)

我们首先给出Mf为均值函数的条件，进而研究了Mf的对称性、等价性及拟算术均值函数关于该类均值函数的不变性.

2 预备知识

[HTH][STHZ]引理2.1[HT][ST][WT] 设区间I⊂R,f:I→I连续，λ1,λ2,μ1,μ2∈R. 若对任意x,y∈I,Mf是均值函数，则

(i) 对任意x∈I,有

(λ1+μ1)f(x)+(λ2+μ2)f2(x)=x

(7)

并且λ1,λ2,μ1,μ2不全为0，f是单射；

(ii) 当λ2+μ2≠0时，对任意x∈I,

(8)

若此时λ1μ2-λ2μ1=0，则对任意x,y∈I,

(9)

当λ2+μ2=0时，对任意x,y∈I,

(10)

(iii)λ1f+λ2f2,μ1f+μ2f2均单增.

[HTK]证明[HT] (i) 由均值函数的自反性可知，对任意x∈I,(7)式成立. 若λ1,λ2,μ1,μ2全为0，则对任意x,y∈I，Mf(x,y)=0，与Mf为均值函数矛盾. 若存在x,y∈I，使得f(x)=f(y)，则f2(x)=f2(y).所以

x=Mf(x,x)=

(λ1+μ1)f(x)+(λ2+μ2)f2(x)=

(λ1+μ1)f(y)+(λ2+μ2)f2(y)=

Mf(y,y)=y.

因此f是单射.

(ii) 当λ2+μ2≠0时，由(7)式易知,对任意x∈I，(8)式成立. 若此时λ1μ2-λ2μ1=0，将(8)式代入(6)式计算可得， 对任意x,y∈I,(9)式成立.

当λ2+μ2=0时，由(7)式可得，对任意x∈I,(λ1+μ1)f(x)=x,故此时λ1+μ1≠0. 因此，对任意x∈I,

(10)式成立.

(iii) 由均值函数的自反性知Mf(y,y)=y， 所以对任意y∈I,

μ1f(y)+μ2f2(y)=y-λ1f(y)-λ2f2(y).

因此，

Mf(x,y)=λ1f(x)+λ2f2(x)+y-

λ1f(y)-λ2f2(y)

(11)

由均值函数的定义可知，对任意x,y∈I,

min(x,y)≤λ1f(x)+λ2f2(x)+y-λ1f(y)-

λ2f2(y)≤max(x,y)

所以λ1f+λ2f2单增. 同理可得μ1f+μ2f2单增. 证毕.

3 主要结果及证明

[HTH][STHZ]定理 3.1[HT][ST][WT] 设区间I⊂R,f:I→I连续，λ1,λ2,μ1,μ2∈R，则下列等价：

(i) 对任意x,y∈I,Mf是均值函数；

(ii) 对任意x∈I,(7)式成立， 且λ1f+λ2f2,μ1f+μ2f2均单增.

[HTK]证明[HT] 假设(i)成立.由引理2.1的(i)、(iii)可得，(ii)成立.

若(ii)成立，则对任意x∈I,Mf(x,x)=x，并且对任意x,y∈I有

min(x,y)=λ1f(min(x,y))+

λ2f2(min(x,y))+μ1f(min(x,y))+

μ2f2(min(x,y))≤λ1f(x)+λ2f2(x)+

μ1f(y)+μ2f2(y)≤λ1f(max(x,y))+

λ2f2(max(x,y))+μ1f(max(x,y))+

μ2f2(max(x,y))=max(x,y)

(12)

因此Mf是均值函数. 证毕.

[HTH][STHZ]定理 3.2[HT][ST][WT] 设区间I⊂R,f:I→I连续，λ1,λ2,μ1,μ2∈R，则下列等价：

(i) 对任意x,y∈I,Mf是严格均值函数;

(ii) 对任意x∈I,(7)式成立，λ1,λ2不全为0且μ1,μ2不全为0，λ1f+λ2f2,μ1f+μ2f2均严格单增.

[HTK]证明[HT] 设(i)成立.则λ1,λ2不全为0且μ1,μ2不全为0. 事实上，若λ1=λ2=0，此时必有μ1,μ2不全为0，则对任意x,y∈I,

Mf(x,y)=μ1f(y)+μ2f2(y)=

Mf(y,y)=y.

这与Mf是严格均值函数矛盾. 同理，若μ1=μ2=0，易推出矛盾.

若存在x,y∈I，使得

λ1f(x)+λ2f2(x)=λ1f(y)+λ2f2(y),

则由均值函数的自反性可知(11)式成立.所以此时Mf(x,y)=y. 又因Mf是严格均值函数，故x=y. 因而λ1f+λ2f2是单射. 同理μ1f+μ2f2也是单射. 再由定理3.1知(ii)成立.

若(ii)成立，将(12)式中“≤”替换为“<”即得证. 证毕.

[HTH][STHZ]定理 3.3[HT][ST][WT] 设区间I⊂R,λ1,λ2,μ1,μ2∈R,f:I→I连续， 对任意x,y∈I,Mf是均值函数.Mf是对称的当且仅当

(13)

[HTK]证明[HT] 必要性.若Mf是对称的，则对任意x,y∈I,Mf(x,y)=Mf(y,x). 因此，

(λ1-μ1)f(x)+(λ2-μ2)f2(x)=

(λ1-μ1)f(y)+(λ2-μ2)f2(y).

从而存在C∈R，使得对任意x∈I,

(λ1-μ1)f(x)+(λ2-μ2)f2(x)=C

(14)

当λ2+μ2≠0时，因为Mf是均值函数， 由引理2.1的(ii)可知，对任意x,y∈I,(8)式成立. 将(8)式代入(14)式可得

(15)

若λ1μ2-λ2μ1≠0，由(15)式可知，对任意x,y∈I,

(16)

其中

此时一定有λ2≠μ2，否则f为常数与引理2.1(i)中的f是单射矛盾.将(8)，(16)式代入(6)式计算可得(13)式成立.

若λ1μ2-λ2μ1=0，则由引理2.1的(ii)可知(9)式成立. 又由Mf对称得λ2=μ2,所以(13)式成立.

当λ2+μ2=0时，由引理2.1的(ii)可得,对任意x,y∈I,(10)式成立. 因此，由均值函数的自反性Mf(x,x)=x知

(17)

再由Mf具有对称性可得

(18)

所以(13)式成立.

充分性.若(13)式成立,则显然有Mf(x,y)=Mf(y,x). 证毕.

为讨论方便，以下记

μ1f(y)+μ2f2(y)

(19)

(20)

易见Mf=Mf,Λ.

(21)

(22)

[HTK]证明[HT] 必要性. 若Mf,Λ,Mg,Λ′都是均值函数， 由均值函数的自反性可知，对任意x,y∈I,Mf,Λ(x,y)=Mg,Λ′(x,y)意味着

λ1f(x)+λ2f2(x)+y-λ1f(y)-λ2f2(y)=

故此时存在C∈R，使得对任意x∈I，(21)式成立. 同理可得存在C′∈R，使得对任意x∈I，(22)式成立. 又由于对任意x,y∈I,

Mf,Λ(x,y)-Mg,Λ′(x,y)=

(23)

因此C+C′=Mf,Λ(x,y)-Mg,Λ′(x,y)=0.

充分性.反过来，由(23)式及条件易得， 对任意x,y∈I,Mf,Λ(x,y)=Mg,Λ′(x,y). 证毕.

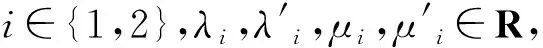
若由(19)，(20)式定义的Mf,Λ,Mg,Λ′都是均值函数，则

(i) 拟算术均值函数Aφ关于(Mf,Λ,Mg,Λ′)是不变的，即

Aφ∘(Mf,Λ,Mg,Λ′)=Aφ

(24)

当且仅当对任意x,y∈I,

φ(Mf,Λ(x,y))+φ(Mg,Λ′(x,y))=

φ(x)+φ(y)

(25)

(ii) 若φ,f,g可导，对任意x∈I,φ′(x)≠0,Λ′=Λ，并且

Aφ∘(Mf,Λ,Mg,Λ)=Aφ

(26)

则λ1,λ2不全为0且μ1,μ2不全为0，对任意x,y∈I,有

Mg,Λ(x,y)=Mf,Λ(y,x)

(27)

并且当λ2+μ2≠0且λ1μ2-λ2μ1=0， 或当λ2+μ2=0时， 存在k,l∈R且k≠0，使得

φ(x)=kx+l

(28)

[HTK]证明[HT] (i) 显然成立.

(ii) 由于Λ′=Λ，则

Mg,Λ(x,y)=λ1g(x)+λ2g2(x)+

μ1g(y)+μ2g2(y)

(29)

因为(26)式成立，所以由(i)可知，

φ(Mf,Λ(x,y))+φ(Mg,Λ(x,y))=

φ(x)+φ(y)

(30)

若λ1=λ2=0，此时必有μ1,μ2不全为0.则由均值函数的自反性可知，对任意x,y∈I,

Mf,Λ(x,y)=y=Mg,Λ(x,y)

(31)

将(31)式代入(30)式可得，对任意x,y∈I,φ(x)=φ(y).则φ为常函数，与φ严格单调矛盾. 同理， 若μ1=μ2=0可推出矛盾. 因此λ1,λ2不全为0且μ1,μ2不全为0.

当λ2+μ2≠0时，由引理2.1的(ii)可知， 对任意x∈I，(8)式成立，且

(32)

将(8),(32)式分别代入(19),(29)式后对x求导可得

(33)

对(30)式左右两边x求导可得

(34)

将(33)式代入(34)式，再令y=x，由对 任意x∈I,Mf,Λ(x,x)=Mg,Λ(x,x)=x,φ′(x)≠0可知，

(35)

若λ1μ2-λ2μ1≠0，则由(35)式可知， 存在c∈R，使得

(36)

将(32),(36)式代入(29)式计算可得

Mg,Λ(x,y)=

λ1f(y)+λ2f2(y)+μ1f(x)+μ2f2(x)=

Mf,Λ(y,x).

若λ1μ2-λ2μ1=0，由引理2.1的(ii)可知， 对任意x,y∈I,(9)式成立.所以此时Mf,Λ(x,y)=Mg,Λ(x,y)=Mf(x,y). 又由(35)式可得λ2=μ2.所以

(37)

故对任意x,y∈I,(27)式成立. 由(30)式，此时

(38)

为Jensen方程. 又因为φ连续且严格单调，由文献[9]可知， 存在k,l∈R且k≠0，使得(28)式成立.

当λ2+μ2=0时，由引理2.1的(ii)可知(10)式成立. 所以此时Mf,Λ(x,y)=Mg,Λ(x,y)=Mf(x,y). 由(30)式，

(39)

(40)

同时对(40)式左右两边x求导可得φ′(x)=0.这与φ严格单调矛盾. 由文献[9]知

因此(37)式成立.从而对任意x,y∈I,(27)式成立. 再由(39)式知(38)式成立. 所以存在k,l∈R且k≠0，使得(28)式成立. 证毕.