声阻抗对盾构注浆冲击回波规律的影响研究

苏建洪，姚菲

(河海大学 土木与交通学院，江苏 南京 210098)

声阻抗对盾构注浆冲击回波规律的影响研究

苏建洪，姚菲

(河海大学 土木与交通学院，江苏 南京 210098)

摘要:基于盾构中管片-注浆-围岩模型和分层结构中材料声阻抗的相对值对冲击回波测试结果有较大影响的原理，利用大型有限元软件MSC.MARC建立4组(8种)不同注浆层与围岩材料参数的SGS(管片-注浆-围岩)模型，进行瞬态冲击数值模拟，研究不同声阻抗值对SGS模型冲击回波规律的影响。研究结果表明：注浆层声阻抗的大小对回波特性影响极大，其与管片声阻抗的相对值决定了所能探测到的界面，以及频域图上峰值频率的显著性。

关键词：声阻抗；SGS模型；冲击回波法；数值模拟

冲击回波无损检测技术使用瞬时应力波来探测物体内部的缺陷。20世纪80年代MarySansalon等[1]为了检测板状结构首先提出了这种方法, 如今它已被应用于很多土木结构的检测。主要包括板状结构(如桥面、混凝土路面和墙体)、梁和柱、层状物、柱状物以及预应力孔道注浆质量[2-4]等。随着城市地下空间开发与利用的发展，盾构施工技术越来越多地应用于城市的地铁隧道以及市政隧道工程中。在工程中采用壁后注浆技术，可以充填由于盾构刀盘外径大于隧道管片外径造成的超挖空隙，而且能够防止围岩松动、管片漏水、显著减少地面沉降，盾构管片壁后注浆质量对衬砌上土压力分布与地表沉降有重要影响[5]。注浆质量缺陷作为一种不外露缺陷，其检测方法成为一个急需的研究新领域，其中冲击回波法成为一个值得研究的新方向。

1基本原理

冲击回波法是利用瞬时机械冲击(用一个小钢球或小锤轻敲被测物表面)产生的低频应力波来对结构内部进行探测的。这些波遇到声阻抗有差异的介质界面就会发生反射、折射或绕射，不同界面之间的来回反射就会产生瞬态共振，再由放置在冲击点附近的传感器接收共振引起的位移信号。通过快速傅里叶变换(FFT)，将采集到的时域信号转化为频域信号，用于确定内部缺陷的深度和构件的厚度。

对于由2种或2种以上材料组成的分层结构，其材料的声阻抗值对冲击回波测试结果尤为重要。当应力波穿透2种不同声阻抗材质组成的界面时，一部分入射应力波会被反射回来，另一部分入射应力波会被折射进入下一介质中。反射波和折射波与入射波之间的关系如下[6]：

(1)

(2)

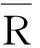
由式(1)和式(2)可知，反射系数的正负依赖于2种材料声阻抗的对比值。当Z1>Z2，则反射系数为负，意味着应力波反射后相位发生改变，此时反射波对应的传播频率f1(即介质1的厚度频率)的计算公式如下：

(3)

式中:β为形状系数，对于板取0.96；Cp1为介质1中的P波波速；T1为介质1的厚度。

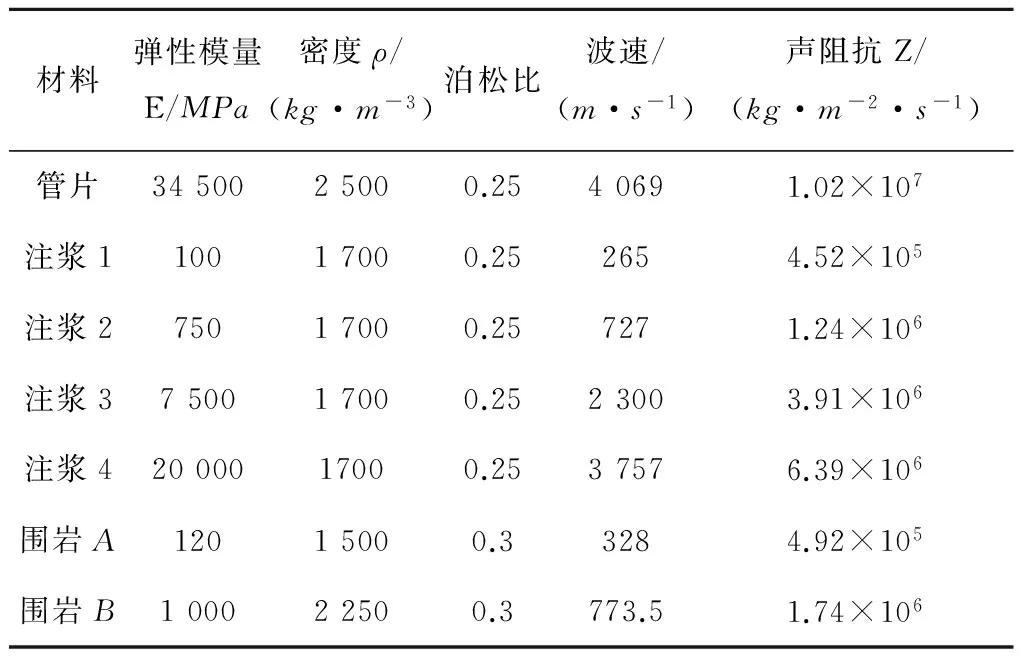
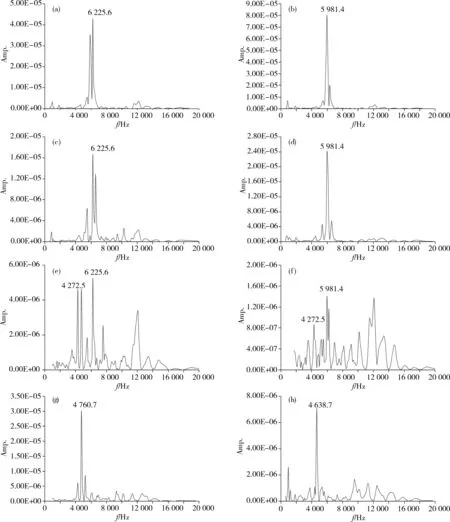
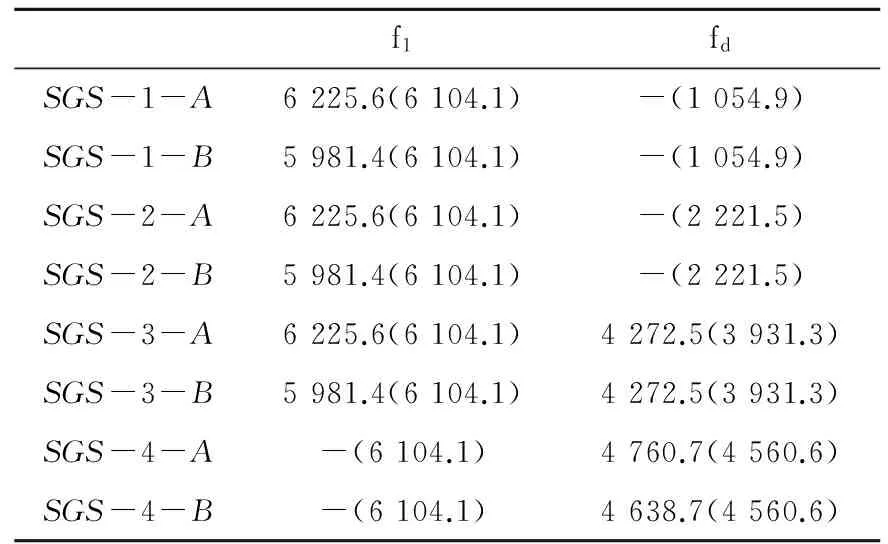
当Z1

(4)

式(3)与式(4)表明，介质声阻抗的相对值决定了厚度频率的计算公式。此外，由式(1)和式(2)也可知，2种材料声阻抗的不同也决定了界面上反射波的能量大小，从而决定了用冲击回波法能否探测到该界面。因而对于分层结构，材料声阻抗的相对值对冲击回波测试结果有非常大的影响。

在管片-注浆-土体(Segment-Grouting-Surroundingrock，以下简称SGS)模型中，注浆层材料的声阻抗值小于管片声阻抗，即属于Z1>Z2情况。但注浆层的具体声阻抗值随着材料配比的不同存在很大差别。此外，SGS模型中存在3层结构，围岩的力学性质也存在不确定性，注浆层-围岩界面可能会对回波信号产生影响。

注浆层-围岩界面相对应的厚度频率fd根据下式计算：

(5)

式中:T1和T2分别为混凝土管片与注浆层的厚度，Cp1和Cp2分别为混凝土管片与注浆层中的应力波波速。

2数值模型建立

基于本文的研究目的，模型的主要变量为材料声阻抗的相对值。因此设计4种注浆层材料参数，2种围岩参数，包括8种参数组合。将主要材料参数列于表1，参数组合列于表2。

表1　材料参数

表2　参数组合

采用大型有限元软件MSC.MARC完成模型的建立与计算。其中管片层厚度为320mm，注浆层厚度为100mm。采用平面分析方法，采用11号二维平面集成单元，以激励点为原点，激励方向线为对称轴，建立SGS模型。在边界单元处设置高阻尼以消除边界反射对结果的影响。将激振力最大值和激振时间分别定为8N和40μs，总分析时间为0.008s，时间步长4×10-6s。

图2　SGS有限元模型Fig.2 Finite element model of SGS

3计算结果分析

选取距离激励点8cm处节点，提取该处加速度、速度、位移时程曲线。以模型SGS-2-A为例，其速度时程曲线如图3(a)所示。为消除瑞利波的影响，实际处理后的曲线为截去了瑞利波的部分，如图3(b)所示。其余模型作类似处理，在此不再赘述。

(a)原时程曲线;(b)去除瑞利波后时程曲线图3　SGS-2-A速度时程曲线Fig.3 Velocity Time-history curve of SGS-2-A

将去除瑞利波后对时程曲线作FFT变换，获得对应的频域图，如图4所示。

图4　SGS-2-A频域图Fig.4 Frequency domain of SGS-2-A

由图4可见，除了在厚度频率有效区域范围(由计算确定，本文中处于1 000～8 000Hz之间)之内出现了明显的峰值，在有效区域外的低频区域，也出现了一个峰值，该值是由于模型本身的弯曲振动模态而非反射波引起[3]。在模态分析中，前几阶自振频率均在1kHz以下，因此，进行了以1kHz左右为截止频率的高通滤波，用于消除这些强烈的低频信号。

处理后的各模型频域分析如图5所示。

(a)SGS-1-A;(b)SGS-1-B;(c)SGS-2-A;(d)SGS-2-B;(e)SGS-3-A;(f)SGS-3-B;(g)SGS-4-A;(h)SGS-4-B图5　各模型频域图Fig.5 Frequency domain

根据图5可知：

1)注浆1与注浆2情况下，即注浆层声阻抗远小于管片声阻抗时(Zz/Z1<12%)，f1峰值十分明显，fd则不明显，频域图中干扰峰值极少，说明管片-注浆层界面反射波能量值占绝对优势。

2)注浆3情况下(Z2/Z1=38%)，f1与fd峰值均能在频域图中找到对应值，且较为明显，频域图中出现较多干扰峰值，说明在界面上发生了较为复杂的反射与折射。

3)注浆4情况下(Z2/Z1=63%)，fd峰值十分明显，f1则不明显，频域图中干扰峰值极少，说明注浆层-围岩界面反射波能量值占绝对优势。

4)本文选取的两种围岩，计算所得频域图形状上存在一定差别，但对应的峰值频率十分接近。

根据式(3)与式(5)，得到4个计算模型的峰值频率理论值，与有限元模拟结果共同列于表3：

表3　结果对比

注：括号内数值为理论值

由表3可知，在频域图中能够识别的峰值频率上，数值模拟结果与理论值吻合较好。

4结论

1)随着注浆层与管片层声阻抗比值增大，注浆层声阻抗越来越接近管片层，围岩-注浆层界面厚度频率越发地不明显。界面冲击波的反射从管片-注浆层界面占绝对优势转变为注浆层-围岩界面占绝对优势。

2)研究结果表明，注浆层声阻抗的大小对回波特性影响极大，其与管片声阻抗的相对值决定了所能探测到的界面，以及频域图上峰值频率的显著性。

3)对于界面上存在复杂反射与折射的情况下读取频域图中的峰值频率，需要对回波信号进行更多处理，由此需作进一步的理论与试验研究。

参考文献：

[1]SansaloneM,CarinoNJ,Detectingdelaminationsinconcreteslabswithandwithoutoverlaysusingtheimpact-echomethod[J]ACIMaterialsJournal86 (2) (1989) 175-184.

[2]Chung-YueWang,Chin-LungChiu,Kun-YiTsai,etal.Inspectingthecurrentthicknessofarefractorywallinsideanoperationalblastfurnaceusingtheimpactechomethod[J].NDT&EInternational, 2014(66): 43-51.

[3]MedinaR,GarridoM.Improvingimpact-echomethodbyusingcross-spectraldensity[J].JournalofSoundandVibration, 2007(304):769-778.

[4] 王智丰，周先雁，晏班夫，等. 冲击回波法检测预应力束孔管道压浆质量[J].振动与冲击, 2009, 28(1): 166-169.

WANGZhifeng,YANBanfu,ZHOUXianyan,etal.Groutingqualitytestinginprestresseddustswithinpact-echomethod[J].JournalofVibrationandShock, 2009, 28(1): 166-169.

[5] 季亚平. 考虑施工过程的盾构隧道地层位移与土压力研究[D]. 南京：河海大学, 2004.

JIYaping.Studyofstratumdisplacementandearthpressureconsideringconstructionprogramofshieldtunnel[D].Nanjing:HohaiUniversity, 2004.

[6] 刘洋希. 基于冲击回波法的预应力管道压浆质量检测[D].长沙：湖南大学, 2013.

LIUyangxi.Detectinggroutingqualityoftendonductsusingtheimpact-echomethod[D].Changsha:HunanUniversity, 2013.

[7]LinY,SansaloneM,CarinoN.J.Finiteelementstudiesoftheimpact-echoresponseofplatescontainingthinlayersandvoids[J].JournalofNondestructiveEvaluation, 1990, 9(1): 27-47.

[8] 李峥然. 盾构开挖对地层变形及邻近桩基影响研究[D].大连：大连交通大学, 2012.

LIZhengran.Researchontheproblemoftunnelingpassingacrosstheadjacentpile-foundationinshield[D].Dalian:DalianJiaotongUniversity, 2012.

Investigating the effect of acoustic impedance of the grouting rock in the shield tunnel Using impact-echo method

SU Jianhong，YAO Fei

(CollegeofCivilandTransportationEngineering，HohaiUniversity，Nanjing210098，China)

Abstract:Based on the segment-grouting-surrounding rock models in the shield tunnel and the principle that the materials’ acoustic impedance ratio has a great impact on the impact-echo test results, the segment-grouting-surrounding (SGS) rock models with different material parameters were established using finite element software MSC.MARC. The software was used to simulate the transient process of impact. The effects of different acoustic impedance values on SGS models were studied. The results show that the acoustic impedance of grouting layer has a great effect on the impact-echo characteristics. The acoustic impedance ratio of segment and grouting determines the interface that could be detected, as well as the significance of peak frequency on frequency domain.

Key words：acoustic impedance; SGS model; impact-echo method; numerical simulation

收稿日期：2015-10-11

基金项目：中央高校基本科研业务专项资助项目(2015B21414)

通讯作者：姚菲(1983-)，女，湖南凤凰人，讲师，博士，从事结构隔震与结构检测研究；E-mail:yaofei215@sina.com

中图分类号：U455.43

文献标志码：A

文章编号：1672-7029(2016)05-0938-05