基于GM(1,1)幂模型的冻胀区高速铁路轨面不平顺发展预测

郭毅，高建敏

(西南交通大学 牵引动力国家重点实验室,四川 成都 610031)

基于GM(1,1)幂模型的冻胀区高速铁路轨面不平顺发展预测

郭毅，高建敏

(西南交通大学 牵引动力国家重点实验室,四川 成都 610031)

摘要:根据冻胀区高速铁路轨面不平顺的发展特征，应用灰色系统理论，建立以冻胀区高速铁路轨面不平顺检测数据为时间序列的非等时距GM(1,1)幂模型，优化模型的初始值和背景值以提高预测精度；利用粒子群智能算法求解幂指数，并采用谐波变换生成的周期性函数与正弦函数相结合的方法对残差进行组合修正，以更好地拟合不平顺发展中的随机性成分。在此基础上，应用所建立的模型对某冻胀区高速铁路轨面不平顺在路基冻胀发育过程中的发展进行拟合预测。研究结果表明：所建立的模型能够较好地反应冻胀区高速铁路轨面不平顺在路基冻胀发生期间随时间的随机变化过程，模型能够利用40 d左右的不平顺数据较为准确的预测未来10～20 d不平顺变化情况，拟合值的平均相对误差为约5.64%，预测值的平均相对误差为约6.47%。研究结果可为冻胀区高速铁路轨面不平顺的养护维修提供参考。

关键词：高速铁路；轨面不平顺；路基冻胀；GM(1,1)幂模型；发展预测

我国季节性冻土区约占国土面积的55%，已建、在建和拟建的高速铁路与快速客运专线三分之一以上均位于深季节冻土地区[1-2]。寒区高速铁路路基冻胀是困扰高速铁路建设和运营的关键技术难题之一。路基冻胀具有普遍性、不确定性和难以避免等特点，将严重破坏轨面的整体平顺状态[3]。轨面几何不平顺作为轮轨系统的激扰源，是引起机车车辆产生振动和轮轨动作用力的主要原因[4]，当高速车辆通过冻胀区域时，由于路基冻胀变形引起的轨面几何状态的变化一方面将造成较大的轮轨附加动荷载，导致车辆运行品质下降，对行车安全性和舒适性产生威胁；另一方面，由于轨下基础的冻胀变形，造成钢轨和轨下基础受力状态变化，进而导致钢轨和轨下基础变形和伤损加剧，反过来又会恶化轨面几何状态，加剧轮轨相互作用，如此形成恶性循环，严重影响高速铁路线路的服役状态与使用寿命。针对季节性冻土地区的路基冻胀问题，目前己经釆取了多种防冻胀措施，但在实际运营中依然存在一定的冻胀变形，破坏了轨面的平顺状态，影响高速行车的动力性能。根据哈大高速铁路2012年全线冻胀观测数据，全线冻胀变形量大于零的测点数占总测点数的75.7%，冻胀量大于5 mm的测点数占总测点数的19.5%[3]。吉珲客运专线在2013-2014年监测到的数据显示，路基冻胀量大于零的测点占总监测点的80.12%，大于12 mm的监测点占全部监测点数的6.01%[5]。目前大量的研究工作围绕路基冻胀产生的原因、变化规律及其防治等开展，对于由于路基冻胀而引起的轨面不平顺变化规律及其动力影响的研究较少。基于上述背景，有必要结合实际情况，开展高速铁路路基冻胀引起的轨面不平顺特征及其变化规律的研究，掌握冻胀区高速铁路轨面几何不平顺的特点及其发展变化规律，进而建立合理的线路状态预测模型，分析与预测冻胀区高速铁路轨面几何状态变化的未来趋势与形态，以期为冻胀区高速铁路轨道养护维修计划的制订提供参考。在基于实测数据预测模型研究方面，邓聚龙在1982年创立的灰色系统理论，以部分信息已知、部分信息未知的小样本、贫信息不确定性系统为研究对象，通过对部分已知信息的生成、开发，提取有价值点的信息，实现对系统运行行为、演化规律的正确描述和有效监控[6]。目前在铁路行业，灰色系统理论已经用于轨道质量预测、路基沉降变形预测等领域，曲建军等[7-8]基于灰色GM(1,1)模型，建立了非等时距的修正模型和轨道几何状态中长期时变参数预测模型，进行了轨道质量的预测；张玉芝等[9]利用灰色GM(1,1)模型建立了动态灰色新陈代谢预测模型群，并将其用于高速铁路路基沉降变形的实时预测；郭然等[10]利用灰色GM(1,1)模型建立了具有更新机制的铁路轨道不平顺灰色预测模型，用于轨道不平顺的劣化预测。然而，GM(1,1)模型在形式上是线性模型[11]，冻胀区轨面几何不平顺受诸多因素的影响，具有较强的非线性特征。GM(1,1)幂模型的灰色作用量中的幂指数能够较好地反映原始数据的非线性特征，可用于描述和预测事物非线性发展态势[12-13]。基于此，本文结合某季节性冻土区高速铁路轨面不平顺实测数据，针对其在路基冻胀初始波动、快速发展以及冻胀稳定3个阶段的发展规律进行研究，建立了用于冻胀区高速铁路轨面几何不平顺发展预测的GM(1,1)幂模型，求解了模型的幂指数、优化了初始值和背景值并进行了残差修正，最后，结合实测数据资料，进行了预测模型的验证和分析。

1高速铁路冻胀区轨面不平顺发展特征

路基冻胀将引起轨下基础的变形和破坏，进而影响轨面几何状态的变化。通过对我国某高速铁路2012～2013年70处监测点轨面几何不平顺数据随时间变化趋势的分析表明，路基冻胀引起的轨面几何不平顺具有大致相同的变化趋势。图1所示为该线路某一典型区段路基冻胀引起的轨面不平顺幅值的发展变化情况。由图1可见，在一个冻胀周期内，高速铁路冻胀区轨面几何不平顺随时间的发展历程大致可分为冻胀初始波动、快速发展、冻胀稳定、快速回落4个阶段。该监测点在2012年11月29日至2013年1月29日这2个月内，受气温波动的影响，路基开始发生冻胀变形，由此使得轨面不平顺随之发展变化，其幅值变化范围在1.5 mm以内。而在2013年的1月29日至3月3日期间，随着气温的持续下降，路基冻深增加，冻胀变形加快发展，轨面不平顺随之快速增加，在约一个月的时间内，幅值快速增长至4.8 mm。进入3月份初期，气温有所回升，但是路基依然冻结，在该阶段，持续时间较短，轨面不平顺在0.2 mm的范围内波动。随着气温的持续升高，冻结的路基开始融化，轨面不平顺幅值随之快速回落，仅用13 d的时间，就随时间近似呈线性关系由4.98 mm回落至1.12 mm。

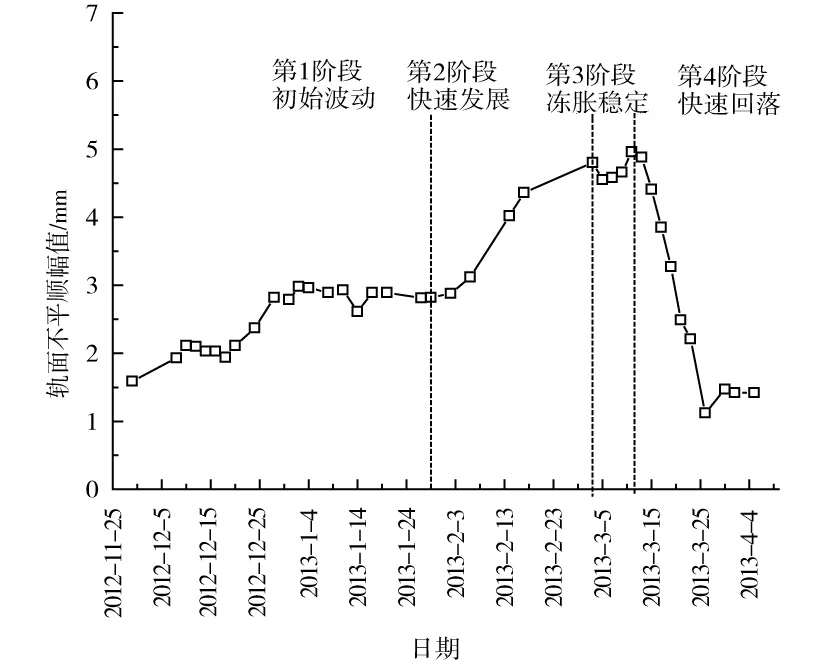
图1　路基冻胀引起的轨面不平顺发展特征Fig.1 Development characteristics of track irregularity caused by subgrade frost heaving

为了全面描述该线路由路基冻胀引起的轨面不平顺随时间的发展情况，图2给出了该高速线路70处监测点在4个阶段轨面不平顺变化率的统计情况。由图2(a)可以看出，在冻胀初始波动阶段，高速铁路路基刚开始冻结，轨面不平顺幅值波动较小，不平顺发展率主要集中在-0.02～0.025 mm/d。随着气温的持续下降，路基的冻胀变形进入快速增长阶段，导致轨面不平顺随时间快速增加，其发展变化率集中在0.05～0.2 mm/d(见图2(b))，较第一阶段明显增大。在冻胀稳定阶段，路基表层的冻胀变形基本稳定，轨面不平顺幅值在较小的区间内波动，其不平顺的发展变化率集中在-0.025～0.04 mm/d(图2(c))，不平顺发展变化率与第一阶段类似。随着气温的逐渐升高，路基出现融沉，轨面不平顺与时间近似呈线性关系急剧回落，变化率约为-0.4～-0.1 mm/d，如图2(d)所示。

(a)冻胀初始波动阶段;(b)冻胀快速发展阶段;(c)冻胀稳定发展阶段;(d)快速回落阶段图2　冻胀区轨道不平顺变化率分布图Fig.2 Variation rate distribution of track irregularity in frozen ground region

由此可见，与常规线路不平顺的发展恶化趋势相比，由路基冻胀引起的轨面几何不平顺具有发展速率快，发育、消亡周期短等特点，其发展变化具有明显的非线性、随机性特征。高速铁路冻胀区轨面不平顺的形成和发展受路基土质情况及其含水量、大气温度、荷载、轨道结构等诸多因素的共同作用[1]，无法确定和量化各因素对轨面几何不平顺发展的随机作用。而灰色系统理论恰好针对此类部分信息已知、部分信息未知的不确定性系统，仅利用系统行为数据序列建立预测模型，深入挖掘数据的发展规律，实现对系统运行行为演化规律的正确描述，进而实现对其未来变化的定量预测。因此，作者采用灰色系统理论，建立预测模型，进行冻胀区高速铁路轨面几何不平顺发展预测研究。

2灰色GM(1,1)幂模型的建立与求解

所采用的灰色GM(1,1)幂模型[6]对数据进行了前处理以提高数列的光滑度，利用单位时段差系数修正法将非等时距数列变化为等时距数列，然后利用粒子群智能算法求解了幂指数并优化了初始值和背景值，并对残差进行了组合修正，具体步骤如下。

2.1灰色GM(1,1)幂模型

2.1.1数据前处理

设冻胀区高速铁路轨面不平顺的检测数据为

Y(0)={y(0)(t1)、y(0)(t2),...,y(0)(tn)}

(1)

式中，y(0)(ti)非负。

(2)

然后进行函数cotx变化得到非等时间数据序列

X(0)={x(0)(t1)、x(0)(t2),...,x(0)(tn)}

(3)式中，x(0)(ti)=cot(y(0)′(ti)),i=1,2,...,n。

2.1.2等时间间隔处理

传统的GM(1,1)幂模型是以等时间间隔数据序列为基础，但是在实际的工程中，由于轨检车的数据采集时间不固定，所采集的轨面不平顺数据是非等时距数列，即所对应的时间序列间距Δti=ti+1-ti≠const,i=1,2,...,n。本文利用单位时段差系数修正法[15,16]对建模数据进行处理从而得到等时间间隔的数据序列

X1(0)={X1(0)(1)、X1(0)(2)，…，X1(0)(N)}

(4)

2.1.31-AGO序列生成

对经过处理的等时间间隔数据点做一次累加生成1-AGO序列

X(1)={x(1)(1)、x(1)(2),...,x(1)(n)}

(5)

2.1.4初值优化

传统的灰色建模过程中认为拟合曲线经过初始值x(0)(1)，即用建模的第1个数据作为初值，但是在实际的预测模型中，最优的拟合曲线不一定经过建模数据的某一个点。因此，本文采取给初值一个待优化的初始激扰φ，即用x1(1)=x0(1)+φ作为优化模型的初值。

2.1.5模型方程建立

对生成后的x(1)(k)建立GM(1,1)幂模型的灰色微分方程：

x(0)(k)+az(1)(k)=b(z(1)(k))γ

(6)

式中:z(1)(k)为灰导数背景值；a为发展系数，体现模型的发展态势；b为灰色作用量，反映数据变化的不确定关系。

2.1.6背景值优化

模型的拟合与预测精度取决于幂指数γ、发展系数a和灰色作用量b，而这三者的求解又与背景值z(1)(k)的构造形式有关，使得背景值成为影响模型精度的关键因素。传统模型中背景值的求解是取两点的平均值。但是，这种近似降低了GM(1,1)幂模型的精度，为了提高灰色模型精度，本文以

z(1)(k+1)=ψ*x(1)(k+1)+

(1-ψ)*x(1)(k),ψ⊂(0,1)

(7)

为背景值建立新的模型，其中ψ为背景值待优化系数。

2.1.7时间响应序列求解

对灰色微分方程做最小二乘估计可得参数列

(8)

其中

(9)

将式(8)展开可得到γ与a，b的关系式[13]：

a=

(10)

b=

(11)

式(6)的时间响应式

(12)

还原为非等间距数列中与时间t有关的函数

(13)

故可得到各时点的模拟、预测值：

(14)

式中：Δt0为平均时间间隔。

将得到的各时点的模拟、预测值还原到标准化数据：

(15)

最后，将标准化值还原至非标准化值，即为轨面不平顺的实际拟合、预测值

(16)

2.2基于粒子群算法的GM(1,1)幂模型参数

优化

粒子群算法是一种基于群体的随机优化技术，具有群体智能、迭代格式简单、可快速收敛到最优解所在区域等优点[17]。根据2.1节所建立的模型，可知共有3个待求解模型参数，即幂指数γ、初值优化激扰φ以及背景值优化系数ψ。为了利用粒子群优化算法求解GM(1,1)幂模型中的模型参数，定义该模型的平均相对误差函数为：

(17)

这样GM(1，1)幂模型中参数优化问题可变为利用粒子群算法求解minf(γ,φ,ψ)。

2.3残差序列的修正

利用上述灰色GM(1,1)幂模型可对轨面不平顺的发展趋势进行拟合预测，但拟合出的趋势曲线通常是光滑的，不具有波动特征。而其残差序列通常在零值附近波动，具有不太规律的周期性，说明原始数据隐含有一定的周期性成分和随机成分。采用谐波变换生成的周期性函数能反映出随机波动中的大部分周期性成分，正弦函数则反映出随机波动中残留的小部分随机波形成分[7]。本文为提高模型的预测精度，采用谐波变换生成的周期性函数与正弦函数相结合[8]对残差进行组合修正。

设残差序列为：

(18)

利用谐波变换生成的周期序列函数对E(ti)进行拟合

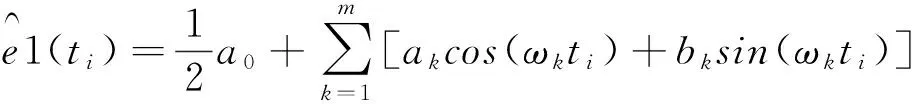
i=1,2...,n

(19)

利用残差序列波形平均特征构造正弦残差修正周期函数，其模型为

(20)

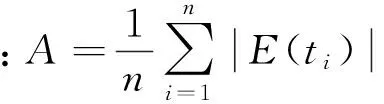
引入权重系数α和β对式(19)和(20)进行权重组合得到残差的组合修正模型为

(21)

式中: α+β=1，α和β的取值以同样模型数据的平均相对误差最小为原则确定。

最终得到的GM(1，1)幂修正模型为：

(22)

2.4模型的后验差检验

为检验所建立模型的准确性和可靠性，用后验差检验方法[18]对其进行精度检验和预测值精度估计。一般，根据小误差概率P和均方差比值C的大小，将预测精度分为4类，如表1所示。

表1　精度检验等级参照表

3算例分析

应用2012年11月至2013年1月某高速铁路K147.548 km处轨面不平顺实际检测数据，进行了基于GM(1,1)幂模型的高速铁路冻胀区轨面不平顺发展预测分析，借此验证了模型的可行性与可靠性。所选用的轨面不平顺原始数据如表2所示。

取前15组数据样本建立模型，将原始数据经过标准化(开4次方)处理，按照上述步骤求解得到幂指数γ=1.332 1，背景值优化系数ψ=0.469 5，初值优化激扰φ=-0.002 8。最后计算得到的拟合结果如图3和表3所示。

图3　轨面不平顺实测值与拟合值曲线对比Fig.3 Curve comparison between tested values and fitted values of track irregularity

由图3和表3可以看出，所建立的GM(1,1)幂模型能够模拟冻胀区轨面不平顺随时间的变化情况，拟合精度较高。预测模型的后验差检验结果为：均方差比值C=0.074 1，小误差概率P=1，精度等级为一级，拟合值的平均相对误差为1.46%，拟合值平均绝对误差为0.028。由此说明，该模型拟合精度较高，能够用于外推预测。

利用所建立的预测模型对上述所选取路段2013年1月14至2013年1月29日所检测的5组数据进行了预测，并与实测数据进行了对比，其结果如表4所示。由表4结果可见，预测值的平均相对误差为4.56%，平均绝对误差为0.212，模型的预测值与实测值较为接近，预测精度较高。

表2　高速铁路冻胀区轨面不平顺实测值

表3轨面不平顺实测值与拟合值的数值比较

Table 3 Numerical comparison between tested values and fitted values of track irregularity

序号相对时间实测数据拟合数据残差相对误差102.112.0970.0130.62%292.372.3580.0120.51%3111.891.897-0.0070.37%4131.841.7960.0442.39%5151.641.640006171.751.7260.0241.37%7191.641.678-0.0382.32%8211.361.385-0.0251.84%9251.221.226-0.0060.49%10291.921.8420.0784.06%11321.911.8300.0804.19%12341.962.000-0.0402.04%13362.172.174-0.0040.18%14402.862.875-0.0150.52%15433.073.0380.0321.04%

表4轨面不平顺实测值与预测值的比较

Table 4 Comparison between tested values and predictive values of track irregularity

序号相对时间实测数据拟合数据残差相对误差16463.443.454-0.0140.41%17494.13.8000.3007.32%18524.484.1780.3026.74%19595.314.9550.3556.69%20615.415.3210.0891.65%

此外，将该高速线路70余处冻胀监测点的不平顺数据按时间序列生成128组有效数据样本，利用所建立的GM(1,1)幂模型对这些样本数据进行了拟合和预测。图4所示为这128组样本数据的拟合和预测值平均相对误差的统计情况。由图4结果可以看出，拟合值的平均相对误差集中在1%～8%之间，平均值约为5.64%；预测值的平均相对误差集中在2%～8%之间，平均值约为6.47%。由此进一步说明，本文所建立的模型具有较高的拟合与预测精度，可以用于冻胀区高速铁路轨面不平顺发展预测之用。

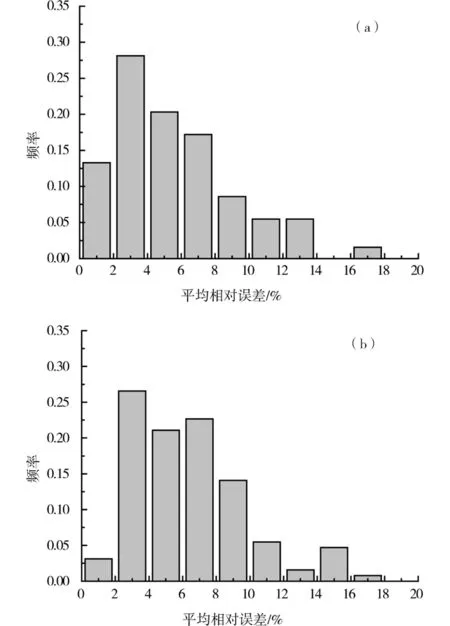
(a)拟合值平均相对误差;(b)预测值平均相对误差图4　拟合和预测值平均相对误差分布图Fig.4 Mean relative error distribution of fitted values and predictive values

上述计算和分析结果表明，所建立的GM(1,1)幂模型能够利用高速铁路冻胀区40 d左右的不平顺数据较为准确地预测未来10～20 d的不平顺变化情况，如此可为高速铁路冻胀区轨道的养护维修提供一定的缓冲时间，有助于工务部门合理的制订和实施养护维修计划。

4结论

1)冻胀区高速铁路路基冻胀引起的轨面几何不平顺与常规线路轨面几何不平顺相比具有发展速率快，发育、消亡周期短等特点，其发展变化具有明显的非线性、随机性特征。

2)采用基于粒子群算法的GM(1,1)幂模型，能够模拟和预测路基冻胀从发生到稳定这一过程中，轨面不平顺在诸多影响因素共同作用下随时间的发展恶化过程。

3)模型中的幂指数能够较好的模拟轨面不平顺在路基冻胀过程中的非线性发展态势。

4)本模型为解决冻胀区高速铁路轨面不平顺发展因素的不确定性因果关系和对轨面不平顺发展进行中短期预测提供了一种方法。在保障高速铁路的安全运营、实现预防性计划维修等方面能够为工务部门提供参考。

参考文献：

[1] 杜晓燕, 叶阳升, 张千里, 等. 季节性冻土区高速铁路路基冻深研究[J]. 中国铁道科学, 2015, 36(2): 11-17.

DU Xiaoyan, YE Yangsheng, ZHANG Qianli, et al. Freezing depth of high speed railway subgrade in seasonally frozen ground region[J]. China Railway Science, 2015, 36(2): 11-17.

[2] 王天亮. 寒区路基改良土力学特性分析[M]. 北京: 中国铁道出版社, 2014.

WANG Tianliang. Mechanical properties analyses of the roadbed improved soil in cold regions[M]. Beijing: Chinese Railway Press, 2014.

[3] 张先军. 哈大高速铁路路基冻胀规律及影响因素分析[J]. 铁道标准设计, 2013, (7): 8-12.

ZHANG Xianjun. Analysis of frost heave laws in subgrade on Haerbin-Dalian high-speed railway and its influence factors[J]. Railway Standard Design, 2013, (7): 8-12.

[4] 罗林. 轮轨系统轨道平顺状态的控制[M]. 北京:中国铁道出版社, 2006.

LUO Lin. Control of track irregularity state of wheel / rail system[M]. Beijing: Chinese Railway Press, 2006.

[5] 黄新文, 崔俊杰, 易菊香. 吉珲客运专线路基冻胀变形及影响因素分析[J]. 铁道标准设计, 2015, 59(8): 39-42.

HUANG Xinwen, CUI Junjie, YI Juxiang. Analysis of frost heave deformation of the subgrade on Jilin-Hunchun dedicated passenger railway line[J]. Railway Standard Design, 2015, 59(8): 39-42.

[6] 党耀国. 灰色预测与决策模型研究[M]. 北京: 科学出版社, 2009.

DANG Yaoguo. Research on grey prediction and decision-making model[M]. Beijing: Science Press, 2009.

[7] 曲建军, 高亮, 张新奎, 等. 基于灰色GM(1,1)非等时距修正模型的轨道质量预测[J]. 中国铁道科学, 2009, 30(3): 5-8.

QU Jianjun, GAO Liang, ZHANG Xinkui, et al. A prediction method for track quality based on grey GM(1,1) non-equal time interval correction model[J]. China Railway Science, 2009, 30(3): 5-8.

[8] 曲建军, 高亮, 田新宇, 等. 基于灰色理论的轨道几何状态中长期时变参数预测模型的研究[J]. 铁道学报, 2010, 32(2): 55-59.

QU Jianjun, GAO Liang, TIAN Xinyu， et al. Study on the mid&long term prediction model of track geometry state based on the grey time-varying parameters theory[J]. Journal of the China Railway Society, 2010, 32(2): 55-59.

[9] 张玉芝, 杜彦良, 孙宝臣. 改进的动态灰色模型在高铁路基变形预测中的应用[J]. 铁道科学与工程学报, 2013, 10(2): 56-61.

ZHANG Yuzhi, DU Yanliang, SUN Baochen. Application of improved dynamic grey model in high-speed railway bed settlement prediction[J]. Journal of Railway Science and Engineering, 2013, 10(2): 56-61.

[10] 郭然, 韩宝明, 李得伟, 等. 具有更新机制的铁路轨道不平顺灰色预测模型[J]. 中南大学学报(自然科学版), 2013, 44(10): 4334-4341.

GUO Ran, HAN Baoming, LI Dewei, et al. Grey prediction model for track irregularity with update mechanism[J]. Journal of Central South University(Science and Technology), 2013, 44(10): 4334-4341.

[11] 王正新, 党耀国, 刘思峰,等. GM(1,1)幂模型求解方法及其解的性质[J]. 系统工程与电子技术, 2009, 31(10): 2380-2383.

WANG Zhengxin, DANG Yaoguo, LIU Sifeng, et al. Solution of GM(1,1) power model and its properties[J]. Systems Engineering and Electronics, 2009, 31(10): 2380-2383.

[12] 李军亮, 肖新平, 廖锐全. 非等间隔GM(1,1)幂模型及应用[J]. 系统工程理论与实践, 2010, 30(3): 490-495.

LI Junliang, XIAO Xinping, LIAO Ruiquan. Non-equidistance GM(1,1) power and its application[J].Systems Engineering-Theory&Practice, 2010, 30(3): 490-495.

[13] 王正新, 党耀国, 刘思峰. 非等间距GM (1,1)幂模型及其工程应用[J]. 中国工程科学, 2012, 14(7): 98-102.

WANG Zhengxin, DANG Yaoguo, LIU Sifeng. Non-equidistant GM(1,1) power model and its application in engineering[J]. Engineering Sciences, 2012, 14(7): 98-102.

[14] 李翠凤, 戴文战. 基于函数cotx变换的灰色建模方法[J]. 系统工程, 2005, 23(3): 110-114.

LI Cuifeng, DAI Wenzhan. An approach of the grey modelling based on cotxtransform action[J]. Systems Engineering, 2005, 23(3): 110-114.

[15] 黄声享, 李志成. 工程建筑沉降预测的非等间距灰色建模[J]. 地理空间信息, 2004, 2(1): 41-43.

HUANG Sengxiang, LI Zhicheng. Grey modeling of non-equidistant data sequent for forecasting subsidence of the engineering buildings[J]. Geospatial Information, 2004, 2(1): 41-43.

[16] 梅红, 孙泽信. 非等间距GM(1,1)模型的改进及预测分析[J]. 河海大学学报(自然科学版), 2010, 38 (5): 569-574.

MEI Hong, SUN Zexin. Improvement and prediction of non-equal interval GM(1,1) model[J]. Journal of Hehai University(Natural Sciences), 2010, 38(5): 569-574.

[17] 高飞. Matlab智能算法超级学习手册[M]. 北京:人民邮电出版社, 2014.

GAO Fei. Super learning manual of Matlab intelligent algorithm [M]. Beijing: Posts&Telecom Press, 2014.

[18] 罗佑新. 灰色系统理论及其在机械工程中的应用[M]. 长沙: 国防科技大学出版社, 2001.

LUO Youxin. Grey system theory and its application in mechanical engineering[M]. Changsha: National University of Defense Technology Press, 2001.

Track irregularity evolution prediction for high speed railways in frozen ground region based on GM(1,1) power model

GUO Yi, GAO Jianmin

(State Key Laboratory of Traction Power, Southwest Jiaotong University, Chengdu 610031, China)

Abstract：According to the evolving characteristics of track irregularity of high speed railway in frozen ground region, the non-equal interval GM(1,1) power model was established based on the grey system theory. When establishing the GM(1,1) model, the track irregularity test data of high speed railway in frozen ground region were treated as the time series. The initial values and background values of the model were optimized to improve the prediction accuracy. The power exponent was solved by using particle swarm intelligence algorithm. In order to fit the random components of track irregularities better, periodic functions generated by harmonic transform and sine function were introduced to modify the residual error. Accordingly, the track irregularity evolution of high speed railway in frozen ground region during the process of the subgrade frost heaving was predicted. The results show that the model can well reflect the time-dependent random fluctuation characteristics of track irregularity evolution of high speed railway in frozen ground region. The average relative error of the fitted values is 5.64% and the average relative error of the predictive value is 6.47%. This model may provide references for the maintenance of track irregularity of high speed railway in frozen ground region.

Key words：high speed railway；track irregularity；subgrade frost heaving；GM(1,1) power model；development prediction

收稿日期：2015-11-12

基金项目：国家重点基础研究发展计划(973计划)项目(2013CB036205，2013CB036206)；中国铁路总公司科技研究开发计划资助项目(2014G001-1)；中央高校基本科研业务费专项资金资助项目(2682015CX045)；牵引动力国家重点实验室自主研究资助项目(2014TPL_T01)

通讯作者：高建敏(1981-)，女，河北南和人，副研究员，博士，从事铁路轨道不平顺及其管理研究；E-mail：jmgao@swjtu.edu.cn

中图分类号：U212.2

文献标志码：A

文章编号：1672-7029(2016)05-0791-09