基于改进的QPSO-WNN滚动算法的铁路沿线短期风速预测

路学海，潘迪夫，韩锟，李继松

(中南大学 交通运输工程学院，湖南 长沙 410075)

基于改进的QPSO-WNN滚动算法的铁路沿线短期风速预测

路学海，潘迪夫，韩锟，李继松

(中南大学 交通运输工程学院，湖南 长沙 410075)

摘要:为了提高传统神经网络对非平稳风速的预测精度，提出将改进的量子粒子群算法(QPSO)和小波神经网络(WNN)相结合的滚动预测算法。将小波神经网络的初始连接权值及小波基函数参数组成一个多维向量，作为改进量子粒子群算法的粒子进行计算更新，将搜索得到的解空间范围内全局最优参数作为小波神经网络的初始参数。针对已经训练好的小波神经网络的预测误差会随着时间推移而增大的问题，采用每隔1h滚动式训练的方法训练小波神经网络。运用优化算法对我国海南东环铁路某测风站实测风速进行超前多步预测。实例结果表明，相对于传统小波神经网络，优化算法的风速平均相对误差和均方根误差都有所降低，其超前3min、9min、15min的风速预测平均相对误差为8.28%、9.93%、11.37%。关键词：风速预测；量子粒子群；小波神经网络

大风是影响铁路运输安全性和稳定性的主要气象灾害之一，其引发的列车安全事故在日本、中国、比利时、瑞士等国家时有发生[1]。为了应对铁路沿线强风对列车行车安全所造成的危害，我国在兰新铁路建立了监测预警指挥系统[2]。其原理是在铁路沿线强风区域设置测风站，实时采集铁路沿线风速信息，安装风速仪和采集单元，实时采集风速、风向数据，当数据超出阈值时发出报警，铁路调度部门确认报警信息和现场情况后，及时采取应对措施，比如减速、停车或躲避等。而如果铁路调度部门能够提前掌握铁路沿线监控区域的风速短期变化趋势，调度人员就可以留出充足的决策时间来确定合理、适度的对策，这对于预防事故、保证行车安全和效率会起到更好的作用。

实现动态监控指挥的核心是铁路沿线风速的超前多步短期预测。铁路风速预测研究近年来受到西方铁路发达国家的日益重视。U.Hoppmann等[3]提出了一种通过统计沿线历史风速数据以实现外推估计的风速预测方法。M.Shimamura等[4]也提出了一种基于卡尔曼滤波递推的风速短期预测方法。潘迪夫等[5-8]也开展了铁路沿线风速预测研究，并提出了基于时间序列分析等理论、卡尔曼滤波理论以及神经网络等短期风速预测方法。神经网络由于其出色的非线性映射能力，建模简单，已逐渐成为研究非平稳信号预测的经典方法[9-11]。但神经网络模型自身存在诸多问题，如在确定网络初始权值、神经元节点数、选择网络训练样本数据格式等方面存在主观性和盲目性[12]。在此，本文选择小波神经网络为基础算法，利用时间序列建模方法确定网络结构，将改进的量子粒子群算法优化小波神经网络的初始参数。以我国沿海铁路某测风站实测风速序列为例，提出改进的QPSO-WNN滚动算法，实现对风速的超前多步预测。

1小波神经网络

小波神经网络是小波分析与人工神经网络结合的产物，按照其结构形式分为两大类[13]：松散型网络和紧致型网络。本文采用小波神经网络是以BP神经网络拓扑结构为基础，把小波基函数作为隐含层节点的传递函数，小波函数的伸缩和平移系数代替常规网络输入层到隐含层的权值和阈值。信号前向传播的同时误差反向传播神经网络。小波神经网络拓扑结构如图1所示。

图1　小波神经网络结构Fig.1 Wavelet neural network structure

图中，小波神经网络的输入层节点个数为m，隐含层节点数为n，输出层节点个数为1。小波神经网络的输出为：

(1)

式中：xj为网络的第j个输入；y为网络的输出；wij为输入节点j与隐节点i之间的权值；wi为隐节点i与输出节点之间的权值；ψi为小波基函数，ai和bi分别为第i个隐节点的伸缩因子和平移因子。

本文采用的小波基函数为Morlet小波函数[14]，数学公式为：

ψ(t)=cos(1.75t)exp(-t2/2)

(2)

小波神经网络的学习过程主要基于传统BP算法，采用梯度修正法修正网络的权值和小波基函数参数，从而使小波神经网络预测输出不断逼近期望输出。小波神经网络参数修正过程如下：

1)计算网络预测误差。

(3)

式中：N为样本总数；dp为网络的期望输出；yp为网络的实际输出。

2)根据预测误差修正小波神经网络权值和小波基函数系数。

(4)

(5)

(6)

(7)

(8)

小波神经网络算法训练步骤如下：

步骤1：网络初始化。随机初始化小波函数伸缩因子、平移因子以及网络连接权值，设置网络学习速率。

步骤2：样本分类。把样本分为训练样本和测试样本，训练样本用于训练网络，测试样本用于测试网络预测精度。

步骤3：计算预测输出。把训练样本输入网络，计算网络预测输出并且计算网络输出与期望输出的误差。

步骤4：权值及参数修正。根据误差修正网络权值和小波函数参数，使网络预测值逼近期望值。

步骤5：判断算法是否结束，如果没有结束，返回步骤3。

2改进的量子粒子群算法

量子粒子群算法(QuantumParticleSwarmOptimization，QPSO)是结合量子计算方法和粒子群算法的一种新型的粒子群算法。QPSO算法已广泛应用于函数优化、数据挖掘、模糊控制学、神经网络训练、图像处理等领域。本文主要介绍李士勇等人提出的量子粒子群算法[15]。量子粒子群算法在迭代后期会导致种群多样性下降、易陷入局部最优、收敛速度变慢和早熟收敛，为进一步提高QPSO算法的性能，在研究不同的QPSO算法参数对算法性能的影响分析的基础上，本文提出一种自适应参数调整量子粒子群算法。改进算法从变异处理、惯性权重、学习因子三个方面对QPSO算法进行改进。

1)变异处理的改进

将量子粒子群算法中变异处理的量子非门改成Hadamard门来实现粒子位置的变异Hadamard门实现的变异操作过程为：

(9)

2)惯性权重自适应调整

在应用中，对于高适应度的粒子应重点开发自身领域，寻找局部最优值，加快算法收敛，惯性权重应较小；对于低适应度的粒子应重点探索其他领域，寻找全局最优值，跳出局部最优点，避免算法早熟现象，惯性权重应较大。基于这种理念，提出一种惯性权重根据粒子当前适应度进行自适应调整的方法：

(10)

式中：wmin为设定的惯性权重最小值；fit(x)为每个粒子当前的适应度，fitw为种群最差粒子的适应度，fitb为种群最好粒子的适应度。每个粒子当前的惯性权重通过粒子当前的适应度与全局最好适应度和最差适应度进行比较进行自适应调整，使每个粒子有目标地向着全局最优解的方向和位置移动，能够提高算法全局搜索能力和优化效率。

3)学习因子自适应调整

通过分析得出对于高适应度的粒子应重点开发自身领域，加速系数应较小；对于低适应度的粒子应重点探索其他领域，加速系数应较大。同样基于寻找全局最优、提高优化效率和让每个粒子都能有目标地向最好的方向、位置和以更快的速度移动的理念，提出一种自身因子和全局因子根据当前适应度和惯性权重进行自适应调整方法：

(11)

式中：自身因子η1根据算法权重自适应调整，全局因子η2根据自身因子和当前全局最好粒子适应度和最差粒子适应度有目标地进行调整，能够提高算法全局搜索能力和优化效率。

通过QPSO算法参数对全局搜索能力和优化效率的影响分析进行QPSO算法改进：Hadamard门来实现粒子位置的变异保持了种群多样性；惯性权重、自身因子和全局因子根据粒子当前适应度进行自适应调整。改进的量子粒子群算法能够有目标地更快地找到全局最优解。

3基于改进QPSO-WNN滚动算法建模

小波神经网络结合了小波分析与人工神经网络两者的优点，其结构简单，收敛速度快，学习能力强，精度更高，而且小波神经网络的基元和整个结构是依据小波分析理论确定的，避免BP神经网络等结构设计上的盲目性。本文采用小波神经网络作为预测模型。3.1小波神经网络各层神经元数目的确定

本文所描述的单测风站单维非平稳风速信号，建立多输入单输出小波神经网络结构。对于输入层神经元个数，本文引入时间序列模型的方法来确定。

1) 利用Pandit-Wu时序建模方案的自相关与偏相关方法，识别风速序列所属的时序模型类型。

2)利用AIC或者FPE准则对所建立的时间序列模型进行定阶，确定模型的最优阶次，然后计算模型的待估参数，建立模型的预测方程。通过方程即可看出风速历史序列与当前时刻序列的关系，从而确定小波神经网络的最优输入层神经元数目。

3)隐含层神经元的个数根据经验公式来确定。

(12)

(13)

式中：m为输入层神经元数目；n为输出层神经元数目；

3.2基于改进量子粒子群算法的小波神经网络初始参数优化

小波神经网络初始参数的随意给定，导致模型预测精度的不稳定，为了寻找比较好的初始值，本文提出用改进的量子粒子群算法优化小波神经网络的初始参数，包括网络的初始权值以及小波基函数的平移因子和伸缩因子，寻找全局最优初始参数，具体步骤如下:

步骤1：粒子编码及初始化。对于有m个输入，隐含层神经元个数为n的小波神经网络，其需要优化的参数包括m*n个输入层到隐含层的权值、n个隐含层到输出层的权值、n个小波基函数平移因子和n个小波基函数伸缩因子。根据量子位的概率幅随机产生n个粒子，并设置参数初值和变异概率。

步骤2：解空间变换。

(14)

式中：Yi(t)和di(t)分别代表着网络实际输出值和样本值。

步骤4：算法参数更新。根据适应度值求出个体最优值、全局最优值和全局最差值，并根据式(10)和式(11)更新算法的惯性权重和学习因子的值。

步骤5：粒子状态更新及变异处理。对粒子状态进行更新。根据式(9)进行变异处理。

步骤6：判断算法是否结束，结束则输出结果，没有结束则返回步骤2。

3.3小波神经网络滚动算法

已经训练好的小波神经网络的预测误差会随着时间的推移而增大，这是因为训练好的神经网络的权值和小波基函数的参数不再随时间改变从而造成权值和阈值不适应若干时刻后的风速预测。为此本文提出小波神经网络滚动算法，即采用滚动的方式来训练小波神经网络。滚动训练的思想是将归一化的风速样本数据来训练小波神经网络，用来预测接下来1h时间内的风速；然后将原来的风速样本数据加上这1h的风速数据组成新的样本数据再训练小波神经网络参数，使得网络参数适用最新的风速变化特性，预测下1h时间的风速；按照这样滚动方式每训练一次网络就预测1h时间的风速，直至预测完成。 为了提高网络训练速度，将前一次训练好的小波神经网络的作为当前训练神经网络权值和阈值的初值。具体步骤如图2所示：

图2　小波神经网络滚动算法建模步骤Fig.2 Wavelet neural network scroll algorithm modeling steps

4算例分析

运用本文提出的优化算法对我国海南东环铁路某测风站实测原始风速序列ν(t)(每3min一个采样点)进行建模和预测。原始风速序列3min平均化处理后如图3所示。取前300个数进行建模分析，后100个数据检验模型。

图3　V(t)原始风速序列Fig.3 V(t) original Winds sequence

4.1模型结构确定及算法实现

1)对风速序列差分至平稳后，通过观察序列样本的自相关系数(ACF)和偏自相关系数(PACF)，序列ν(t)满足高阶自回归或自回归滑动平均模型。鉴于本文对风速实时要求，为了降低后续参数估计计算量，选择对序列ν(t)建立高阶自回归模型。利用FPE准则确定上面步骤所定自回归模型的最优阶次。然后运用矩估计法计算模型待估参数。序列ν(t)最优拟合模型为AR(5)，参数估计计算后获得的模型预测差分方程为：

Xt=-0.096 2Xt-1+0.026 3Xt-2-0.169 9Xt-3-0.134 0Xt-4-0.207 7Xt-5-1.581 6Xt-6+at

(15)

式中：at为模型残差。

方程揭示了该段风速中历史序列与当前时刻序列的关系。因此可确定网络输入层神经元数目为6，输出层神经元节点数为1个。将输入层和输出层神经元数目代入到经验公式确定隐含层神经元个数为10个。

2)用改进的量子粒子群算法优化小波神经网络的初始连接权值以及小波基函数参数。设定种群规模为50，迭代次数为50代。将序列ν(t)前300个数据分成294组训练样本，每步迭代计算的样本均方误差和种群总适应度如图4和5所示。

2个曲线变化规律直接验证了采用改进的量子粒子群算法优化小波神经网络初始连接权值和小波基函数参数是可行的,相对于神经网络算法原来的随机分配初始权值,量子粒子群算法的优化性能显而易见。

图4　改进QPSO算法标准误差变化曲线Fig.4 Standard deviation curve of improved QPSO algorithm

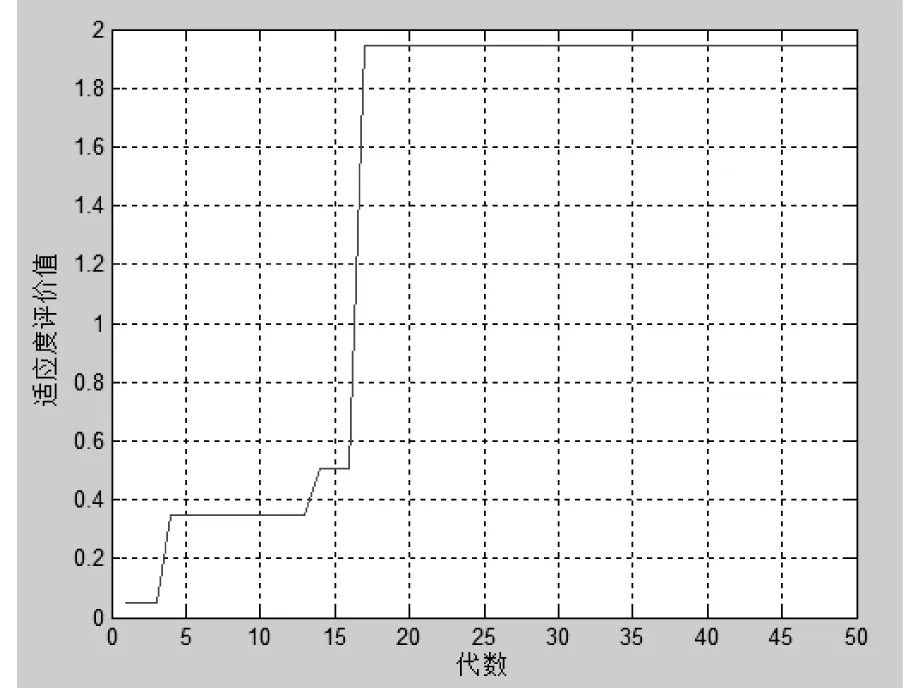
图5　改进QPSO算法适应度值变化曲线Fig.5 Fitness value curve of improved QPSO algorithm

将以上改进的量子粒子群算法搜索到的最优参数作为小波神经网络的初始连接权值和小波基函数的初始参数。把ν(t)序列前300个风速数据样本的数据格式分为294组神经网络训练样本,网络输入层节点数为6，隐含层节点数为10，输出层节点数为1，迭代次数为500次，学习速率为0.01，进行归一化处计算后对小波神经网络进行训练。训练完成后用后100个数据进行模型验证。

4.2预测结果分析

1)风速预测仿真与分析

本文基于WNN模型、改进QPSO-WNN模型、改进QPSO-WNN滚动模型分别对风速序列ν(t)进行预测。得到超前1步，3步和5步预测结果如图6，7和8所示。

图6　序列ν(t)超前1步预测结果Fig.6 Sequenceν(t) 1-step ahead prediction

图7　序列ν(t)超前3步预测结果Fig.7 Sequenceν(t) 3-step ahead prediction

图8　序列ν(t)超前5步预测结果Fig.8 Sequenceν(t) 5-step ahead prediction

由图9～11 可知：随着模型超前预测步数的增大，改进的QPSO-WNN算法相比传统的WNN算法在风速预测精度上有了较为明显的提高，而改进的QPSO-WNN滚动算法相比不滚动算法在预测精度上也有一定的提升。

2)预测模型评价标准

评价预测结果时，本文采用传统的统计学指标平均绝对百分误差(MAPE)和均方根误差(RMSE)来分析预测结果，计算公式如下：

(16)

(17)

3种模型超前1步，3步和5步预测精度评价结果如表1-3所示。

表1　超前1步预测结果分析表

表2　超前3步预测结果分析表

表3　超前5步预测结果分析表

由表1～3可知：改进的QPSO-WNN算法相对传统WNN算法超前1步，3步和5步预测的平均相对误差和均方根误差都有了明显的降低，而改进QPSO-WNN滚动算法的预测精度也有一定的提高，其超前1步，3步和5步的风速预测平均相对误差为8.28%，9.93%和11.37%。

5结论

1)本文提出将改进的量子粒子群算法和小波神经网络相结合的滚动预测算法用于铁路沿线风速预测。利用时间序列建模方法确定网络输入层的神经元节点数，从而克服了神经网络参数确定难度大的缺点。利用改进的量子粒子群算法在解空间范围内搜索小波神经网络最优初值参数，实现了小波神经网络参数全局最优化。同时本文采用每隔1h滚动式训练的方法训练小波神经网络，有效解决了小波神经网络的预测误差随着时间推移而增大的问题。

2)将本文提出的改进QPSO-WNN滚动算法应用于铁路沿线风速预测中，仿真实验结果表明相比传统的WNN算法，本方法具有更高的预测精度，预测的平均相对误差以及均方根误差都有明显的降低，其超前1步、3步和5步的平均相对误差为8.28%，9.93%和11.37%，具有一定的工程应用价值。

参考文献：

[1]ChristopherJBaker，MarkSterling.Aerodynamicforcesonmultipleunittrainsincrosswinds[J].JournalofFluidsEngineering，2009(131):101-103.

[2] 薛洁.新疆铁路大风监测系统[J].新疆气象，2002，25(5) :32-34.

XUEJie.RailwaygalemonitoringsysteminXinjiang[J].BimonthlyofXinjiangMeteorology，2002，25(5):32-34.

[3]HppmannU，KoenigS，TielkesT，etal.Ashort-termstrongwindpredictionmodelforrailwayapplication:designandverification[J]．JournalofWindEngineeringandIndustrialAerodynamics，2002，90(10): 1127-1134．

[4]ShimamuraM．Studyonstrongwindpredictingtechniqueforsafetymanagementoftrainoperation[J]．JapaneseRailwayEngineering，1995，134 (9): 15-18．

[5] 潘迪夫，刘辉，李燕飞，等.青藏铁路格拉段沿线风速短时预测方法[J]. 中国铁道科学，2009， 29(5): 129-133.

PANDifu，LIUHui，LIYanfei,etal.Ashort-termforecastmethodforwindspeedalongGolmud-LhasasectionofQinghai-Tibetrailway[J].ChinaRailwayScience，2009，29(5): 129-133.

[6] 刘辉，潘迪夫，李燕飞.基于列车运行安全的青藏铁路大风预测优化模型与算法[J]. 武汉理工大学学报: 交通科学与工程版，2008， 32(6): 986-989.

LIUHui，PANDifu，LIYanfei.Qinghai-Tibetrailwaygaleforecastingoptimizationmodelandalgorithmbasedontrainrunningsafety[J].JournalofWuhanUniversityofTechnology(TransportationScience&Engineering) ，2008， 32(6): 986-989.

[7] 刘辉，田红旗，ChenChao,等.基于小波分析法与神经网络法的非平稳风速信号短期预测优化算法[J].中南大学学报：自然科学版，2011，42(9)：2704-2711.

LIUHui，TIANHongqi，CHENChao，etal.Short-termforecastingoptimizationalgorithmforunsteadywindspeedsignalbasedonwaveletanalysismethodandneutralnetworksmethod[J].JournalofCentralSouthUniversity(ScienceandTechnology), 2011，42(9)：2704-2711.

[8]LiuHui，TianHongqi，LiYanfei.Short-termforecastingoptimizationalgorithmsforwindspeedalongQinghai-Tibetrailwaybasedondifferentintelligentmodelingtheories[J].JournalofCentralSouthUniversityofTechnology(EnglishEdition). 2009,16(4):690-696.

[9] 胡卫东，曹文贵.基于粒子群BP网络混合算法的边坡稳定性评价[J].铁道科学与工程学报，2015，12(1)：66-71.

HUWeidong，CAOWengui.SlopestabilityevaluationbasedonhybridalgorithmofparticleswarmoptimizationandBPneuralnetwork[J].JournalofRailwayScienceEngineering，2015，12(1)：66-71.

[10] 吴华稳，甄津，王宇，等.基于径向基神经网络铁路货运量预测研究[J].铁道科学与工程学报，2014，11(4)：109-114.

WUHuawen，ZHENJin，WANGYu，etal.RailwaypassengerandfreightpredictionbasedonRBFneuralnetworktheory[J].JournalofRailwayScienceEngineering，2014，11(4)：109-114.

[11] 吴伟，符卓，王晓.运输通道客运量预测方法[J].铁道科学与工程学报，2012，9(5)：96-102.

WUWei，FUZhuo，WANGXiao.Passengervolumeforecastmethodfortransportcorridor[J].JournalofRailwayScienceEngineering，2012，9(5)：96-102.

[12]MohammadM，HasanR，HosseinK.Anewstrategyforwindspeedforecastingusingartificialintelligentmethods[J].RenewableEnergy，2009，34(3): 845-848.

[13] 杨超，王志伟. 经GA优化的WNN在交通流预测中的应用[J]. 计算机工程，2011，37(14): 149-151.

YANGChao，WANGZhiwei.Applicationofwaveletneuralnetworkoptimizedbygeneticalgorithmintrafficvolumeprediction[J].ComputerEngineering，2011，37(14): 149-151.

[14] 李国良，李忠福，谢洪涛，等.基于IGA-BP算法的小波神经网络模型及应用[J].系统工程，2012，30(10):112-117.

LIGuoliang,LIZhongfu，XIEHongtao,etal.ModelandapplicationofwaveletneuralnetworkbasedonIGA-BP[J].SystemsEngineering，2012，30(10):112-117.

[15] 李士勇，李盼池.求解连续空间优化问题的量子粒子群算法[J].量子电子学报，2007，24(5)：569-574.

LIShiyong，LIPanchi.Quantumparticleswarmsalgorithmforcontinuousspaceoptimization[J].ChineseJournalofQuantumElectronics，2007，24(5)：569-574.

Railway short-term wind speed prediction based onimproved QPSO-WNN rolling algorithm

LU Xuehai, PAN Difu, HAN Kun, LI Jisong

(SchoolofTrafficandTransportationEngineering,CentralSouthUniversity,Changsha410075,China)

Abstract:This paper combined Improved Quantum Particle Swarm Optimization(QPSO) with Wavelet Neural Network (WNN) to improve the prediction accuracy of Traditional Neural Networks for non-steady wind. A multi-dimensional vector consisting of WNN initial connection weights and wavelet function parameters served as variables of Improved Quantum Particle Swarm Algorithm to update calculation. The global optimal parameters were obtained and used in initial parameters of Wavelet Neural Network. A problem that the forecast error of trained Wavelet Neural Network would increase by time was solved using rolling training method to Wavelet Neural Network every one hour. This optimized algorithm was tested in one of the wind stations in Hainan East Central Railway to multi-step forecast wind speed. The results show that average relative error and root mean square error of average wind speed are reduced. Ahead of 3min, 9min, 15min of the wind speed, the relative error of average wind speed is 8.28%, 9.93%, 11.37% respectively.

Key words:wind speed prediction; quantum particle swarm optimization; wavelet neural network

收稿日期：2015-11-02

基金项目：国家自然科学基金资助项目(U1334205)

通讯作者：潘迪夫(1957-)，男，广东兴宁人，教授，从事机车车辆控制与智能测控技术的研究；E-mail:difipan@csu.edu.cn

中图分类号：U298.12

文献标志码：A

文章编号：1672-7029(2016)05-0978-07