基于自定义本构模型的盾构隧道开挖面极限支护力研究

黄阜，李在蓝，朱亮，杨欢

(1.长沙理工大学 土木与建筑学院，湖南 长沙 410114；2.长沙理工大学 桥梁工程安全控制技术与装备湖南省工程技术研究中心，湖南 长沙 410114)

基于自定义本构模型的盾构隧道开挖面极限支护力研究

黄阜1,2，李在蓝1，朱亮1，杨欢1

(1.长沙理工大学 土木与建筑学院，湖南 长沙 410114；2.长沙理工大学 桥梁工程安全控制技术与装备湖南省工程技术研究中心，湖南 长沙 410114)

摘要:为了分析岩土体的非线性破坏特性对盾构隧道的开挖面极限支护力的影响，利用FLAC3D提供的二次开发平台，开发基于非线性Mohr-Coulomb破坏准则的自定义本构模型。调用该本构模型对盾构隧道的施工过程进行数值模拟，得到非线性M-C破坏准则作用下盾构隧道开挖面极限支护力的数值解。利用切线法将非线性Mohr-Coulomb破坏准则引入上限分析的能耗计算中，获得非线性破坏准则作用下盾构隧道开挖面支护力的上限解。通过将数值解和上限解进行对比，证明采用自定义本构模型计算的盾构隧道开挖面极限支护力是正确的。

关键词：开挖面极限支护力；非线性破坏准则；数值模拟；极限分析上限定理

自20世纪60年代我国开始筹备地铁建设至今，地铁建设在我国已经历了半个世纪的发展历程。由于地铁具备快速、环保、安全的优点，被视为解决城市交通拥堵和大气污染等问题的有效途径。因此，地铁成为目前我国基础设施建设中的热点项目，各大城市都在积极规划建设以地铁为主体的城市轨道交通体系。为了保证地铁区间隧道的开挖能够在确保安全的前提下满足工期要求，大部分地铁区间隧道都采用盾构法进行施工。盾构隧道掘进过程中，必须在开挖面上施加一个合理的支护力以保证盾构机平稳、安全地推进。当隧道开挖面即将发生失稳破坏时，作用在开挖面上的临界支护力被称为极限支护力。确定极限支护力可以为实际掘进过程中开挖面支护力大小的选择和优化提供依据。因此，盾构隧道开挖面极限支护力的研究也就成为了盾构隧道稳定性研究中的一个热点问题，国内外已经有许多学者采用各种方法对这一课题进行了卓有成效的研究。

黄正荣等[1]基于数值模拟技术，根据盾构隧道开挖面水平位移随支护力变化的关系，提出了开挖面极限支护力的确定方法，并利用这一方法研究了地下水位和土层参数对极限支护力的影响。随后，高健等[2]采用极限平衡法结合数值模拟技术对渗透力作用下的盾构隧道开挖面稳定性进行了研究。王浩然等[3]利用有限元软件，分析了盾构隧道渗流条件下的开挖面破坏模式，并在此基础上构建了开挖面的上限破坏机制，得到了渗流条件下开挖面支护力的上限解。郑永来等[4]通过构建高水压作用下的隧道开挖面破坏机制，得到了开挖面极限支护力的上限解，为越江盾构隧道支护力的确定提供了依据。Salvador等[5]在前人的研究基础上构建了一种曲线型破坏机制，在通过数值模拟技术验证了这种破坏机制的有效性之后，他们用这种破坏机制计算了盾构隧道在分层土中掘进时所需要的开挖面极限支护力。

上述针对盾构隧道开挖面极限支护力的研究都是基于线性的破坏准则进行的。然而，大量已有研究成果表明，岩土材料在破坏时，最大和最小主应力的变化遵循非线性关系。在实际工程中，采用线性破坏准则对岩土体进行研究有可能会低估土工结构的位移，因此许多学者开始采用非线性破坏准则对边坡[6-7]，地基承载力[8]，锚板[9]和土压力[10]等岩土构筑物的稳定性问题进行研究。然而，目前在相关研究中还未见采用非线性Mohr-Coulomb破坏准则构建的自定义本构模型对土工构筑物稳定性进行数值模拟的报导。因此，本文首次开发了基于非线性Mohr-Coulomb破坏准则的自定义本构模型，并通过在盾构隧道掘进的数值模拟过程中调用该本构模型，得到了非线性破坏准则作用下的盾构隧道开挖面极限支护力。然后采用极限上限法计算了盾构隧道开挖面极限支护力的上限解，通过将数值解和上限解进行对比分析，证明了将自定义本构模型应用于盾构隧道开挖面极限支护力研究的有效性。

1非线性Mohr-Coulomb本构模型

1.1非线性Mohr-Coulomb破坏准则

Agar等[11]在不同的侧限条件下对油砂进行了三轴试验，试验结果表明该砂土在破坏时，最大和最小主应力之间的非线性关系可以用下式表示：

(1)

(2)其中，c0，σt和m均为土体参数，可由三轴试验确定。1.2非线性Mohr-Coulomb本构模型的力学方程

由于非线性Mohr-Coulomb破坏准则是一个描述最大和最小主应力之间关系的幂指数型非线性函数，而广义Hoek-Brown破坏准则同样采用了幂指数型非线性函数表示最大、最小主应力之间的关系。因此，根据FLAC说明手册中Hoek-Brown本构模型的开发过程[12]，得到了用于编程的非线性M-C本构模型的力学表达式。

1.2.1基本方程

初始应力可以由弹性增量理论计算得到：

(3)

(4)

此本构模型得到的最终应力与应变增量的弹性分量有关，由此得到：

(5)

(6)

假设模型遵循如下流动法则：

(7)

(8)

模型发生屈服时的最终应力关系式为：

(9)

1.2.2流动法则

根据相关联流动法则，塑性应变率矢量应该与屈服面正交，因此：

(10)

将式(3)代入式(4)，得到了主应变增量的塑性分量，将其代入式(7)，得到：

(11)

2非线性Mohr-Coulomb本构模型在FLAC中的开发

2.1基于非线性Mohr-Coulomb破坏准则的自定义本构模型开发流程

本文利用FLAC二次开发平台VC++将非线性Mohr-Coulomb破坏准则的力学关系式嵌入到FLAC自带的本构模型的源程序中，然后生成动态链接库文件(.DLL文件)。将此文件加载到FLAC程序安装文件的根目录下，并在主程序中添加相应的调用语句，则可以随时在计算过程中根据用户指令对此本构模型进行调用。此外，用户自定义的本构模型在调用过程中与FLAC中内置的本构模型处于同一个优先级，因此采用自定义本构模型的计算效率和采用内置本构模型的计算效率一致。

2.2开发的编程概要

为了方便用户进行二次开发，FLAC软件向用户提供了内置本构模型的C++源代码，因此自定义本构模型可以在软件内置本构模型的上进行修改，而无需重新编写一个完整的自定义本构模型源程序。根据陈育民和刘汉龙[13]开发邓肯-张自定义本构模型的经验，本文在H-B本构模型的基础上将非线性M-C破坏准则的力学关系嵌入到FLAC内置的本构模型中，得到了基于非线性M-C破坏准则的自定义本构模型。自定义本构模型源程序编写的主要内容包括对内置本构模型头文件(.h)和源文件(.cpp)的修改[14]。为方便叙述，本文将自定义的本构模型命名为NonModel。

将头文件处理过程如下：

1)定义枚举函数ModelNum中的模型编号，由于FLAC软件中内置的模型较多，为避免重复，一般将模型编号取大于100。将调用模型函数以及打印输出函数中的本构模型名称均改为NonModel。

2)定义private中的私有变量。私有变量一般包括模型本身所需要的参数以及理论叙述中所使用的关键变量。考虑自定义本构模型的实际情况，将模型中的参数和重要中间变量写入其中。

编写源文件主要内容如下：

1)通过C++程序的查找功能找出源文件中含有原本构模型名称的语句并全部替换为NonModel。

2)按照头文件中的私有变量对ConstitutiveModel()函数进行相应的修改，并对头文件的私有变量赋值，通常赋值为0。

3)在properties()函数中依次将自定义本构模型的参数编写在其中，并按相同的顺序把参数写入Getproperties()函数与Setproperties()函数以及Copy()函数中。

4)根据自定义的本构模型特点，定义Initialize()函数中的关键中间变量，本函数的变量均与σ3无关，与σ3相关的变量全部写入Run()函数中。

5)确定Run()函数是整个编程中的重点与难点，其中最关键的步骤是对材料破坏准则与屈服函数的修改，具体实现过程依据前述的非线性M-C本构模型的数学表达式进行。

3基于非线性本构模型的盾构隧道开挖面极限支护力

3.1盾构隧道开挖面极限支护力的确定

为了计算非线性破坏准则作用下的盾构隧道开挖面极限支护力，利用FLAC3D构建了盾构隧道的模型，如图1所示。隧道直径6m，埋深20m，上边界取至地面，下边界取至隧道底部以下12m，横向边界取隧道两侧22m，隧道纵向长度为40m。将前述自定义本构模型的动态链接库文件复制到FLAC3D程序安装文件的根目录下，并在主程序中对这个自定义本构模型进行调用，实现非线性本构模型作用下盾构隧道开挖过程的模拟。

计算过程中，隧道一次性开挖20m，已经开挖的断面上立即施做拼装式管片衬砌，同时在开挖面上施加水平向前的支护力，并记录开挖面中心点处的水平位移。黄正荣等[1]认为，开挖面支护力不足将导致开挖面发生向盾构机压力舱的水平位移。因此，可以通过研究支护力和开挖面水平位移的关系得到开挖面的极限支护力。计算表明，开挖面的水平位移会随支护力的减小而逐渐增大，当支护力减小到某一临界点的时候，开挖面水平位移的增幅会突然变大，导致开挖面发生失稳破坏。当土体参数σt=24.7kPa，c0=10kPa，m=1.1，γ=20kN/m3时，将不同支护力对应的开挖面中心点最大水平位移记录下来，绘制成曲线图，如图2所示。从图中可以发现，当支护力减小到36.5kPa的时候，开挖面水平位移曲线出现了一个拐点，如果支护力继续减小，水平位移急剧增大导致计算不能收敛。可以认为，这个拐点对应的支护力就是维持开挖面稳定的极限支护力。

图1　盾构隧道模型Fig.1 Model of shield tunnel

图2　隧道开挖面支护力与中心点最大水平位移关系图Fig.2 Relationship between support pressure of tunnel face and the maximal horizontal displacement of center point for tunnel face

4验证计算

4.1基于非线性破坏准则的盾构隧道开挖面支护力上限解

极限分析上限定理利用构建的机动许可速度场中外力功率和内能耗散功率的关系推导出所研究问题的上限目标函数，然后通过优化计算得到该问题的最优上限解。由于上限法无需通过繁琐的弹塑性力学分析即可得到一个接近真实解的极限荷载，因而被许多学者用于盾构隧道开挖面的极限支护力研究[3, 15, 16]。为了得到主动破坏模式下盾构隧道开挖面支护力的上限解，许敬叔等[17]利用对数螺旋线构建了一种曲线型破坏机制。这种双对数螺旋线的开挖面破坏机制由两条对数螺旋线AE和BE从隧道的顶端和底部延伸到开挖面上方的土层中，交汇于E点，形成一个曲线型的二维塌落体ABE，如图3所示。O点为这个塌落体的旋转中心，该塌落体绕O点以一定的角速度ω转动。此塌落体和开挖面前方未发生位移的土体之间发生相对滑动，导致在螺旋线AE和BE上由于摩擦产生能量损耗，从而可以利用外力功率和损耗功率求解支护力的上限解。

图3　隧道开挖面对数螺旋线型破坏机制Fig.3 Logarithmic spiral failure mechanism of tunnel face

然而，许敬叔等[17]的解答是基于线性M-C破坏准则进行的，没有考虑土体非线性破坏特性对支护力上限解的影响。为了得到非线性破坏准则作用下的隧道开挖面支护力上限解，基于上述对数螺旋线型破坏机制，本文采用切线法[18-19]将非线性破坏准则引入上限定理的能耗计算过程中，得到非线性破坏准则作用下的开挖面支护力上限表达式。然后利用序列二次规划算法对该上限表达式进行优化计算，最终得到开挖面支护力的最优上限解。

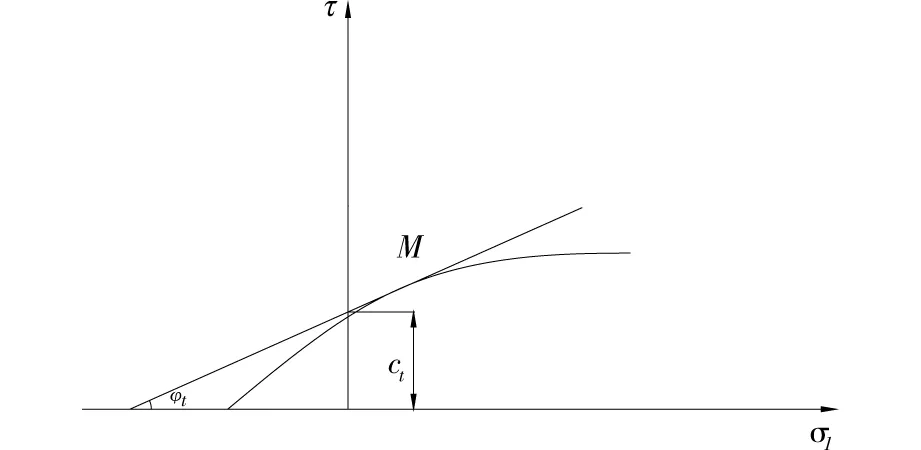
图4　M-C非线性破坏准则中的切线法Fig.4 Generalized tangential technique for M-C nonlinear failure criterion

切线法可以阐述如下：在非线性破坏准则的强度包络线上任一点M处作一条切线，则此切线在纵轴上的截距ct和其对应的倾角φt可以视为与线性破坏准则下c和φ等价的参数代入能耗计算中。图4中任一点的切线方程可由下式表示：

τ=ct+σn·tanφt

(12)

而ct和tanφt的表达式如下：

(13)

(14)

式中：c0，σt和m等参数的含义与式(2)中所示的参数一致。由于切线法中经过强度包络线M点的切线是任意的，因此在上限计算过程中，将φt视为一个变量代入上限破坏机制的能耗方程中，通过优化计算可以得到最优上限解对应的φt值和对应的切线方程。

计算开挖面支护力σT的上限解，首先要计算破坏机制中的外力功率Pe和内能耗散功率Pv，其中外力功率Pe由土体重力功率Pγ和支护力功率PT组成。利用积分运算，可以得到上述各功率的解析表达式，然后根据虚功率方程，得到隧道开挖面支护力σT上限解的表达式：

(15)

式中：ω为机动速度场中速度间断面绕旋转中心O点转动的角速度；rB为B到O点的距离；f是一个以旋转角θ为变量的函数。将式(15)视为一个目标函数，采用序列二次规划算法编制程序搜索该函数在满足相应约束条件的情况下的最大值，得到非线性破坏准则作用下的最优上限解。

4.2开挖面支护力数值解和上限解对比分析

为了验证本文采用数值模拟计算的盾构隧道开挖面支护力的正确性，将数值模拟结果和上限解进行对了比分析。利用前面所叙述的方法，当盾构隧道直径D=6m，埋深C=20m，土体参数σt=24.7kPa，c0=10kPa，γ=20kN/m3，非线性参数m=1.1～1.5时，分别计算了开挖面支护力的数值解和上限解，如下表所示：

表1开挖面支护力数值解和上限解对比

Table1Comparisonofnumericalsolutionandupperboundsolutionofsupportpressurefortunnelface

支护力σTm值1.11.21.31.41.5数值解/kPa36.545566982上限解/kPa40.550.2761.774.2387.91差值9.88%10.48%9.24%7.05%6.72%

图5　盾构隧道开挖面支护力σT随非线性参数m变化规律Fig.5 Variation law of support pressure σT for tunnel face with nonlinear parameter m

从上表中可以看出，本文计算的数值解和上限解比较吻合，最大差值为10.48%。此外，图5所示的支护力随非线性参数变化规律表明，支护力数值解和上限解随非线性参数的变化趋势相同，都随m值的增大而增大。数值解和上限解的一致性，证明利用本文所开发的自定义本构模型对盾构隧道开挖面极限支护力进行求解这一方法是正确和有效的。

5结论

1)根据非线性Mohr-Coulomb破坏准则的力学关系，利用FLAC3D提供的二次开发平台，开发了基于非线性M-C破坏准则的自定义本构模型。调用该本构模型，对盾构隧道的开挖进行数值模拟，得到了非线性M-C破坏准则作用下隧道开挖面的极限支护力。

2)采用切线法将非线性M-C破坏准则引入极限分析上限定理的能耗计算，获得了非线性M-C破坏准则作用下的盾构隧道开挖面支护力上限解。将数值模拟解和上限解进行了对比，结果表明，两者十分吻合，证明本文采用自定义本构模型计算得到的盾构隧道开挖面极限支护力是正确的。

3)参数分析表明，基于自定义本构模型计算的隧道开挖面的极限支护力，随非线性参数m的增大而增大。

参考文献：

[1] 黄正荣，朱伟，梁精华，等. 盾构法隧道开挖面极限支护压力研究[J]. 土木工程学报， 2006， 39(10): 112-116.

HUANGZhengrong，ZHUWei，LIANGJinghua，etal.Astudyonthelimitsupportpressureatexcavationfaceofshieldtunneling[J].ChinaCivilEngineeringJournal， 2006， 39(10): 112-116.

[2] 高健，张义同，乔金丽. 渗透力对隧道开挖面稳定性影响分析[J]. 岩土工程学报， 2009， 31(10): 1547-1553.

GAOJian，ZHANGYitong，QIAOJinli.Facestabilityanalysisoftunnelswithconsiderationofseepageforce[J].ChineseJournalofGeotechnicalEngineering， 2009， 31(10): 1547-1553.

[3] 王浩然，黄茂松，吕玺琳，等. 考虑渗流影响的盾构隧道开挖面稳定上限分析[J]. 岩土工程学报， 2013， 35(9): 1696-1704.

WANGHaoran，HUANGMaosong，LüXilin，etal.Upper-boundlimitanalysisofstabilityofshieldtunnelfaceconsideringseepage[J].ChineseJournalofGeotechnicalEngineering， 2013， 35(09): 1696-1704.

[4] 郑永来，冯利坡，邓树新，等. 高水压条件下盾构隧道开挖面极限上限法研究[J]. 同济大学学报(自然科学版)， 2013， 41(8): 1179-1184.

ZHENGYonglai，FENGLipo，DENGShuxin，etal.Studyonupper-boundlimitmethodoffacestabilityofshieldtunnelwithhigh-waterpressure[J].JournalofTongjiUniversity(NaturalScience)， 2013， 41(8): 1179-1184.

[5]SalvadorS,RafaelJ.Atunnelfacefailuremechanismforlayeredground,consideringthepossibilityofpartialcollapse[J].TunnellingandUndergroundSpaceTechnology, 2015(47):182-192.

[6]YANGXG,CHISC.Upperboundfiniteelementanalysisofslopestabilityusinganonlinearfailurecriterion[J].ComputersandGeotechnics. 2013(54):185-191.

[7]ZHAOLH,YANGF,ZHANGYB,etal.Effectsofshearstrengthreductionstrategiesonsafetyfactorofhomogeneousslopebasedonageneralnonlinearfailurecriterion[J].ComputersandGeotechnics, 2015(63):215-228.

[8] 张国祥，李丽民，张成平，等. 非线性破坏准则下岩石地基承载力的影响因素[J]. 土木建筑与环境工程， 2010， 32(5): 16-22.

ZHANGGuoxiang，LILimin，ZHANGChengping，etal.Factorsofbearingcapacityforrockfoundationbasedonthenonlinearfailurecriterion[J].JournalofCivil,Architectural&EnvironmentalEngineering， 2010， 32(5): 16-22.

[9] 赵炼恒，李亮，杨小礼，等. 非线性破坏准则下法向受力条形浅锚抗拔力上限计算方法[J]. 中南大学学报(自然科学版)， 2009， 40(5): 1444-1450.

ZHAOLianheng，LILiang，YANGXiaoli，etal.CalculatingmethodofupperboundforultimatepulloutcapacityofverticallyloadedstripplateanchorsbasedonnonlinearMohr-Coulombfailurecriterion[J].JournalofCentralSouthUniversity(ScienceandTechnology)， 2009， 40(5): 1444-1450.

[10]YANGXL,YINJH.Estimationofseismicpassiveearthpressureswithnonlinearfailurecriterion[J].EngineeringStructures. 2006, 28(3): 342-348.

[11]AgarJG,MorgenstemNR,SeottJ.Shearstrengthandstress-strainbehaviourofAthabascaoilsandatelevatedtemperaturesandpressure[J].CanadianGeotechnicalJournal. 1985, 24(1): 1-10.

[12]ItascaConsultingGroup.FastLagrangiananalysisofcontinuain3dimensions[M].MN,USA:ItascaConsultingGroup,Minneapolis, 2002.

[13] 陈育民，刘汉龙. 邓肯-张本构模型在FLAC～(3D)中的开发与实现[J]. 岩土力学， 2007， 28(10): 2123-2126.

CHENYumin，LIUHanlong.DevelopmentandimplementationofDuncan-ChangconstitutivemodelinFLAC3D[J].RockandSoilMechanics， 2007， 28(10): 2123-2126.

[14] 陈育民，徐鼎平.FLAC/FLAC3D基础与工程实例[M]. 北京: 中国水利水电出版社, 2013: 1-259.

CHENYumin，XUDingping.FLAC/FLAC3Dfoundationandengineeringexample[M].Beijing:ChinaWater&PowerPress, 2013:1-259.

[15] 张箭，杨峰，刘志，等. 浅覆盾构隧道开挖面挤出刚性锥体破坏模式极限分析[J]. 岩土工程学报， 2014， 36(7): 1344-1349.

ZHANGJian，YANGFeng，LIUZhi，etal.Three-dimensionallimitanalysisofblow-outfailuremodesofshallowshieldtunnels[J].ChineseJournalofGeotechnicalEngineering， 2014， 36(7): 1344-1349.

[16] 宋春霞，黄茂松，吕玺琳. 非均质地基中平面应变隧道开挖面稳定上限分析[J]. 岩土力学， 2011， 32(09): 2645-2650.

SONGChunxia，HUANGMaosong，LüXilin.Upperboundanalysisofplanestraintunnelinnonhomogeneousclays[J].RockandSoilMechanics， 2011， 32(9): 2645-2650.

[17] 许敬叔，潘秋景. 盾构隧道开挖面支护力上限分析[J]. 铁道科学与工程学报， 2014， 11(4): 80-84.

XUJingshu，PANQiujing.Upperboundanalysisofsupportingpressureforshieldtunnelfaces[J].JournalofRailwayScienceandEngineering， 2014， 11(4): 80-84.

[18]YANGXL.SeismicdisplacementofrockslopeswithnonlinearHoek-Brownfailurecriterion[J].InternationalJournalofRockMechanicsandMiningSciences. 2007, 44(6): 948-953.

[19] 赵炼恒，罗强，李亮，等. 水平矩形浅锚极限抗拔力分析[J]. 岩土工程学报， 2009， 31(09): 1414-1420.

ZHAOLianheng，LUOQiang，LILiang，etal.Ultimatepulloutcapacityofhorizontalrectangularplateanchors[J].ChineseJournalofGeotechnicalEngineering， 2009， 31(09): 1414-1420.

The study of ultimate support pressure of shield tunnelface subjected to user-defined constitutive model

HUANG Fu1,2, LI Zailan1, ZHU Liang1, YANG Huan1

(1.SchoolofCivilEngineeringandArchitecture,ChangshaUniversityofScience&Technology,Changsha410004,China;2.HunanProvinceResearchCenterforSafetyControlTechnologyandEquipmentofBridgeEngineering,ChangshaUniversityofScience&Technology,Changsha410004,China)

Abstract:To study the influence of nonlinear failure characteristics on the ultimate support pressure of shield tunnel face, the user-defined constitutive model subjected to nonlinear failure criterion was developed by using the further developing platform in FLAC3D. By invoking the constitutive model to simulate the excavation of a shield tunnel, the numerical solution of ultimate support pressure subjected to nonlinear failure criterion was obtained. Furthermore, the nonlinear failure criterion was introduced into the energy calculation by generalized tangential technique, and the upper bound solution of ultimate support pressure for shield tunnel was derived. By comparing the numerical solution and upper bound solution, the validity of ultimate support pressure calculated by user-defined constitutive model was proved.

Key words:ultimate support pressure of tunnel face; nonlinear failure criterion; numerical simulation; upper bound theorem of limit analysis

收稿日期：2015-11-25

基金项目：国家自然科学基金资助项目(51308072,51278071);长沙理工大学桥梁工程安全控制技术与装备湖南省工程技术研究中心开放基金资助项目(13KC04)；湖南省科技计划重点项目经费资助项目(2014FJ2005)

通讯作者：黄阜(1983-)，男，湖南岳阳人，讲师，博士，从事隧道与地下工程的稳定性研究；E-mail:hfcsu0001@163.com

中图分类号：TU921

文献标志码：A

文章编号：1672-7029(2016)05-0891-07