SMA弹簧-摩擦支座的滞回性能研究

庄　鹏， 薛素铎， 韩　淼， 聂　攀， 王文婷

(1.北京建筑大学 土木与交通工程学院，北京　100044；2. 北京建筑大学 “工程结构与新材料”北京高等学校工程研究中心，北京　100044；3. 北京工业大学 建筑工程学院，北京　100124)

SMA弹簧-摩擦支座的滞回性能研究

庄鹏1,2， 薛素铎3， 韩淼1,2， 聂攀1， 王文婷1

(1.北京建筑大学 土木与交通工程学院，北京100044；2. 北京建筑大学 “工程结构与新材料”北京高等学校工程研究中心，北京100044；3. 北京工业大学 建筑工程学院，北京100124)

摘要：研究一种新型形状记忆合金弹簧-摩擦支座(SMA Spring-Friction Bearing，SFB)的滞回性能。首先，研制了可用于SFB的大尺寸超弹性NiTi记忆合金(NiTi SMA)螺旋弹簧。在此基础上，加工制作了SFB试件实物模型，对其进行了拟静力试验研究。考察了竖向压力、位移幅值和加载频率对SFB恢复力-位移曲线以及等效刚度、单位循环耗能、等效阻尼比和等效动摩擦因数的影响。最后，将SMA螺旋弹簧恢复力模型和摩擦力模型相叠加，建立了SFB的恢复力模型，利用该模型进行了数值模拟。研究结果表明：SFB可提供饱满的滞回曲线，耗能能力较强，且具有一定的复位能力；数值结果与试验结果吻合较好，验证了SFB恢复力模型的正确性。

关键词：滑动隔震支座；SMA螺旋弹簧；滞回性能；拟静力试验；理论模型

隔震是一种积极有效的被动控制技术，可用于保护建筑物、桥梁以及工业设施免遭强震损害。滑动支座是一种主要的隔震装置，其中，摩擦摆支座(Friction Pendulum System)[1-3]和EQS支座(EradiQuake System)[4-5]在国内外的应用最为广泛。上述两种滑动支座在工程实践中体现出较好的隔震耗能效果，但是，二者尚存在一些不足之处，例如：摩擦摆支座由多个曲面金属部件组成，其加工制造具有一定的难度；EQS支座依靠聚氨酯弹簧提供限位、复位能力，其在恶劣环境下可能由于自身性能劣化而失效。因此，高性能滑动支座的研制仍然是科研人员和工程师所关注的重要课题之一。

形状记忆合金(Shape Memory Alloy，SMA)是一种具有独特力学性能的新型功能材料[6]。近10余年来，研究人员利用超弹性SMA的可恢复变形大(可恢复应变达到8%～10%)、滞回耗能能力出色以及耐腐蚀性能与耐久性良好等特性，将其引入到滑移隔震系统中，研制了多种含有SMA丝的可复位滑动装置。Cardone等[7]研制了一种SMA丝耗能复位装置，将其与平面滑动支座配合使用，通过现场整体试推试验检验了隔震系统在足尺三层钢筋混凝土框架结构中的响应；Dolce等[8]进一步通过振动台试验研究了该型可复位滑动支座在钢筋混凝土框架结构缩尺模型中的控制效果。在此基础上，Cardone等[9]设计了一种采用竖向布置SMA丝与平面滑动支座组成的隔震装置，并利用振动台试验考察了其有效性；Ozbulut等[10]提出了一种含有SMA丝复位装置的平面滑动支座，研究了其在桥梁结构隔震控制中的优化设计；Khodaverdian等[11]研究了一种SMA丝-滑动支座隔震系统在大型铁路桥梁中适用性。

虽然超弹性SMA丝对结构滑移隔震具有一定的控制效果，但是，小直径SMA丝材在隔震系统中的安装较为不便，其在强震作用下也容易受到损伤。近年来，大尺寸SMA的发展为结构隔震、减震提供了新的途径[12-14]。值得注意的是，大尺寸SMA螺旋弹簧可输出大位移，且能够提供较大的承载力及一定的耗能能力，可用于研发具有限位及复位功能的耗能装置[15]。基于这一思路，笔者在平面滑移隔震系统中引入大尺寸SMA螺旋弹簧，提出了SMA弹簧-摩擦支座(SMA Spring-Friction Bearing，SFB)的设计概念[16]。本文设计了一种用于水平隔震的SFB，基于拟静力试验和理论建模研究其滞回性能。首先，简要介绍了SFB的设计概念，提出了一种SFB的设计方案；进而，加工制作了SFB实物支座，对其滞回性能进行了拟静力试验研究，考察了竖向压力、加载频率、位移幅值对SFB滞回性能的影响；最后，建立了适用于整体结构分析的SFB恢复力模型，通过数值模拟对SFB恢复力模型的合理性和适用性进行了验证。

1SFB的概念设计

SFB的概念设计如图1所示，该隔震系统的主要元件包括平面滑动支座和SMA螺旋弹簧，其中，平面滑动支座可承担上部结构传递的竖向荷载，其在水平方向可通过滑动摩擦进行隔震耗能；隔震系统中的大尺寸超弹性SMA螺旋弹簧提供限位复位与辅助耗能能力。在工程应用中，可根据实际需求调整滑动支座的性能参数、SMA螺旋弹簧的数量、设置部位以及力学参数。

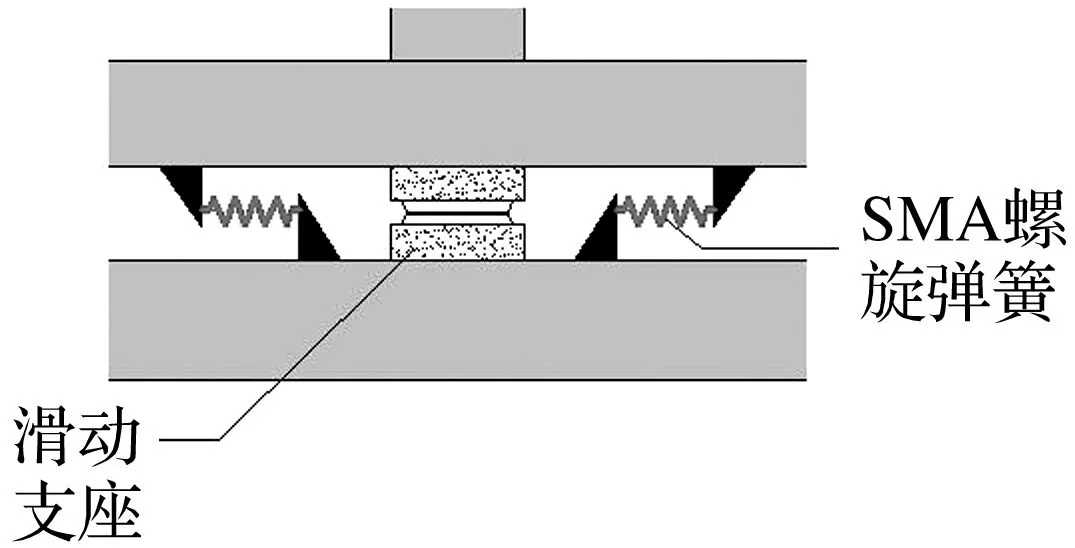
图1　SFB示意图Fig.1 Schematic diagram of SFB

2SFB的设计方案

本文提出一种SFB设计方案，该型SFB在滑块两侧对称位置平行布置2个SMA螺旋弹簧。图2给出了该型SFB的主要部件，包括：顶板、底板、滑块、滑块连接板、底板连接板以及SMA螺旋弹簧。为方便SMA螺旋弹簧的安装，将弹簧的两端处理为弯折形式，通过固定卡座进行固定后，再利用固定卡座上连接的螺杆安装于滑块连接板和底板连接板之间。当SFB进入隔震工作状态后，顶板可带动滑块在底板滑道表面水平滑动，同时带动SMA螺旋弹簧产生拉压变形。

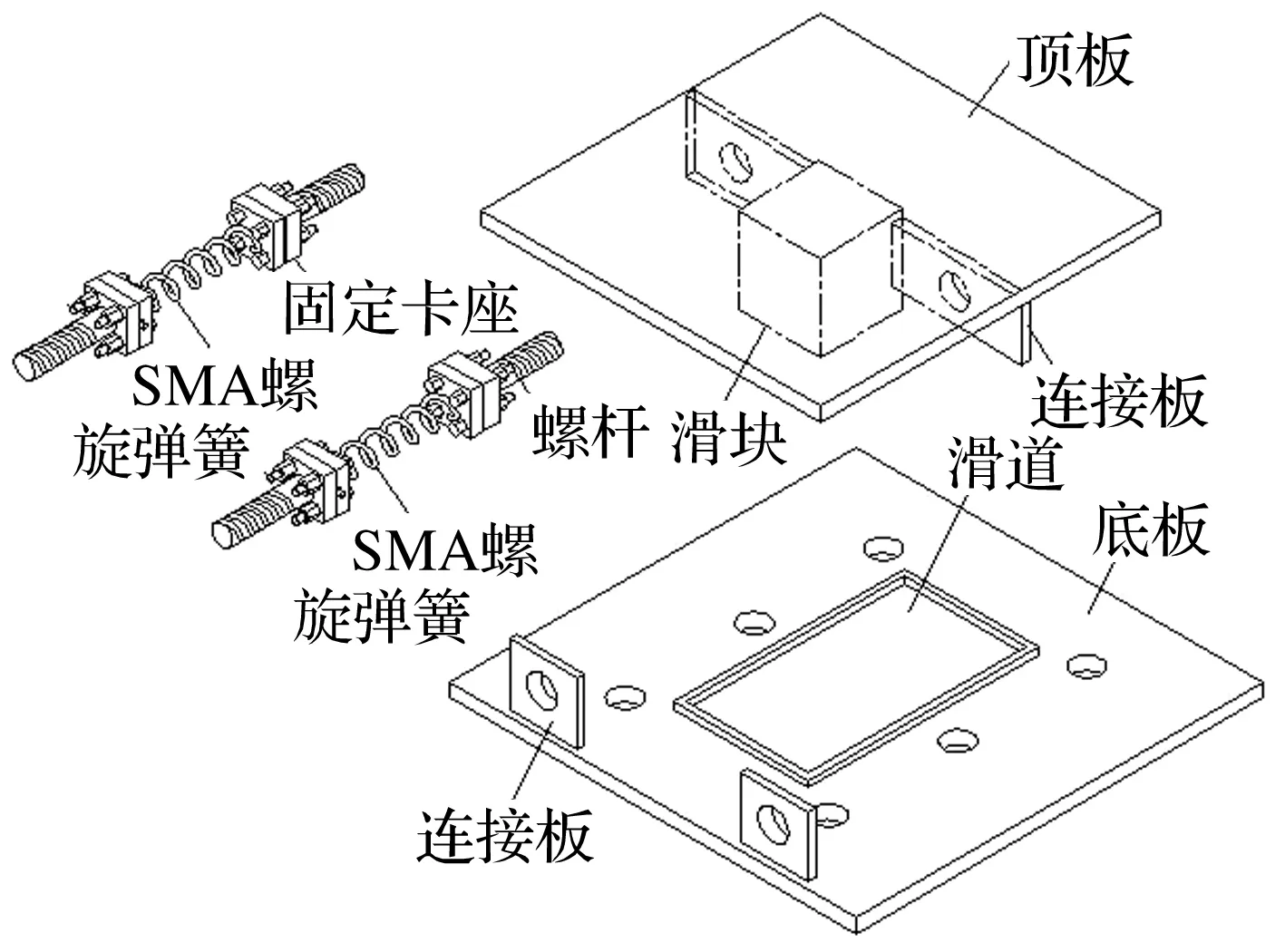
图2　SFB的主要部件Fig.2 Main component of SFB

3性能试验

3.1SMA螺旋弹簧的研制

采用化学成分为Ni50.8，Ti49.2 (原子分数，%)的NiTi记忆合金(NiTi SMA)研制大尺寸螺旋弹簧，其设计参数如下：簧杆直径为12 mm，弹簧指数为3，弹簧截距为24 mm,有效圈数为4。具有上述化学成分的SMA奥氏体相变结束温度为-12.3℃，其在室温下的初始状态为奥氏体状态，可提供超弹性效应。为考察上述SMA螺旋弹簧的力学性能，在室温状态下采用SANS微机控制电子万能试验机对其进行了单轴拉压循环力学试验。试验过程由计算机位移控制，采用三角波等频率加卸载，测试结果由计算机自动采集。SMA螺旋弹簧实物照片如图3所示。限于篇幅，本文仅给出不同位移幅值下SMA螺旋弹簧的恢复力-位移曲线(加载频率为0.1 Hz)，如图4所示。试验结果表明，SMA螺旋弹簧能够输出较大幅值的恢复力与位移，其滞回环均呈现在坐标系的一、三象限内基本对称分布的狭长梭形曲线，同时，SMA螺旋弹簧的复位性能良好。总的来看，本文研制的SMA螺旋弹簧可用作复位兼辅助耗能部件。

图3　SMA螺旋弹簧实物照片Fig.3 Photo of SMA helical spring

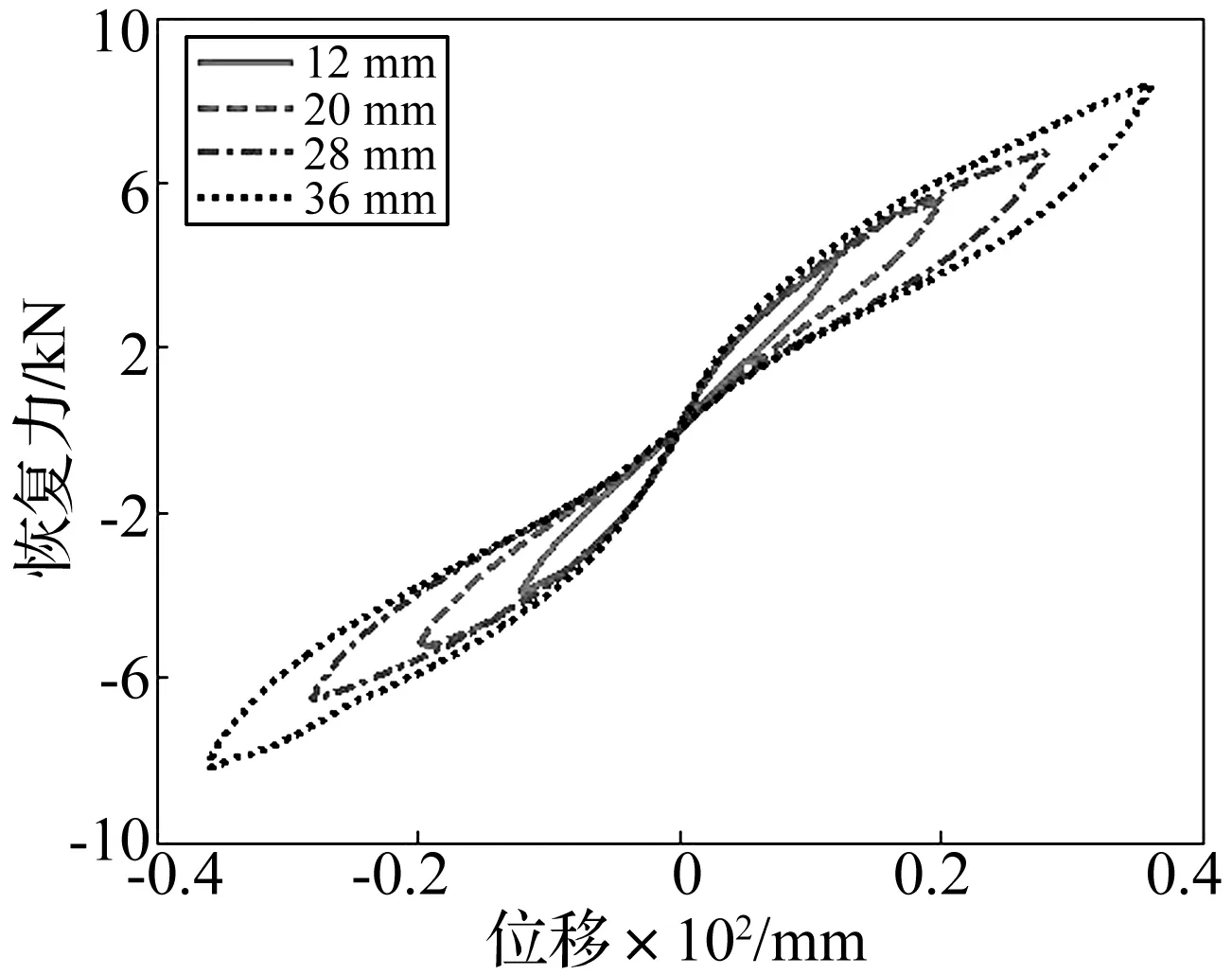
图4　SMA螺旋弹簧恢复力-位移曲线Fig.4 Force-displacement curves of SMA helical spring

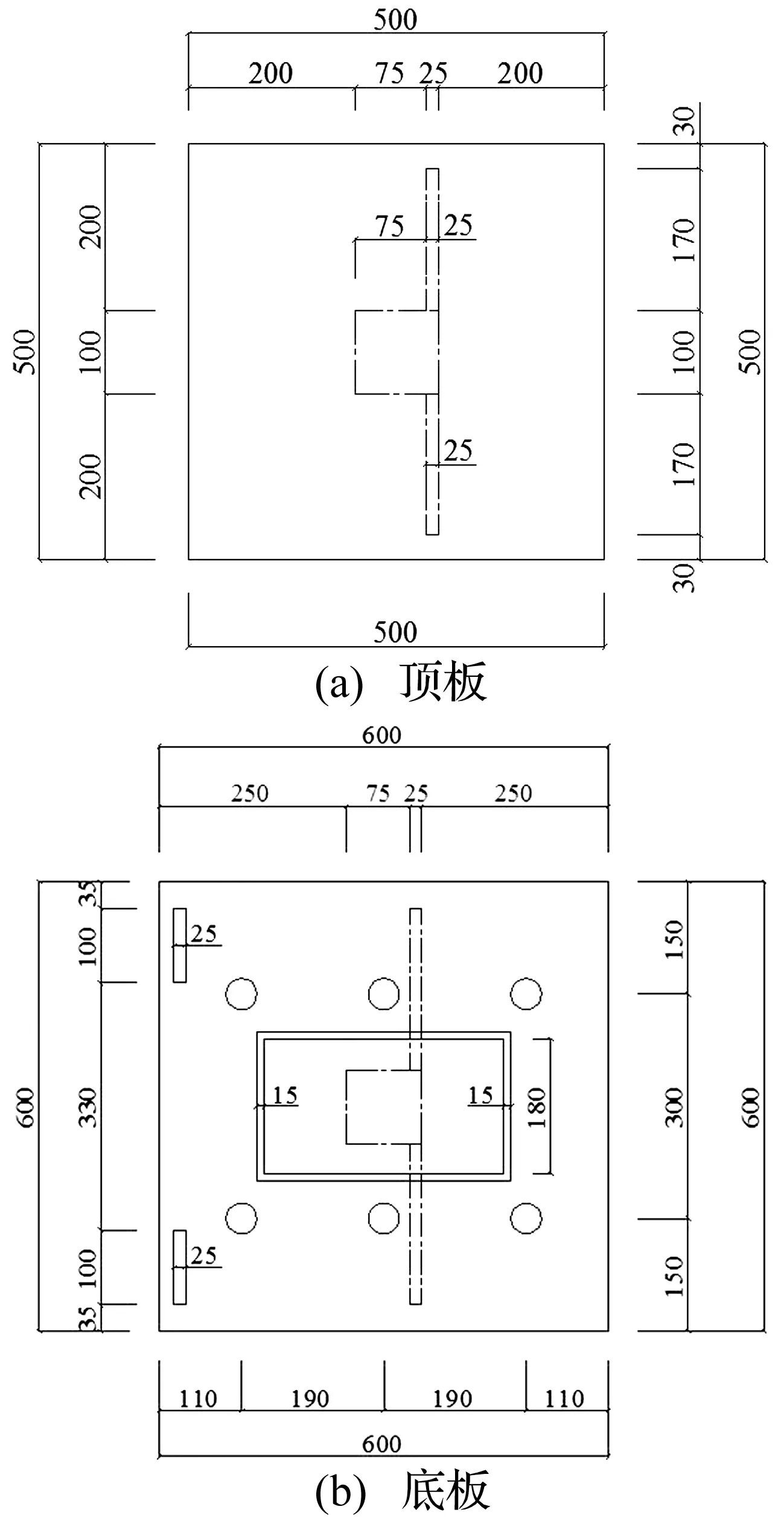
图5　SFB试件顶板和底板平面图(单位：mm)Fig.5 Plan view of top plate and bottom plate of SFB specimen (Unit: mm)

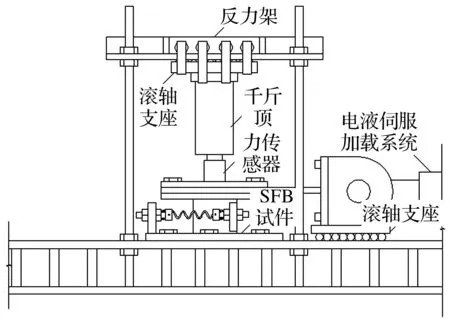
图6　试验加载装置Fig.6 Test setup

图7　SFB试件实物照片Fig.7 Photo of SFB specimen

3.2试验概况

用于试验的SFB试件顶板尺寸为500 mm×500 mm×25 mm，底板尺寸为600 mm×600 mm×25 mm，滑块为边长为100 mm的立方体；滑块底部设置Teflon板，与其接触的滑道为经过抛光后的光滑表面(不添加润滑剂)。SFB试件顶板和底板平面图如图5所示。将上文中的NiTi记忆合金螺旋弹簧用于该SFB试件。除了SMA和摩擦材料外，SFB试件其它主要部件均采用Q235钢材制作。

在安装SMA螺旋弹簧之前，使用SANS微机控制电子万能试验机对其拉压循环50次(16 mm位移幅值、0.1 Hz加载频率)，保证其滞回性能达到稳定。考虑到SMA螺旋弹簧的正常工作范围，SFB试件水平方向的设计位移为40 mm。进行试验时，通过液压千斤顶对SFB试件施加竖向压力，在水平方向采用250 kN的MTS电液伺服作动器进行加载，试验装置示意图如图6所示，SFB试件实物照片如图7所示。

本文试验目的是研究SFB试件滞回性能(滞回曲线及力学参数)随不同竖向压力、位移幅值和加载频率的变化规律。采用等频率三角波对SFB试件进行水平方向的循环加载试验，具体试验工况为：① 竖向压力分别为60 kN、80 kN和100 kN，加载频率为0.2 Hz，位移幅值为24 mm；② 位移幅值分别为20 mm、24 mm、28 mm和32 mm，竖向压力为60 kN，加载频率为0.2 Hz；③ 加载频率分别为0.05 Hz、0.1 Hz和0.2 Hz，竖向压力为80 kN，位移幅值为24 mm。以上各种工况下每次试验均连续进行5个循环。

3.3力学参数

SFB力学性能参数包括等效刚度、单位循环消耗的能量、等效阻尼比和等效动摩擦因数。

进行试验数据分析时，等效刚度Keq的计算公式为：

(1)

式中：Fmax和Fmin分别表示单次加卸载中的最大输出力和最小输出力，Dmax和Dmin分别表示单次加卸载中的最大输出位移和最小输出位移

一次水平往复荷载作用下所形成的滞回曲线面积为单位循环消耗的能量。利用上述单位循环耗能和等效刚度可计算等效阻尼比ζeq，即：

(2)

式中：Wd表示单位循环所消耗的能量。

采用等效动摩擦因数μk反映SFB的摩擦性能，其计算式[17]为：

(3)

式中：F0表示特征恢复力(滞回曲线与力轴交点对应的恢复力)，P表示支座竖向压力。

3.4试验结果及分析

SFB随不同竖向荷载、不同位移幅值和不同加载频率的恢复力-位移滞回曲线如图8所示，图中所示均为第5个循环的滞回曲线。另外，图8(b)中对应于位移幅值24 mm的滞回曲线以及图8(c)中对应于加载频率为0.2 Hz的滞回曲线均取用图8(a)中相应条件下的曲线。从图中可见，SFB在不同试验条件下均能够提供饱满的滞回曲线，具有良好的耗能能力和一定的限位复位能力。

利用图8所示滞回曲线计算SFB力学参数。不同竖向压力作用下SFB的力学性能参数如表1所示，可见，当竖向压力由60 kN变化至100 kN时，等效刚度由0.676 9 kN/mm增加到0.831 3 kN/mm，增加了22.81%；单位循环耗能由672.54 kN·mm增至935.52 kN·mm，增加了39.10%；等效阻尼比由27.45%增至31.10%，增加了16.93%；等效动摩擦因数由0.098 5降至0.087 9，减少了10.76%。不同位移幅值下SFB力学参数如表2所示，其中位移幅值为24 mm时的力学参数直接利用表1中的结果。计算结果表明，当位移幅值由20 mm增至32 mm时，等效刚度由0.729 4 kN/mm降至0.567 1 kN/mm，减少了22.25%；单位循环耗能由521.62 kN·mm增至970.31 kN·mm，增加了86.02%；等效阻尼比由28.46%降至24.92%，减少了12.44%；等效动摩擦因数变化不大，该参数由0.099 1降至0.097 7，减少了1.41%。表3给出了SFB在不同加载频率下的力学参数，其中加载频率为0.2 Hz时的力学参数直接利用表1中的结果，可以发现，当加载频率由0.05 Hz增至0.2 Hz时，等效刚度由0.747 5 kN/mm增加到0.756 6 kN/mm，增加了1.22%；单位循环耗能由761.26 kN·mm增至809.20 kN·mm，增加了6.30%；等效阻尼比由28.14%增至29.55%，增加了5.01%；等效动摩擦因数由0.090 6增至0.094 9，增加了4.53%。从表3中的结果来看，SFB力学参数取值在试验加载频率区间内较为稳定，各个工况下的力学参数变化较小。

(a) Dmax=24mm,f=0.2Hz(b) P=60kN,f=0.2Hz(c) Dmax=24mm,P=80kN图8 SFB的试验滞回曲线Fig.8TesthystereticcurvesofSFB

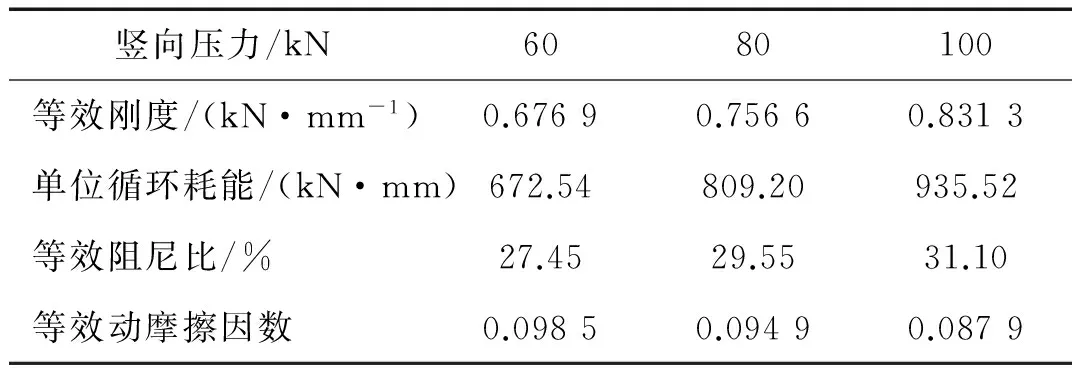
表1　不同竖向荷载下SFB的力学参数

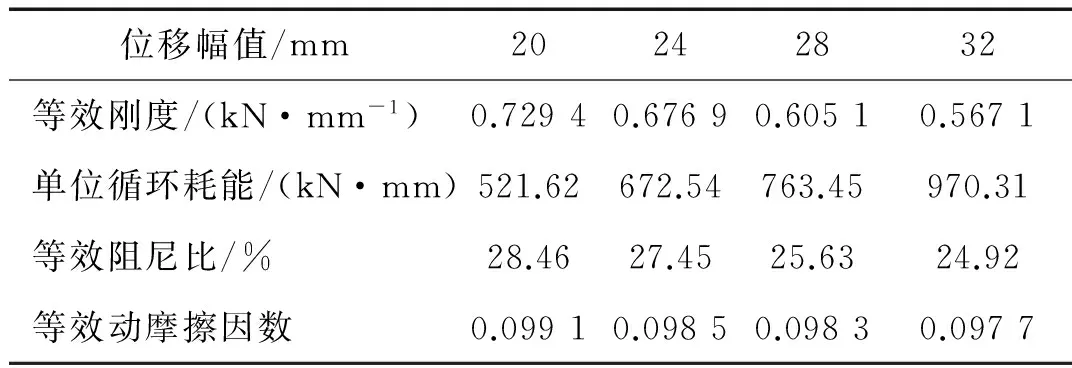
表2　不同位移幅值下SFB的力学参数

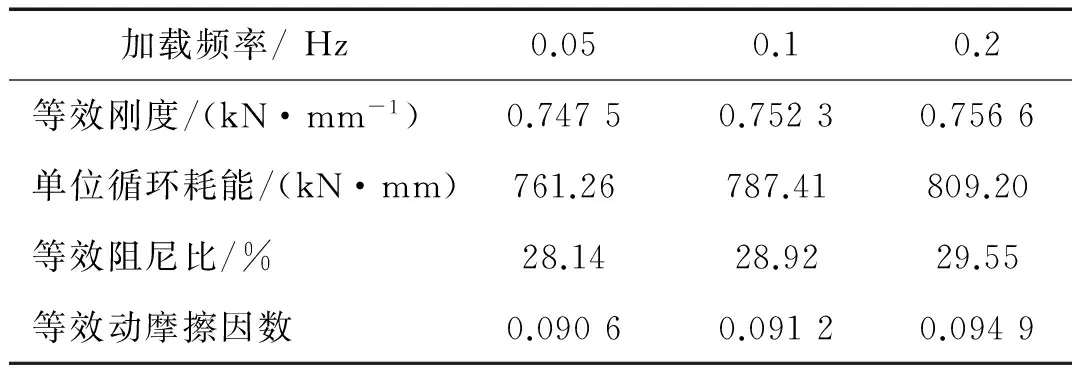
表3　不同加载频率下SFB的力学参数

4SFB恢复力模型

SFB由SMA螺旋弹簧和平面滑动支座构成，因此，装置的总体恢复力包括SMA螺旋弹簧恢复力和平面滑动支座摩擦力两部分。

对于SMA螺旋弹簧，将SMA本构关系应用于精细化有限元模型可模拟其力学行为[18]，但是，这一计算模型效率较低，难以用于整体结构的分析。为了较为便捷地模拟出光滑的恢复力-位移曲线，本文采用刚弹性恢复力模型和滞回模型进行叠加以近似模拟SMA螺旋弹簧的恢复力，即：

Fs=Fr+Fw

(4)

式中：Fs表示SMA螺旋弹簧的总体恢复力；Fr表示刚弹性恢复力；Fw表示滞回力。

在上述恢复力模型中，刚弹性恢复力模型的示意图如图9所示，其表达式为：

(5)

式中：Kr表示SMA螺旋弹簧的屈服后刚度；Fb表示位移为0时由刚弹性模型得到的恢复力；x表示位移；xd表示SMA螺旋弹簧的设计位移。

SMA螺旋弹簧超弹性恢复力中的滞回部分采用计算效率较高的Bouc-Wen模型[19]，其示意图如图10所示。该模型的表达式为：

(6)

式中：Fy表示滞回模型中的屈服力；xy表示屈服位移；α为刚度系数(屈服后刚度与初始刚度的比值)；无量纲滞回变量z满足如下微分方程：

(7)

式中：γ,β,A,n分别表示描述滞回曲线形状的无量纲参数。

由上述刚弹性模型与滞回模型合成后得到的SMA螺旋弹簧恢复力-位移模拟曲线应具有如下特征：① 模拟滞回曲线在卸载完毕时的恢复力为0；② 模拟滞回曲线中的最大恢复力与SMA螺旋弹簧试验滞回曲线中的最大恢复力相等。基于上述条件，可列出如下方程组：

(8)

式中：Fd表示试验曲线中对应于设计位移xd的恢复力。求解该方程组，可确定刚弹性模型和滞回模型中的特征参数取值。

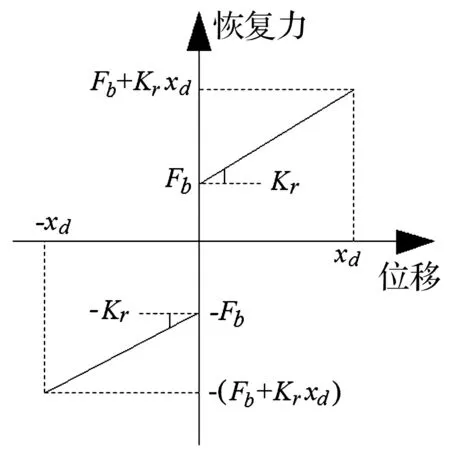
图9　刚弹性模型示意图Fig.9 Schematic diagram of rigid-elastic model

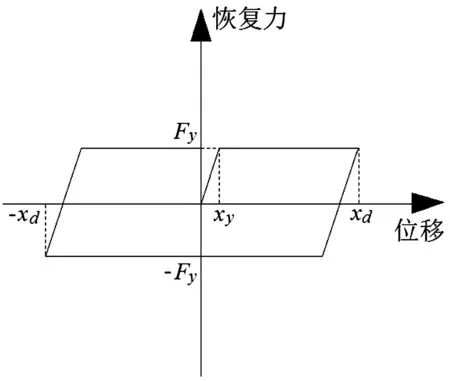
图10　滞回模型示意图Fig.10 Schematic diagram of hysteretic model

SFB中平面滑动支座摩擦力Ff的计算公式[20]如下：

Ff=μPzf

(9)

式中：μ表示滑动摩擦因数；滞回特性参数zf满足如下微分方程：

(10)

式中：Y表示滑动支座的屈服位移；ub表示滑动支座的位移；θ、λ、Ω和q分别表示控制滞回曲线形状的无量纲参数。

假设滑块两测共平行设置m个SMA螺旋弹簧，则SFB提供的侧向控制力Fis由下式计算：

(11)

式中：Fsj表示第j个SMA螺旋弹簧提供的恢复力。

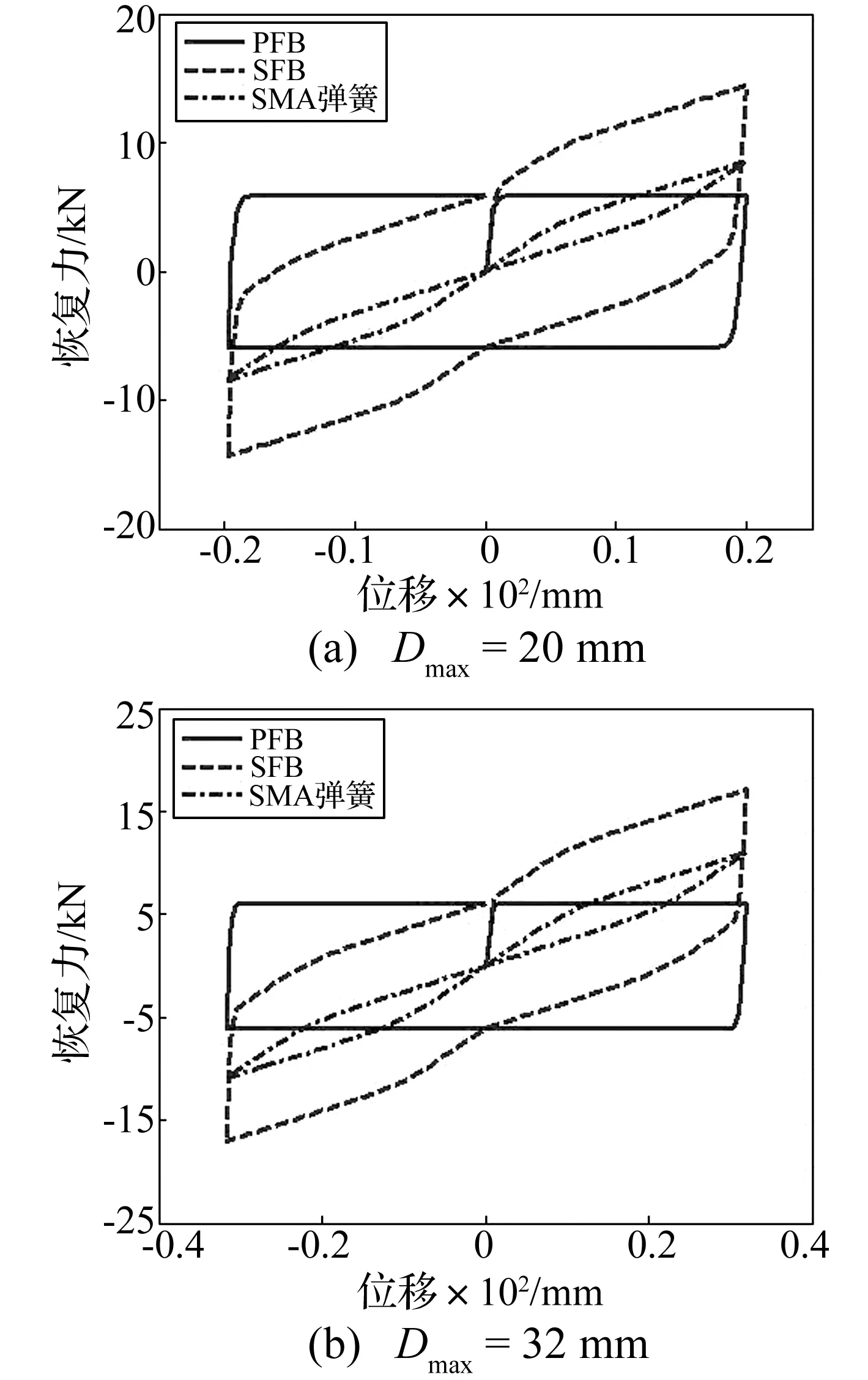
图11　SFB及其部件的模拟滞回曲线Fig.11 Simulated hysteretic curves of SFB and its components

5数值模拟结果与试验结果的对比

采用上文建立的SFB恢复力模型进行数值模拟时，需要确定SMA螺旋弹簧理论模型、平面滑动支座理论模型的特征参数取值。首先，利用12 mm、20 mm、28 mm和36 mm四种位移幅值下SMA螺旋弹簧单轴拉压循环力学试验数据，通过最小二乘线性拟合得到弹簧屈服位移xy、 屈服后刚度Kr以及每种位移幅值对

应的最大恢复力Fd的取值。进而，求解方程(8)得到特征参数Fb和Fy的取值。需要指出的是，当SMA螺旋弹簧位移幅值分别为12 mm、20 mm、28 mm和36 mm时，对应的Fb分别为0.753 3 kN、0.755 3 kN、0.733 8 kN和0.743 0 kN，而相同位移幅值下Fy的取值同Fb的取值。以上结果说明，Fb和Fy在不同位移幅值下的取值变化很小，故取其平均值用于后续的计算。SMA螺旋弹簧恢复力模型还含有刚度系数α及滞回变量z，α可取为0，而关于z的微分方程中γ、β、A和n的取值分别为0.5、0.5、1和2。此外，平面滑动支座摩擦力模型中的摩擦因数取用SFB滞回性能试验得到的动摩擦因数值，滞回变量zf计算模型中的参数取值为：Y=0.5 mm、θ=0.5、λ=0.5、Ω=1、q=2。

基于以上参数取值，编写Matlab程序进行数值计算，模拟SFB内部2个SMA螺旋弹簧提供的恢复力-位移曲线和平面滑动支座提供的摩擦力-位移曲线，将二者叠加得到SFB的总体恢复力-位移曲线。图11给出了位移幅值分别为20 mm、32 mm时平面滑动支座(Pure Flat Bearing，PFB)、SMA螺旋弹簧以及SFB的模拟滞回曲线(竖向压力为60 kN)，可见，模拟滞回曲线能够较好地描述SFB及其内部主要组件的滞回曲线形状。图12给出了部分工况下(不同竖向压力、不同位移幅值)SFB试验滞回曲线和模拟滞回曲线。从图12可以看出，SFB模拟滞回曲线与试验滞回曲线吻合较好。

图12　SFB试验与模拟滞回曲线Fig.12 Experimental and numerical hysteretic curves of SFB

竖向压力/kN等效刚度/(kN·mm-1)试验结果模拟结果误差/%单位循环耗能/(kN·mm)试验结果模拟结果误差/%等效阻尼比/%试验结果模拟结果差/%600.67690.66551.68672.54686.182.0327.4528.503.83800.75660.72624.02809.20799.021.2629.5530.422.941000.83130.77127.23935.52943.530.8631.1033.828.75

表5　不同位移幅值下力学参数试验结果与模拟结果的对比

6结论

SMA弹簧-摩擦支座(SFB)是一种新型滑动隔震支座。该支座的构造简单，竖向承载力大，耐久性好，同时，其内部SMA螺旋弹簧安装方便且易于更换。本文设计了配有两个大尺寸NiTi记忆合金螺旋弹簧的SFB，对其滞回性能进行了拟静力试验和数值模拟，得到了如下结论：

(1) 研制了适用于SFB的大尺寸NiTi记忆合金螺旋弹簧，该型SMA螺旋弹簧在室温下具有超弹性效应，可提供较为理想的滞回曲线。

(2) 在各种试验工况下SFB 呈现饱满、对称的滞回曲线，具有良好的耗能能力，且能够提供限位及复位能力，可用于工程结构的隔震控制。

(3) 随着竖向压力的增加，SFB的等效刚度、单位循环耗能和等效阻尼比增加，等效动摩擦因数有所降低；随着位移幅值的增加，SFB的等效刚度降低，单位循环耗能增加，等效阻尼比及等效动摩擦因数有小幅度的减小；加载频率对SFB滞回性能影响较小。

(4) 建立了SFB的恢复力模型，使用该模型能够较为便捷地模拟SFB的滞回曲线；力学参数的数值模拟结果与试验结果吻合较好，验证了理论模型的合理性和有效性。

参 考 文 献

[1] Zayas V,Low S,Mahin S. A simple pendulum technique for achieving seismic isolation[J]. Earthquake Spectra,1990,6(2):317-333.

[2] Mokha A,Amin N,Constantinou M,et al. Seismic isolation retrofit of large historic buildings[J]. Journal of Structural Engineering,1996,122(3):298-308.

[3] 刘彦辉,谭平,周福霖,等. 高墩隔震连续梁体地震模拟振动台试验[J]. 中国公路学报,2015,28 (2):60-68.

LIU Yan-hui, TAN Ping,ZHOU Fu-lin,et al. Shaking table test for seismic simulation of continuous isolation girder bridge with high piers[J]. China Journal of Highway and Transport,2015,28(2):60-68.

[4] Jara J,Jara M,Hernández H,et al. Use of sliding multirotational devices of an irregular bridge in a zone of high seismicity[J]. KSCE Journal of Civil Engineering,2013,17 (1):122-132.

[5] Lee H P,Kim S,Cho M S,et al. Application of sliding isolator to building structures considering cost,performance and inspection:a case study[J]. Structure and Infrastructure Engineering,2015,11 (7):851-868.

[6] Graesser E,Cozzarelli F. Shape memory alloys as new materials for aseismic isolation[J]. Journal of Engineering Mechanics,1991,117 (11):2590-2608.

[7] Cardone D,Dolce M,Ponzo F. The behavior of SMA isolation system based on a full-scale release test[J]. Journal of Earthquake Engineering,2006,10(6):815-842.

[8] Dolce M,Cardone D,Ponzo F. Shaking table tests on reinforced concrete frames with different isolation system[J]. Earthquake Engineering and Structural Dynamics,2007,36(5):573-596.

[9] Cardone D,Narjabadifam P,Nigro D. Shake table tests of the smart restorable sliding base isolation system (SRSBIS)[J]. Journal of Earthquake Engineering,2011,15 (8):1157-1177.

[10] Ozbulut O,Hurlebaus S. Optimal design of superelastic-friction base isolators for seismic protection of highway bridges against near-field earthquakes[J]. Earthquake Engineering and Structural Dynamics,2011,40 (3):273-291.

[11] Khodaverdian A,Ghorbani-Ttanha A,Rahimian M. An innovative base isolation system with Ni-Ti alloy and its application in seismic vibration control of Izadkhast bridge[J]. Journal of Intelligent Material Systems and Structures,2012,23(8):897-908.

[12] Choi E,Lee D H,Choei N Y. Shape memory alloy bending bars as seismic restrainer for bridges in seismic areas[J]. International Journal of Steel Structures,2009,9(4):261-272.

[13] 陈鑫,李爱群,左晓宝,等. 新型形状记忆合金隔震支座设计与分析[J]. 振动与冲击,2011,30 (6):256-260.

CHEN Xin,LI Ai-qun,ZUO Xiao-bao,et al. Design and study on novel shape memory isolator[J]. Journal of Vibration and Shock,2011,30 (6):256-260.

[14] 何小辉. 钢框架新型耗能梁柱节点滞回性能的研究[D]. 哈尔滨:哈尔滨工业大学,2012.

[15] Speicher M,Hodgon D,DesRoches R,et al. Shape memory alloy tension/compression device for seismic retrofit of buildings[J]. Journal of Material Engineering and Performance,2009,18 (5/6):746-753.

[16] 庄鹏,薛素铎,韩淼. SMA弹簧-摩擦支座基础隔震体系的地震响应分析[J]. 地震工程与工程振动,2015,35(2):103-113.

ZHUANG Peng,XUE Su-duo,HAN Miao. Seismic response analysis of the base isolation system using SMA spring-friction bearing[J]. Earthquake Engineering and Engineering Dynamics,2015,35(2):103-113.

[17] 张文芳,贾淑贤,李国胜. 一种全密封锁位型摩擦阻尼隔震支座的试验研究[J]. 工程力学,2009,26 (11):95-101.

ZHANG Wen-fang,JIA Shu-xian,LI Guo-sheng. Experimental researches on the slide-damping isolator with sealing cover and displacement-limited components[J]. Engineering Mechanics,2009,26 (11):95-101.

[18] Mirzaeifar R,DesRoches R,Yavari A. A combined analytical,numerical and experimental study of shape-memory-alloy helical springs[J]. International Journal of Solids and Structures,2011,48 (3/4):611-624.

[19] Wen Y K. Method for random vibration of hysteretic system[J]. Journal of the Engineering Mechanics Division,1976,102 (2):249-263.

[20] Constantinou M,Mokha A,Reinhorn A. Teflon bearing in base isolation II:modeling[J]. Journal of Structural Engineering,1990,116 (2):455-474.

Hysteretic performance of a SMA spring-friction bearing

ZHUANG Peng1,2, XUE Su-duo3, HAN Miao1,2, NIE Pan1, WANG Wen-ting1

(1. School of Civil and Transportation Engineering, Beijing University of Civil Engineering and Architecture, Beijing 100044, China; 2. Beijing Higher Institution Engineering Research Center of Structural Engineering and New Materials, Beijing University of Civil Engineering and Architecture, Beijing 100044, China; 3. College of Architecture and Civil Engineering, Beijing University of Technology, Beijing 100124, China)

Abstract:Here, hysteretic performance of a new type of isolator called shape memory alloy (SMA) spring-friction bearing (SFB) was studied both experimentally and theoretically. Firstly, large scale superelastic NiTi SMA helical springs used for SFB were developed. Then, a SFB specimen was designed and fabricated. Secondly, the quasi-static tests for SFB under different loading conditions were conducted to study the influences of vertical pressure, displacement amplitude and loading frequency on SFB hysteretic curves and mechanical parameters, such as, equivalent stiffness, energy dissipation per cycle, equivalent damping ratio and equivalent kinetic friction coefficient. Finally, combining the restoring force model of SMA spring and the model of friction force, a simplified restoring force model for SFB was established and this model was employed to simulate the hysteretic behavior of the proposed isolation device. The results showed that SFB provides full hysteretic curves, an excellent energy dissipation capacity and a certain re-centering ability; moreover, the numerical results agree well with those of tests to verify the correctness of the restoring force model for SFB.

Key words:sliding isolation bearing; SMA helical spring; hysteretic performance; quasi-static test; theoretical model

基金项目：北京市自然科学基金资助项目 (8132024); 北京市教育委员会科技计划面上项目 (KM201510016004); 北京市优秀人才培养资助项目 (2011D005017000006)

收稿日期：2015-08-28修改稿收到日期：2015-11-03

通信作者薛素铎 男，教授,博士生导师,1959年12月生

中图分类号:TU352.1; TU317.1

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.09.015

第一作者 庄鹏 男，博士,讲师,1976年7月生

E-mail:sdxue@bjut.edu.cn