数学课堂典型例题设计的有效性

吉林省延边朝鲜族自治州汪清县汪清第六中学 曹晓磊

典例，指可依为准则的成例。数学例题是帮助学生理解、掌握和运用数学概念、定理和公式的数学问题，是教师用作示范的具有一定代表性的典型数学问题，能体现数学思想，揭示数学方法，规范思考过程，无论如何改革课堂教学，都要重视课堂例题的教学。尤其在高三的复习教学中，要打造高效的数学课堂，关键的因素就是选用什么样的典型例题和如何讲解这些典型例题。

1.谈概念教学中例题的设计

概念形成环节往往是教师设计教学的主阵地，也常有独到的见解. 概念教学中的例题比较简单，因此有些教师往往忽视了例题的典型示范作用，有些布置学生自学，完全没能挖掘例题中蕴含的数学思想、方法，有些则不切实际，盲目拔高，脱离了概念的核心，其结果自然是事倍功半。例如，抛物线。

抛物线的定义是从椭圆和双曲线的第二定义引出的，采用了分类讨论的思想。2008年北京理数第4题，若点P到直线x=1的距离比它到点(2，0)的距离小1，则点P的轨迹为？

运用转化思想，将直线x=1向左平移一个单位，即直线x=2则P到直线x=2与到点(2，0)的距离相等，根据抛物线的定义，点P的轨迹是抛物线。

概念设计需灵活应用，对学生知识迁移能力要求不应过高，能很好的起到精致概念的作用。

2.谈定理教学中例题的设计

在数学里，定理是指在既有命题的基础上证明出来的命题，这些既有命题可以是别的定理，或者广为接受的陈述，比如公理。学生通过主动参与探究活动，在探究中发表意见，与他人合作，从而准确挖掘图形中隐含的条件，教师引导学生正确的得出结论。如余弦定理：

武广高铁（武广客运专线）路线规划要经过一座小山丘，就需要挖隧洞。挖隧洞就涉及到一个问题，就是要测量出山脚的长度。而两山脚之间的距离是没有办法直接测量的，那要怎样才能知道山脚的长度呢？（用PPT投影出小山丘）

技术人员的办法：工程技术人员先在地面上选一适当位置A，量出A到山脚B、C的距离，再利用经纬仪测出A对山脚BC的张角，最后通过计算求出山脚的长度BC。若测得AB=300m、AC=400m，张角A=600则BC？（配合PPT演示）问题转化为在△ABC 中已知AB=300m，AC=400m，A=600要求BC边长的的数学问题。问：这是一个解三角形的问题，那么我们可以用已学的解三角形知识解决吗？（学生很快便会发现找不到一组对边和对角无法运用正弦定理解决）定理推导：

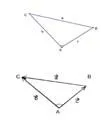
在△ABC中，设，那么，则，问题转化为已知：和b与的夹角A且

求.

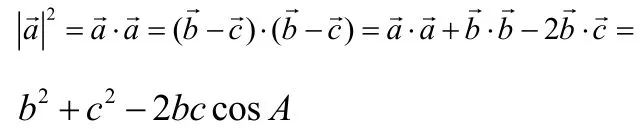
即：

从课本中应用需要出发，创设了教学中所需求的数学情境。将教材中例题作为素材改造加工成情境，是创设情境的一条有效途径。只要教师能对教材进行深入、细致、全面的研究，便不难发现教材中有不少可用的素材。

3.谈公式教学中例题的设计

公式是数学知识的精华，例题设计师公式教学中重要的一环。吃透教材，设计出少而精的具备各种功能的例题，不仅有助于学生对公式的全面理解和科学运用，更有助于学生各种能力的培养以及智力的开发。例如，在学完二倍角公式之后，我设计了下面的例题，让学生反复观察以达到熟练的程度。

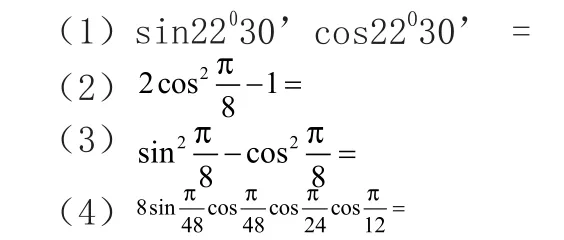
在教学中若能充分发挥类似例题的作用，能大大加快学生掌握公式的速度。

总而言之，例题设计要有针对性、趣味性，从生活中来，运用到生活中去，遵循学生思维发展规律和个体差异的原则，经过我们的归纳、提炼，努力实现例题的最优化，从而提高数学课堂的高效性。