例谈解析几何中的形异质同问题

北京市怀柔区第二中学 张 蕾

在解析几何中，经常有一些形异质同问题。虽然这些问题所描述的情景，所要解决的问题各有不同，但它们的本质却相同。解题时若能抓住这一本质，便可实现快速解题。

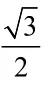
（Ⅰ）求椭圆C的方程；

（Ⅱ）证明：直线MA、MB与x轴围成一个等腰三角形。

解：（Ⅰ）设椭圆的方程

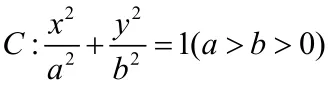
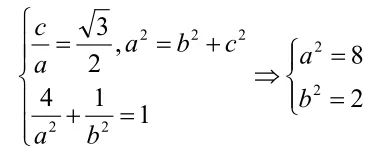
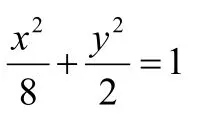
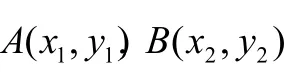
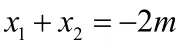
21-=mxx

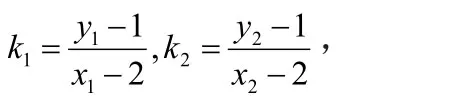
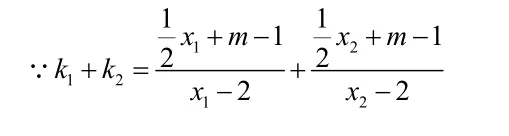
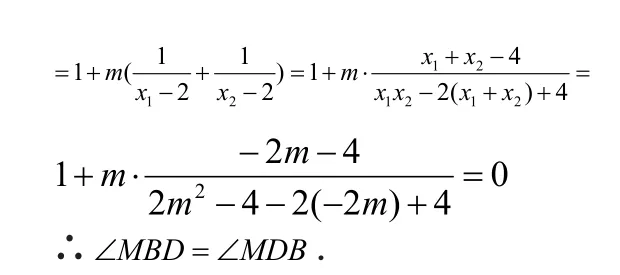
故直线MA、MB与x轴围成一个等腰三角形。

例2．如图，圆C与y轴相切于点T(0.2)，与轴x正半轴相交于两点M,N（点M在点N的左侧），且|MN|=3,

（Ⅰ）求圆的C方程；

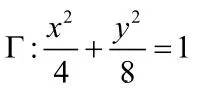
解：（Ⅰ）设圆C的半径为 )(Ar ′，依题意，圆心坐标为C′

（Ⅱ）相等，理由如下：

1．当ABx⊥轴时，由椭圆对称性可知．

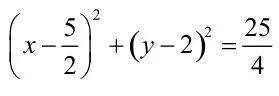
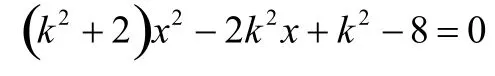
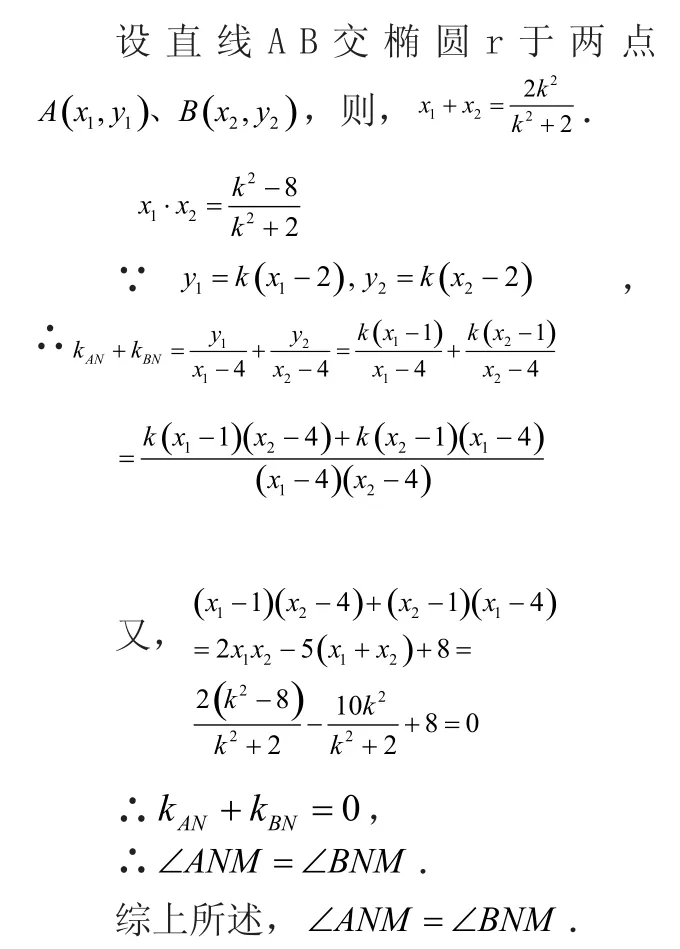
以上二题的第二问都是抓住了二个角所对应直线的倾斜角互补这一本质，进而再把证明二个角的相等问题转化为证明二个角所对应直线的斜率为互为相反数问题，从而使问题迅速得到了解决。