初中数学错题解析

四川省广元市苍溪县陵江镇第五小学校 张旭祥

【题目1】解不等式：

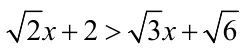
【错解】解：移项，得

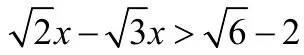
合并同类项，得

系数化为1，得

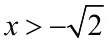
【错误分析】不等式的基本性质3没能正确运用。

【正解】 解：移项，得

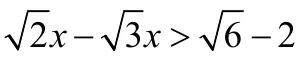
合并同类项，得

系数化为1，得x＜-

【教学反思】此题主要考查学生能否正确运用不等式的基本性质3解题。

1.教材呈现

作为教师，先要让学生熟悉这三条性质，分别是：

不等式的性质1 不等式两边都加上（或者减去）同一个数或者同一个整式，不等式的方向不变

不等式的性质2 不等式两边都乘（或者除以）同一个正数，不等式的方向不变。

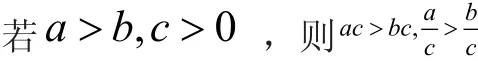
不等式的性质3不等式两边都乘（或者除以）同一个负数，不等式的方向改变。

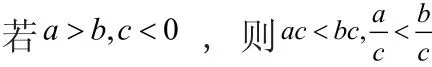
2.拓展延伸

可以这样提问：如果a＜b，a≥b ,a≤b这几种不等式在加、减、乘、除以c又会分别是什么情况？并用符号语言来阐述。

（1）若a＜b, 则a±c＜b±c

3.巧妙记忆

首先归类：可以把a＞b与a≥b归为一类， a＜b与a≤b归为一类。然后简化：通过内容观察就会发现，不等式的三条性质中，性质1 和性质2 不改变不等号的方向，只有性质3要改变不等号的方向。所以在记忆时只需记住性质3 ：即不等式两边都乘以（或除以）同一个负数时，不等号要改变方向。在这基础上还可以进一步简化为负变向。

4.解题法宝

不等式两边都加（或减去）同一个数（或式子）及乘（或除以）一个正数时，可以不作任何考虑往下做，因为不等号不会改变方向；只有在乘以（或者除以）一个负数时要特别注意要改变不等号的方向。

【题目2】 在一次数学竞赛中共有25道题，做对一道得4分，做错一道题或者有一道题没做扣一分。在这次竞赛中小明得了90分，问小明做对了多少道题？

【错解】解：设小明做对了x道题，由题意得

100-1×(25-x)=90

解得x=15

答：小明做对了15道题。

【错误分析】在解题时没有弄清题意、没有找准数量关系。

【正解】解：设小明做对了x道题，由题意得

4x-1×(25-x)=90

解得x=23

答：小明做对了23道题。

【教学反思】：此题主要考查学生列方程解应用题。

那么，怎样才能培养学生列方程解应用题的解题思维、提高学生应用题解题能力呢？

首先要让学生掌握列方程解应用题的步骤。列方程解应用题的步骤分为五步：即审、设、列、解、答。

审：即审题，弄清题意及题中的数量关系。

设:即设未知数，找出题中的未知数并用x表示，设未知数可以直接设元也可以间接设元。

列：即根据题中的数量关系列出方程。

解：即解方程。

答：即检验并写出答案。

这几个步骤在教学中怎样具体实施呢？一、培养学生的理解能力

一要对学生进行关键性词语的引导，从而让他们养成一个良好的思维落脚点的习惯，比如“比”“多”“少”“倍”“积”“商”等；

二要加强对学生专业用语的理解，保证整个解题思维不受文字的约束，比如“相向而行”，“同向而行”等等。从而使整个理解认识水平上升到一个新的高度。

二、加强学生信息整理能力

对收集得来的数据进行整理，把零碎的数学知识系统化、科学化，形成一个整体思维。

三、培养学生巧设未知数的能力

在列方程解应用题中设未知数也是一个重要的环节，怎样来设未知数，它直接关系到解应用题简便与否。如果仅靠已知量和未知量很难找到他们之间的内在联系，就应该考虑增设未知数的方法，可化难为易。

四、加强学生解应用题的步骤性

在列方程解应用题中，思维的逻辑性是必不可少的，使思维一环扣一环，既达到理清思路，又达到简洁快速的目的。

一是浏览全文，知道本应用题的基本方向和解题基本思路；

二是根据全文浏览巧设未知数，提高解题的效率；

三是返回题目，仔细阅读，并辅以画图等方式进行总结、整理信息，把实际问题转化为数学问题，形成总体思维；

四是找出等量关系（常见的等量关系见后）。根据对信息的系统化，找出题中所隐含的等量关系，为列出方程作好辅垫；

五是列出方程，解方程就是一件很容易的事情。

常见的应用题类型有：和差倍分、等积变形、相遇问题、追及问题、调配问题、比例分配问题、工程问题、利润率问题、数字问题、行船问题和销售中的盈亏问题等等，涉及到的数量关系分别有各种面积公式或体积公式、工作量=工作效率×时间、路程=速度×时间、利润=售价－进价

总之，只要掌握了列方程解应用题的步骤、找准了题中的数量关系，列方程解应用题就迎刃而解。