课堂提问要把握“四度”

山东省枣庄市峄城区古邵镇中学 白雪垠

“课堂提问”，顾名思义：在课堂教学活动中，为完成一定的教学任务，紧扣教学重点和教学难点而设计出的一系列的问题。它是教师与学生以问题为中介进行正常教学的有效方法和手段。教师科学地处理好何处提问、提什么问题、怎样提问等环节，可以帮助学生把握重点与化解难点，开启思维能力。

随着课改的深入，教师们都能注重数学课堂的提问艺术，但是一些数学课上仍发现，许多老师对以“问题”为中介的教学方式的实质理解不清晰，致使课堂提问在新课程实施过程中仍存在着较严重的偏差。然而在现实的教学过程中，提问并没有达到预期的目标。提问随意性大，一堂课多的提几十个问题，少的只提几个问题，没有针对性和推进性。提问的质量不高，缺乏艺术性，单调，没有给学生留下探究的空间，没有把课堂真正还给学生。提问的设计缺乏科学性使学生的创新思维受到抑制。可以说，这样的提问在活动中不仅不能很好地发挥提问的教育价值，而且会抑制学生的思维活动。因此，教师在教学中要精心设计有价值的问题，把握好问题的难度、梯度、密度、角度，使课堂提问更有效。下面结合具体课堂教学过程来谈谈。

一、掌握好问题的难度

怎样把握住问题的难易程度呢？一方面，要从学生的实际出发，符合学生的年龄特点和认知水平。要求以领会知识和运用知识为前提，让学生通过一定的努力能够跨越；另一方面，从教材的实际出发，教师在备课前要认真研究教材，明确教学要求，确定教学目标和重难点，因为好的提问正是紧扣教学目标和重难点提出的，让学生循序渐进，从而让他们的思维经历发现的过程，以便调动学生思维的积极性，让大多数同学经过一定的思考就能解决问题。

二、安排好问题的梯度

学习活动是一个由易到难，由简单到复杂的过程。在教学中，对于那些具有一定深度和难度的内容，学生难于理解、领悟，可以采用化整为零、化难为易的办法，把一些太复杂太难的问题设计成一组有层次，有梯度的问题，以降低问题难度。如有一位教师在讲述“二次函数的应用问题”时曾出示过这么一道题：

在一个直角三角形的内部作一个矩形ABCD，

其中AB和AD分别在两直角边上。设矩形的一边AB=xm，矩形的面积为ym2求y与x之间的函数关系式。

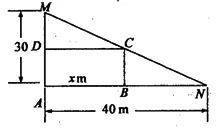
教师从出示问题到让学生回答，前后不足4分钟时间，提问时连续抽查3名同学均未能回答完整。

剖析：大多数同学看完此问题一定会感觉到漫无边际，原因是问题的设计没有遵循由易到难、由简到繁，层层递进的教学规律。问题之间缺少过渡的逻辑，因为该问题中的矩形的面积为y=AB·AD，而从已知条件中能够看出的却只有AB=x m；于是学生要解决问题的思路便陷于僵局，导致课堂氛围的不和谐。若是将原题中所问的单一问题：改为如下两问：

(1)设矩形的一边AB=x m，试用z的代数式表示AD边的长度。

(2)设矩形的面积为y rn2，求y与x之间的函数关系式。

从认知的角度上分析，全体学生都会想办法应用相似的知识将线段AD的长用x的式子表示出，然后老师将问题一环紧扣一环地连接起来，从而使学生的认识逐步深化。即可以导出结论：AD= 3 0 -x；第二问中y=AB⋅AD=x( 30 -x) = -x2+30x便可以顺理成章了。

三、调节好问题的密度

适度的课堂提问具有诊断学习、激发兴趣、集中注意、启发思维、反馈调控等教学功能.然而，如同所有真理跨过一步将会变成谬误一样，不恰当的提问必有悖于上述目的。不少课堂“问题”满天飞，师生一问一答，此起彼伏，教师提出的问题过于简单学生们不经思考就能立刻回答出来。这样的提问仅仅为了激发学生上课的“积极性”，让人感觉整节课徒有活跃的外表，华而不实，师生间的“对话”只是流于形式。如果让学生在动手实验就可以帮助学生减少盲目死记明白真正的解答。在一个问题中，老师既要听听回答正确学生的推论过程，也要判断学生的思维过程正确与否，同时也要听听答案错误学生的理由，从而寻找其错误的根源。

四、选择好问题的角度

教师的提问，应该从普遍适用的记忆性问题开始。找准联系点提问，帮助学生对知识形成多角度的理解，促进知识的广泛迁移，灵活地运用它们解决问题。启发引导学生参与知识的发生、经历探索活动的过程。“一句话十样说”，同样一个问题也有怎样问的艺术，一个问题能否激励起学生的思维，完全在于如何恰当地提出问题和巧妙地引导学生作答。

例如，我在《多边形的内角和》的教学中，用分割的思想启发学生获得n边形的内角和公式180°(n－2)的教学片断：

[师]“大家还能再用分割的方法，得到这个公式吗？”

[生1]：在多边形内任取一点，由这点向各顶点连线，有几条边就能分成几个三角形，这些三角形所有内角和为180°。由于以点p为顶点的周角不属于多边形的内角，应从中减去，从而得出n边形的内角和是180°(n－2)。

[生2]：“老师，我们有第三种方法”。

只见她在黑板上画了图，又在其中一边上取一点p，然后向各顶点连线，也得到了多个三角形，分割成的三角形的个数比边数少1，所以这些三角形所有的内角和为180°(n－1)，由于所有三角形的其中一个顶点都在点p上，组成一个平角，不属于多边形的内角，应减去，因此，多边形的内角和为180°(n－1)－180°，即为180°(n－2)。

[生3]：“我第四种方法有了！”另一位同学快步地走到黑板前，拿起粉笔在黑板上画了个多边形，在多边形的外边取了一个点p，然后从点p向各个顶点连线，这样就可以得到

(n—1)个三角形，这(n—1)个三角形的内角和为180°(n—1)，其中多出了一个三角形的内角和应减去。n边形的内角和就是：180°(n—1)-180°=180°(n－2) 。

巴尔扎克曾说过：“打开一切科学的钥匙都毫无疑义地是问号。”可见，教师如何从提问入手，以调动学生参与的积极性，激活学生的创新意识是至关重要的。课堂提问的优化是课堂教学改革中十分重要的研究课题，每一位数学教师必须高度重视课堂提问的意义，掌握和发掘课堂提问的技巧，把握课堂提问的“度”，开阔学生思路，启发学生思维，发展学生的智力和能力，促进课堂教学质量的稳步提高。