中学几何中如何灵活渗透数学思想方法

广东省梅州市丰顺县丰良中学 何彩萍

数学思想方法是数学知识内容的精髓，是对数学本质的认识，是建立数学和应用数学解决数学问题的指导思想，而作为中学几何，很多初学者都不能很好地根据题目的条件进行猜想，证明。但如果能巧用数学思想方法，则做起题目来能游刃有余。

本文结合课堂实例，说明了转化思想、整体思想、方程思想、变换思想等数学思想方法在中的巧用。

一、巧用知识，引入转化思想

转化思想就是把“陌生”的问题转化为“熟悉”的问题，把“抽象”的问题转化为“具体”的问题，把“复杂”的问题转化为“简单”的问题，如将四边形的问题转化为三角形的问题，将梯形的问题转化为三角形和平行四边形的问题来处理。

例1 如图1：已知等腰梯形ABCD中，AD‖BC，∠B=600，AD=4，BC=10,求等腰梯形的周长。

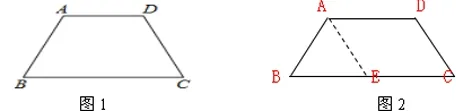
质疑启思：

（1）如何求等腰梯形的周长？

（2）由AD‖BC，再加一个什么条件便可构造一个平行四边形？

（3）∠B=600在图中有何作用？

（4）能否把AB，DC的边转化为其他同等的边？

合作探究：

（1）学生通过讨论可知要求等腰梯形的周长，除了知AD、BC长度，还要知道AB、DC的长。

（2）由AD‖BC条件，要构造平行四边形，可以作 DC‖AE，此时等腰梯形ABCD便转化为熟悉的等腰三角形和平行四边形。

（3）由∠B=600，可得等腰三角形ABE是等边三角形。

（4）因为三角形ABE是等边三角形，所以三角形ABE三条边相等，而AB、DC的长度便可转化为BE的长。而要求BE的长便可根据平行四边形条件AD=EC，BE=BC –EC=BC-AD=10-4=6得到。

解析：求等腰梯形的周长，则应求出AB、CD两腰的长，但根据已知条件我们不能直接求出，那么可以把等腰梯形转化成一个平行四边形和一个三角形来求。如图2，过点A作AE∥DC。则四边形AECD是平行四边形，所以EC=AD，从而可求出BE。又因为AE=DC=AB，∠B=60°所以△ABE是等边三角形。所以AB=BE，从而求出梯形ABCD的周长。

解：如图2：过点A作AE∥DC

因为 AD∥BC

所以四边形AECD是平行四边形

所以EC=AD，BE=BC-EC=BCAD=10-4=6

又因为AE=DC=AB，∠B=60°

所以△ABE是等边三角形

所以AB=BE=CD=6

所以梯形ABCD的周长为：

AB+BC+CD+AD=6+10+6+4=26

转化思想，是几何中最常用的一种思想方法。通过思维的转化，能提高学生的思维品质。教学中利用转化思想加以渗透，能使得学生在解决问题的过程中理解和掌握新知识，提高解决问题的能力。

二、眼观大局，引入整体思想

整体思想就是根据问题的整体结构特征，把一组图形视为一个整体去观察、分析、研究问题的一种方法，这种思想在解决与四边形相关的面积时常用到。

例2：（2009，广西桂林）如图3：在平行四边形ABCD 中，AC、BD为对角线，BC=6，BC边是的高为4,则阴影部分的面积为（ ） A 3 B 6 C 12 D 24

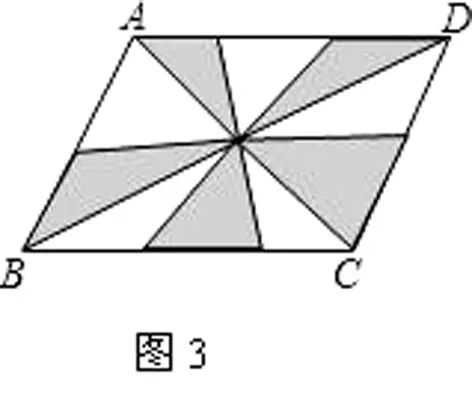
分析：根据已知条件，我们求阴影部分面积，只能将阴影部分面积看成一个整体。即把每一个阴影部分的三角形都有一个与它相对应的全等的空白的三角形，所以整个阴影部分的面积为平行四边形面积的一半：6×4÷2=12，所以选C

三、适当假设，引入方程思想

所谓方程思想，就是从问题的数量关系入手，运用数学语言将问题中的数量关系转化为方程，然后通过方程使问题得到解决。

例如，如图4，在矩形ABCD中，AB=12，BC=16，将矩形ABCD沿 CE折叠后，使点D恰好落在对角线AC上的点F处。求EF的长。

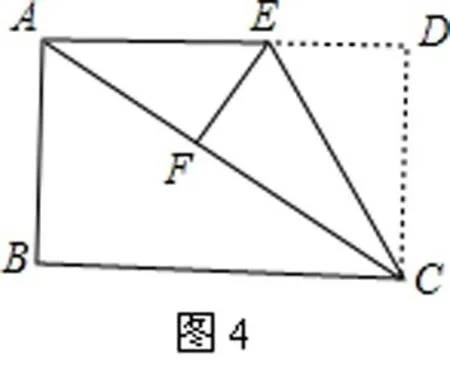
解析：要求出EF的长度，可根据矩形的性质及折叠特征，把EF放在直角三角形AEF中，根据勾股定理，由EF²+AF²=AE²可得到EF的长度，

此时设EF=x,则：

EF=ED=x，CF=CD=12，

AC==20

所以AF=AC-FC=20-12=8

在直角三角形AFE中EF²+AF²=AE²

即x ²+8²=（16- x）²

解得x =6即EF=6

四、巧妙转换，引入变换思想

几何变换思想是解决几何证明问题及几何计算中广泛应用，从运动的观点考虑，使原来静止的图形动起来，许多几何问题的已知和结论之间相互联系看起来不是很密切，但通过变换、平移、旋转等方法来构造，把图形进行运动，其中某些部分移到新的位置，使原来联系不密切的图形在新的位置产生联系，从而使问题得到解决。