CM与PSO方法评价中基性火山岩矿物组份对比

孙茹雪，潘保芝，段亚男，张　瑞

(吉林大学　地球探测科学与技术学院，长春　130061)



CM与PSO方法评价中基性火山岩矿物组份对比

孙茹雪，潘保芝，段亚男，张瑞

(吉林大学地球探测科学与技术学院，长春130061)

摘要：松辽盆地中基性火山岩具有非均质性强、矿物成分复杂以及矿物组份含量变化大等特点，这使得测井评价中基性火山岩的矿物组分含量变得十分困难。这里采用最优化方法评价中基性火山岩的矿物组分含量，将粒子群算法和复合形算法作为最优化的搜索方法，建立测井响应方程和矿物组分体积模型，对实际测井数据进行处理，求取了中基性火山岩的矿物组分含量及理论测井值。通过与岩心及薄片数据对比，复合形最优化算法的解释结果优于粒子群算法。

关键词：最优化；测井响应方程；体积模型；矿物组份

0引言

随着松辽盆地南部深层勘探取得重大突破并逐渐成为千亿方储量区后，深入开展火山岩储层的研究，是推动发现更多油气储量的重要途径[1-2]。中基性火山岩储层试气获得高产工业气流后，人们愈发重视中基性火山岩储层的研究。

由于中基性火山岩具有非均质性强、矿物成分复杂以及矿物组份含量变化大等特点，对该岩性储层参数的研究较中酸性火山岩储层少[3]。最优化方法可综合利用测井资料，计算结果比较接近实际地层，故将最优化方法引入中基性火山岩测井解释中，遗传算法最优化方法可评价储层参数，计算矿物组分含量[4]。这里以松辽盆地南部W断陷为例，针对中基性火山岩，采用粒子群与复合形两种新的最优化方法计算矿物组分含量，对比说明哪种方法更适合解释比较复杂的中基性火成岩地层。

1中基性火山岩最优化测井解释

1.1最优化测井解释方法

随着最优化测井解释技术地发展和完善，更多的专家学者对该技术进行了综合地研究。通过在旧算法的基础上研究改进出新算法，一些专家研究出了很多新型优化算法(如遗传算法、蚁群算法、粒子群算法等)，这些算法在实际中得到广泛应用。

建立最优化测井解释的理论基础是广义的地球物理反演理论，基本依据是非线性加权最小二乘原理和误差理论，以此建立最优化测井解释中的数学模型。基本原理：①通过测井资料得到能反映储层特征的经环境校正后的测井值；②根据当地的测井资料选择解释模型、测井响应方程及区域性解释参数z，经过反演算出理论测井值αi=Fi(x,z)；③将理论测井值与实际测井值进行比较，建立目标函数，当结果与实际测井资料之间的误差达到最小，x值即为最优化测井解结果[5]。最优化测井解释数学模型如式(1)所示。

(1)

其中：F(x,α)为最优化测井解释中的目标函数；x代表未知储层参数及待求矿物组份的体积含量；α是一组环境校正后的实际测井值；z为响应方程中的各个区域性解释参数；Fi(x,z)是根据解释模型而获得的第i种测井响应方程；τi是根据解释参数值获得的第i种测井响应方程误差；σi为随机误差，表示第i种实际测量中出现的测量误差；hk为等式约束条件；gJ为不等式约束条件。这样就建立了基于加权最小二乘原理的最优化测井解释目标函数。

1.2测井解释模型的建立

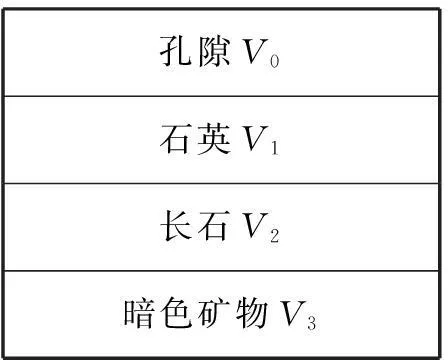
如何选择最优化测井解释模型，将直接影响测井解释结果的好坏，最优化解释可灵活采用任何测井解释模型和测井响应方程。中基性火山岩岩性复杂，矿物成分也复杂，这里选取W断陷x井火石岭组的2 573 m～2 590 m井段进行研究，该深度段的岩性为粗安质熔岩，不考虑泥质。根据研究区中基性火山岩矿物特征，建立了四种矿物含量最优化测井解释模型：孔隙、石英、长石及暗色矿物[6-8]，其中孔隙流体按100 %地层水计算，长石包含碱性长石和斜长石，暗色矿物主要为黑云母、角闪石和辉石(图1)。

孔隙V0石英V1长石V2暗色矿物V3

图1中基性火山岩测井解释体积模型

Fig.1The volume model of intermediate-basic volcanic rock logging interpretation

1.3测井响应方程的建立

根据测井解释模型，并结合地区地质经验可建立恰当的测井响应方程。这里总共选取了三条测井曲线，①补偿中子孔隙度；②密度；③声波时差曲线。将这几条经过预处理的曲线值作为实际测井值，再通过粒子群与复合形最优化算法来求孔隙流体的体积含量(V0)、石英的体积含量(V1)、长石的体积含量(V2)以及暗色矿物的体积含量(V3)，则可列出相应的测井响应方程，如式(2)、式(3)和式(4)所示。

φN=φNfV0+φN1V1+φN2V2+φN3V3

(2)

ρb=ρfV0+ρ1V1+ρ2V2+ρ3V3

(3)

Δt=ΔtfV0+Δt1V1+Δt2V2+Δt3V3

(4)

其中：φNf、φN1、φN2和φN3分别表示孔隙流体、石英、长石、暗色矿物的含氢指数值；Δtf、Δt1、Δt2和Δt3分别表示以上四种矿物的声波时差值；ρf、ρ1、ρ2和ρ3分别表示以上四种矿物的密度值。

由于各矿物体积含量之和为“1”，因而附加一个平衡方程(式(5))：

1=V0+V1+V2+V3

(5)

方程式(2)至(5)构成了一个方程组，该解可以根据粒子群与复合形最优化算法求出。故最优化测井解释问题转化为选取适当算法求下面方程组最优解的问题(式(6))：

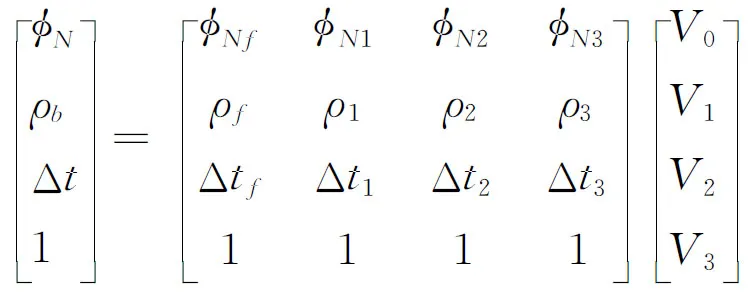
(6)

即：[T]=[R][V]其中，T为实际测井数据组，R为各个矿物组份的测井响应参数，V为待求矿物组份的体积含量。

这里建立的测井解释模型中，孔隙流体、石英、长石及暗色矿物的组份参数值可参考相关资料[9]。值得注意的是长石和暗色矿物并不是代表一种矿物，它们包含了很多种矿物，需要根据已知的参数范围，在程序中调整这些参数值的大小，当结果误差最小时，所给参数值即为最优解，此时的矿物组份参数值就确定下来了。各矿物组份参数值如表1所示。

表1W断陷中基性火山岩矿物组份测井表

Tab.1The mineral component parameter table of intermediate-basic volcanic rock in W fault depression

储层参数测井曲线中子/%密度/g·cm-3声波/μs·m-1孔隙流体1001620石英-22.65182长石-22.59140暗色矿物153147

1.4约束条件

实际应用中应该给出约束条件，以使得最优化解释结果更为可靠。一般的有数学物理约束条件、区域地质约束条件和连续性约束条件，对于求解四组分矿物组分含量，约束条件为式(7)。

(7)

1.5目标函数的建立

根据测井响应方程及约束条件，可确定目标函数。在计算时只考虑测井方法的测量误差，而测井响应方程误差不考虑。这里记中子、密度和声波的实际测井值分别为F1、F2和F3，目标函数如式(8)：

Q=(φN-f1)2/E1+(ρb-f2)2/E2+(Δt-f3)2/E3

(8)

E1、E1和E3分别表示中子测井、密度测井和声波测井的误差，本文所用曲线的测量误差取值为各个曲线的标准方差，误差值分别为1.731、0.037、8.045。

2评价中基性火山岩的矿物组份

根据最优化测井解释原理，最优化解释的基础是通过实际测井曲线，计算使得理论曲线接近实际曲线，进而求得地质参数的最佳值，作者采用了粒子群优化算法和复合形优化算法来寻优。图2为粒子群与复合形最优化测井处理流程图。

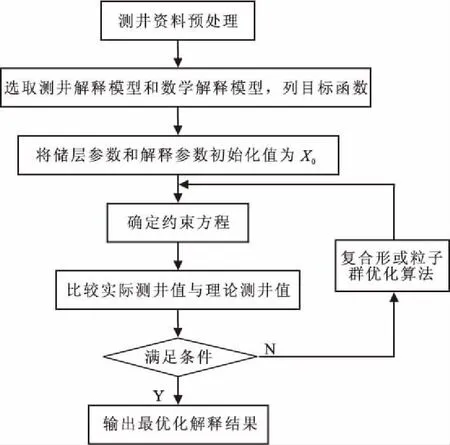
图2　PSO或CM最优化测井处理流程图Fig.2　PSO or CM optimization log processing flow chart

2.1复合形优化算法(CM)

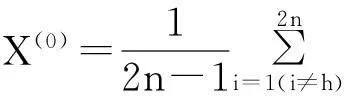
一般情况，映射点目标函数值比坏点小，此时用映射点替代坏点构成一个新的复合形。当映射点值较大时，则减小α值，直到映射点更优[10]。根据以上思想进行反复迭代循环，直到复合形收缩到各个顶点与其几何中心非常接近，同时满足迭代精度，迭代终止，最后将复合形中的最好点作为近似最优点输出。

2.2粒子群优化算法(PSO)

在粒子群优化算法中粒子通过迭代寻找最优解，算法有i个粒子，它们都是潜在解，在D维空间内群体规模(探索空间内粒子群所含粒子数)为m的粒子群，算法基本原理为：已知在维数为D的搜索空间中有i个粒子(i=1,2,…,m)飞行时，用Xi=(xi1,xi2,Λ,xiD)表示粒子的位置矢量，用Vi=(νi1,νi2,Λ,νiD)表示粒子的速度矢量。将粒子飞行过程中的曾搜索到的最优位置称为个体极值，记为pbest=(pi1,pi2,Λ,piD)，将所有粒子飞行过程中的曾搜索到的最优位置称为全局极值，记为gbest(pg1,pg2,Λ,pgd)。

粒子自身的速度与位置更新如式(9)和式(10)所示。

(9)

(10)

2.3CM和PSO最优化处理

最优化测井解释算法通过C语言编程实现的，程序中所用的矿物含量总和的约束区间在0.999～1.1之间。其中粒子群的参数选取：维数为4，即未知参数的个数；加速系数c1=c2=2；实际需要处理的数据点数为137；其最大迭代次数为10 000，初始的惯性权重系数值为0.9；终止惯性权重系数值为0.2。

3应用实例

在实际应用中，用两种算法处理了W断陷x井火石岭组的2 573 m～2 590 m井段，并计算了测井曲线的实际测井值和理论测井值之间的误差，表2为两种优化算法计算出来的测井曲线相对误差和绝对误差。

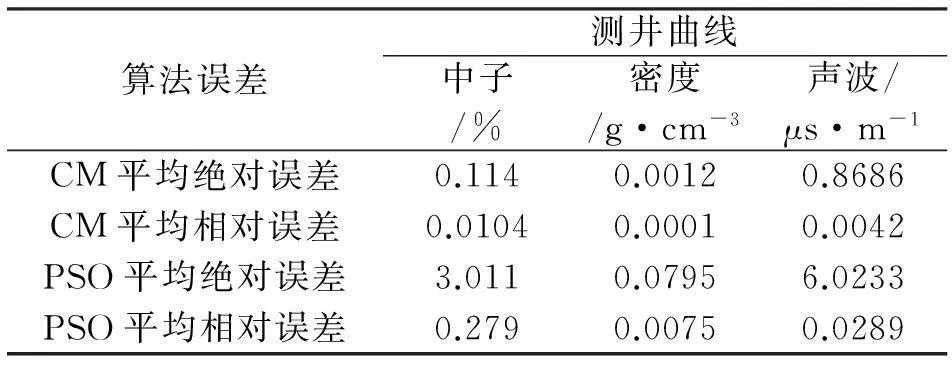
表2　最优化测井解释方法的结果误差值Tab.2　The error value of optimization logging interpretation method results

图3是补偿中子测井的理论测井值与实际测井值之间的交会图，从图3(a)中可看出，数据点大致分布在45°倾角的直线上，且数据点分布比较集中。从图3(b)中可看出,虽然数据点也是大致分布在45°倾角的直线上，但是数据点显然没有复合形算法计算出来的数据点分布集中，其结果次于复合形算法。因为中基性火山岩地区的矿物比较复杂，所以计算出的误差偏大，但是不能说明该方法不能应用于评价火山岩的矿物组分含量中。

根据岩心有效孔隙度，计算了归位后的孔隙与计算出的孔隙流体之间的误差。其中，CM平均绝对误差为0.020 2，CM平均相对误差为0.221；PSO平均绝对误差值为0.020 4，PSO平均相对误差值为0.224。计算发现，粒子群算法与复合形算法算出的矿物组分含量误差值相差不大。两种算法的综合测井图如图4所示。左面第1道为深度道，第2～4到为实际测井曲线与理论测井曲线的对比。第5道为计算出的矿物组分含量，不同的矿物组分用不同的花纹代表。右面三道分别为孔隙计算值与岩心孔隙对比，石英、长石含量与薄片分析的含量的对比，暗色矿物组分比较复杂，故没有对比。

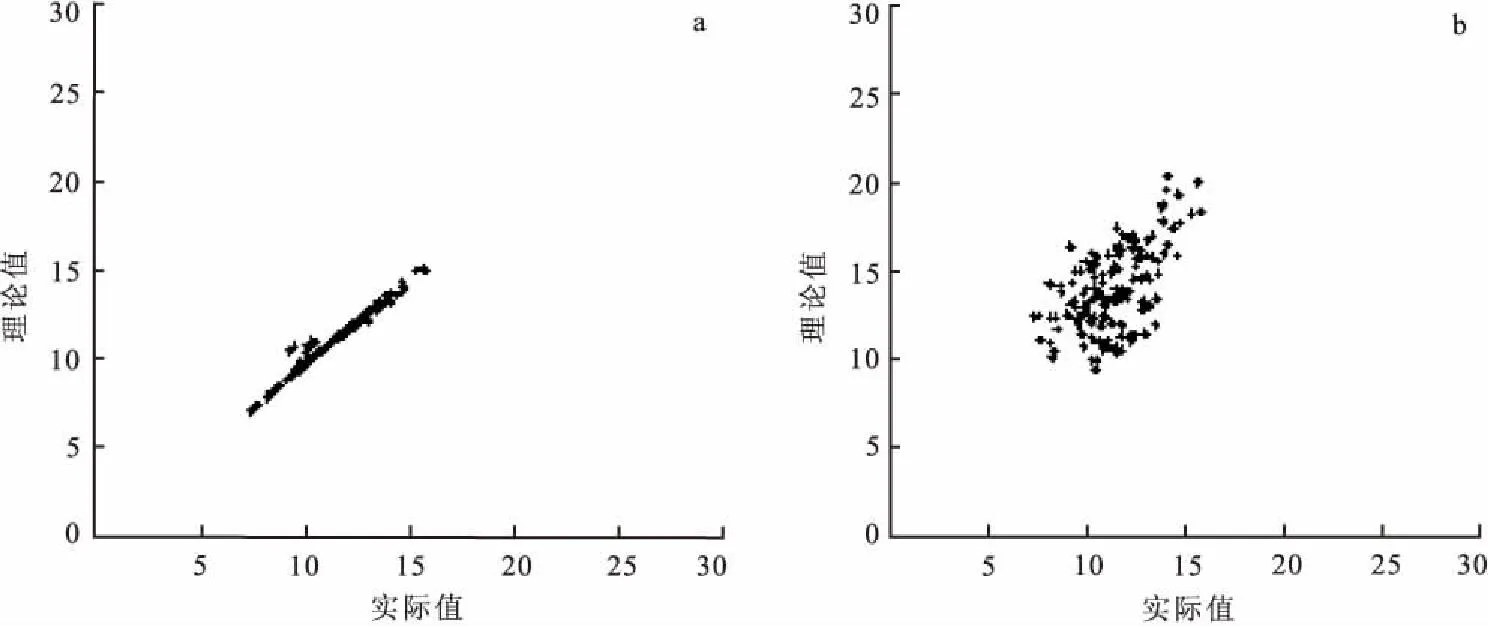
图3　最优化方法理论值与实际值的密度交会图Fig.3　The density crossplot of optimization method 's theoretical and actual value(a)CM中子交会图;(b)PSO中子交会图

复合形优化算法的结果见图4(a)，整体上各个测井的理论值与实际值曲线是比较吻合的，只有个别的点，理论与实际测井曲线有偏差，表示算法的结果是可靠的。对于石英组分含量与薄片分析吻合不是很好，计算出平均绝对误差0.102，平均相对误差为1.108。长石组分含量与薄片分析之间的平均绝对误差是0.145，平均相对误差为0.334。这说明，虽然复合形算法求出的测井曲线与实际吻合较好，但是所求矿物组分含量与薄片分析吻合较好，但还是有一定的误差。

粒子群优化算法的结果见图4(b)，通过粒子群算法计算出的理论测井曲线与实际曲线吻合程度较复合形算法差，出现一定程度的毛刺和跳跃点，但总体趋势上与实际测井曲线一致。但是对于石英、长石的组分含量与薄片分析比较吻合，石英组分含量的平均绝对误差为0.112，平均相对误差为2.434；长石组分含量的平均绝对误差为0.175，平均相对误差为0.297。综合所有的测井曲线和矿物组分含量，复合形算法的解释结果比粒子群算法要好一点，但对于不同地区不同解释人员选取的参数不同，结果也可能不一样，应用时应根据实际情况进行算法的选取。

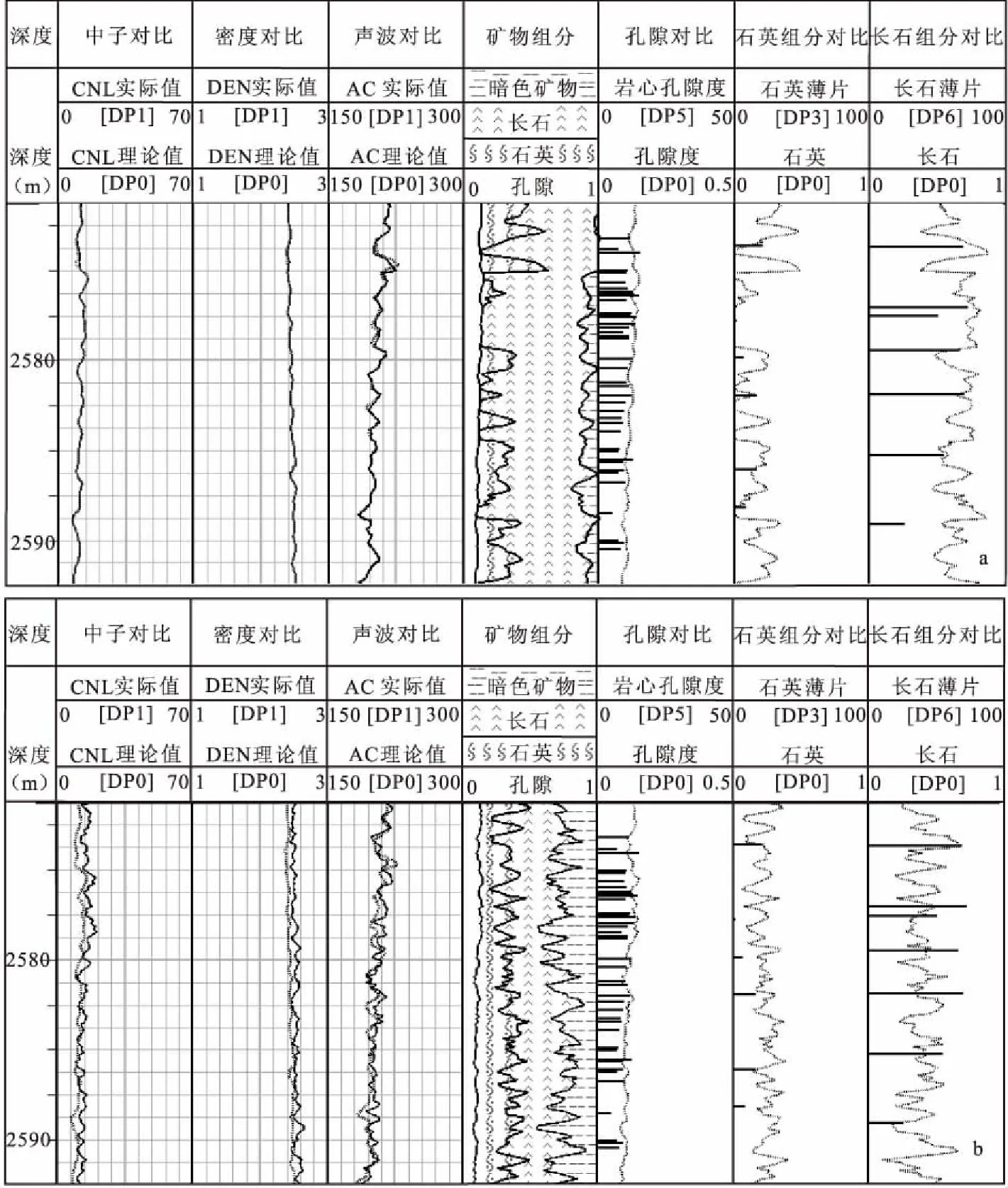
图4　x井最优化测井解释成果对比图Fig.4　The comparison figure of optimization log interpretation results in X log(a)复合形优化算法结果；(b)粒子群优化算法结果

4结论

1)中基性火山岩岩性复杂，包含石英、斜长石、碱性长石及暗色矿物等，且暗色矿物组份多样，故在建立模型上应该全面考虑，具体的组份参数值选择要依据研究区地层特点与测井资料。最优化测井解释在处理复杂的火山岩地区有独特优势，可实现几种测井方法的综合利用，通过恰当的测井解释模型和测井响应方程求取矿物的组份含量。

2)复合形算法局部搜索能力强，优化速度快，且对目标函数要求不大，计算的理论值与实际值接近，但所求矿物组分含量与实际还有偏差，原因可能是火成岩的矿物组分复杂，仅四种矿物组分含量并不能代表火山岩的实际矿物组分，这方面还需进一步研究。

3)粒子群优化算法参数简单、简便易行，且效率提高，但是容易过早收敛，发生早熟现象；出现跳跃点，该算法在参数选取上要慎重，算法仍有很大的改进空间，需要进一步研究，如果效果好便可推广到其他岩性的矿物组分分析。

参考文献：

[1]王伟锋，高斌，卫平生，等．火山岩储层特征与油气成藏模式研究[J]．地球物理学进展，2012，27(6)：2478-2491.

WANG W F,GAO B,WEI P S,et al.Research of volcanic reservoir characters and hydrocarbon accumulation models[J].Progress in Geophys,2012,27(6)2478-2491.(In Chinese)

[2]许风光，邓少贵，范宜仁，等.火成岩储层测井评价进展综述[J].勘探地球物理进展，2006，29(04)：239-243.

XU F G,DENG S G,FAN Y R，et al.Igneous rock reservoir logging evaluation review [J].Progress in exploration geophysics,2006,29(04):239-243.(In Chinese)

[3]黄玉龙.王璞君.舒萍，等.松辽盆地营城组中基性火山岩储层特征及成储机理[J]．岩石学报，2010，26(1)：82-92.

HUANG Y L.WANG P J.SHU P，et al.The Intermediate-basic volcanic rock reservoir characteristics and reservoir forming mechanism of Yingcheng Formation in Songliao Basin [J].Acta petrologica Sinica,2010,26(1):82-92.(In Chinese)

[4]王曦焓.潘保芝.遗传算法在中基性火山岩储层测井评价中的应用[J].国外测井技术，2010,(2)：38-40.

WANG X H.PAN B Z.The genetic algorithm in the application of the basic volcanic reservoir logging evaluation[J].Journal of foreign logging technology,2010(2):38-40.(In Chinese)

[5]肖亮，毛志强，孙中春，等．最优化方法在复杂岩性储集层测井评价中的应用[J]．断块油气田，2011，18(3)：342-345．

XIAO L,MAO Z Q,SUN Z C,et al.The application of optimization method in the complex lithology reservoir logging evaluation [J].Fault block oil and gas field,2011,18(3):342-345.(In Chinese)

[6]潘保芝，李周波,付有升，等．测井资料在松辽盆地火成岩岩性识别和储层评价中的作用[J]．石油物探，2009，48(01)：48-56.

PAN B Z,LI Z B,FU Y S et al.The role of logging data of igneous rock in Songliao Basin lithologic identification and reservoir evaluation [J].Geophysical Prospecting for Petroleum,2009,48(01):48-56.(In Chinese)

[7]田云英，夏宏泉.基于多矿物模型分析的最优化测井解释[J].西南石油学院学报，2006，28(4)：8-11.

TIAN Y Y,XIA H Q.Optimization logging interpretation based on analysis of multimineral model[J].Journal of Southwest Petroleum Institute,2006,28(4):8-11.(In Chinese)

[8]潘保芝，薛林福，黄布宙，等.基于QAPM矿物模型遗传算法评价火成岩储层[J]，应用地球物理，2008,5(01)：2-6.

PAN B Z ,XUE L F,HUANG B Z et al.Evaluation of volcanic reservoirs with the “QAPM mineral model” using a genetic algorithm[J].Applied Geophysics,2008,5(01):2-6.(In Chinese)

[9]斯伦贝谢测井公司.测井解释常用岩石矿物手册[M].北京：石油工业出版社，1998.SCHLUMBERGER WELL LOGGING COMPANY.Logging interpretation commonly used mineral rock manual[M].Beijing:Petroleum industry press,1998.(In Chinese)

[10]韩雪.梨树断陷砂砾岩储层GA-CM混合最优化测井解释方法研究[D].长春：吉林大学，2012.

HAN X.Research of GA -CM hybrid optimization log interpretation method about glutenite reservoir in Lishu fault depression [D].Changchun:Jilin University,2012.(In Chinese)

[11]朱丽莉，杨志鹏，袁华.粒子群优化算法分析及研究进展[J].计算机工程与应用.2007,43(5):24- 27.

ZHU L L,YANG Z P,YUAN H.Analysis and development of particle swarm optimization[J].Computer Engineering and Applications,2007,43(5):24- 27.(In Chinese)

CM and PSO method for evaluating of intermediate-basic volcanic rock mineral components comparison

SUN Ru-xue，PAN Bao-zhi,DUAN Ya-nan,ZHANG Rui

(College of geo-exploration science and technology,Jilin university,Changchun130061,China)

Abstract:Intermediate-basic volcanic rock with strong heterogeneity,complex mineral composition and mineral content of major changes in component characteristics,makes logging evaluation of intermediate-basic volcanic mineral component content difficult.In this paper,the mineral component content optimization method to evaluate the intermediate-basic volcanic rocks.The PSO and CM optimization algorithms as the search method to establish log response equation and mineral components volume model,the actual log data processing,strike the mineral component content and theoretical log values volcanic.The results are evaluated by contrasting with the core and chip data.

Key words:optimization method;logging response equation;volume model;mineral component

收稿日期：2015-03-10改回日期：2015-05-25

基金项目:国家自然科学基金(41174096)

作者简介：孙茹雪(1991-)，女，硕士，主要从事测井解释研究，E-mail:1194935521@qq.com。

文章编号：1001-1749(2016)02-0206-06

中图分类号：P 631.4

文献标志码：A

DOI：10.3969/j.issn.1001-1749.2016.02.10