谱比法的影响因素研究及应用效果分析

巫南克，周怀来,b,c

(成都理工大学 a.地球物理学院，b.“油气藏地质及开发工程”国家重点实验室，c.“地球探测与信息技术”教育部重点实验室，成都　610059)



谱比法的影响因素研究及应用效果分析

巫南克a，周怀来a,b,c

(成都理工大学 a.地球物理学院，b.“油气藏地质及开发工程”国家重点实验室，c.“地球探测与信息技术”教育部重点实验室，成都610059)

摘要：地层吸收衰减是高分辨率地震勘探面临的一大难题。品质因子Q是描述岩石弹性性质的重要参数之一，也是地层含油气性的重要标志，谱比法是实际运用中最为广泛的Q值估计方法。这里详细阐述了谱比法的基本原理，结合最小二乘拟合方法，使用雷克子波作为地震子波，从建立的理论地质模型中提取品质因子Q值，并分析了层厚度、噪声、时窗长度、拟合频带范围等因素对谱比法应用效果的影响。多层模型分析结果和实际地震资料含油气检测证明，谱比法能有效估计Q值变化情况，并能与实际钻井结果相吻合，因此运用谱比法可作为一种有效含油气检测方法。

关键词：品质因子；谱比法；影响因素

0引言

地下介质大多属于黏弹性非均匀介质，当地震波在地层中传播时，由于地层的衰减和频散引起的吸收，地震波能量的衰减随着传播距离的增加而增加，地震波的幅度和相位都会发生变化。研究地层介质对地震波的吸收，对于提高地震资料质量、高精度层析成像、反演地球物理属性和分析地下油气藏分布等都有重要意义[1-3]。品质因子Q与介质内部的结构特征和介质的饱和度、孔隙度、渗透率等流体性质都紧密相关，到目前为止出现的Q值提取方法广义上分为两类：①在时间域求取Q值的方法如子波模拟法[4]、振幅衰减法[5]、上升时间法[6-7]、解析信号法[8]等；②在频率域求取Q值的方法如频谱模拟[4]、谱比法[9]、质心频率偏移法[10-11]、峰值频率法[10-11]等。谱比法是被运用最为广泛的、最基础的Q值估计方法，由Bath[9]提出，经过多年不断研究，又有了许多谱比法的改进方法，周辉等[12]在研究谱比法计算Q值局限性的基础上，提出了一种用地震波频谱计算Q值的新方法，利用相邻两个反射子波频谱的主频及其斜率，通过Q值扫描补偿，使第二个反射信号与第一个反射信号频谱主频相同，或两者间的相似系数最大，从而计算Q值；Dasgupta等[13]用谱比法估计Q值时在叠前进行动校正避免了频谱失真从而大大提高了Q值估计的准确性;王秋成等[14]提出了均方根品质因数的计算方法，同时也将谱比法计算的约束条件放宽，将地震记录的振幅谱直接作为地震子波的振幅谱进行计算。将浅层地震波的振幅谱作为初始子波，由浅到深计算得到均方根品质因数，再利用Dix公式计算得到每一层的品质因数，通过这种改进在实际资料应用中更容易实现，且计算的结果更为稳定，也比较合理。张固澜等[15]通过对零偏移距VSP资料的监控子波和下行初至波的频谱进行综合分析，仿照Ricker子波频谱的表达式，提出了震源子波频谱新的表达式，在震源子波频谱新的表达式基础上，介绍了改进的谱比法的层Q值反演方法及相应的处理流程。谱比法虽然应用非常广泛，但是该方法依赖的因素也较多。这里详细介绍了谱比法的影响因素，通过单层模型与多层模型分析验证，并且使用实际地震资料证明谱比法的应用效果。

1基本原理

采用谱比法计算地层介质的品质因子，必须在目的层的上、下层位分别选取两个标准的反射地震子波记录段，进行频谱分析和品质因子计算。地震波在地下粘弹性介质中传播时，地震波振幅会随时间衰减，经t时刻地震波振幅可以表示为式(1)。

(1)

式中：B0(f)是初始时刻地震波的振幅谱；A(t)是与反射系数、几何扩散等因素相关的因子(与频率无关)，代表其他因素对地震波吸收衰减的影响；f是地震波的频率；t为传播时间。

将t1时刻和t2时刻地震波的振幅谱进行对比可得式(2)。

(2)

将式(2)两边同时取对数可得式(3)。

(3)

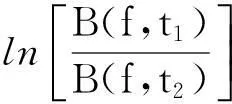
(4)

式(4)分别对a、k求偏导得：

(5)

整理得式(6)。

(6)

解方程组(6)得式(7)。

(7)

使用拟合出的斜率k，即可整理后得到求取品质因子Q的公式，如式(8)所示。

(8)

通过该方法计算出的地层Q值，为等效Q值，只与地层介质的吸收性质有关，排除了非固有衰减对Q值估计的影响[17]。

2理论模型分析

2.1单层模型

给定一个单层模型，速度V=2 500 m/s，厚度H=500 m，品质因子Q=50，选用雷克子波作为地震子波，主频30 Hz，加入高斯白噪声，研究不同因素对谱比法的影响。

2.1.1层厚度对谱比法的影响

利用谱比法对单层模型进行Q值估计得到结果如图1所示，谱比法对薄层的识别能力较差，所求得的Q值与理论值相差较大，基本没有参考价值；当地层达到一定厚度后，通过谱比法计算得到的Q值趋于稳定且与理论Q值接近。由此可见，利用谱比法对品质因子Q进行估计，对于较厚的理论模型是非常有效的。

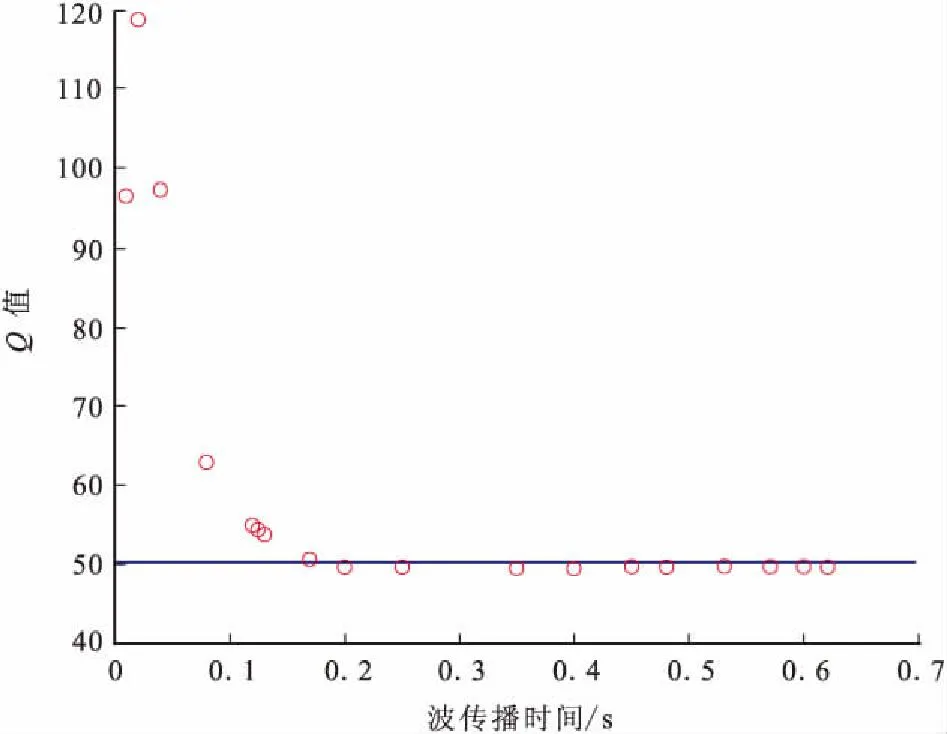
图1　地层厚度对谱比法的影响Fig.1　Effect of thickness on spectral ratio method

2.1.2噪声对谱比法的影响

在单层模型记录中分别加入信噪比(SNR)为30、10、5、0、-1的高斯白噪声，所计算出的Q值如表1所示，t为波传播时间(单位s，下同)，Mean为同一信噪比不同厚度计算得到的品质因子Q的平均值，SD为方差。随着信噪比增加，通过谱比法所求得Q值越来越稳定也更加接近理论Q值。在无噪声(或低噪声)和波干涉的情况下，通过谱比法计算得到的Q值与模型品质因子非常接近。随着地震记录中信噪比的降低，所计算的Q值变化逐渐增大，可能还会出现负值的情况，这是因为噪声叠加在有效信号上后，对振幅谱产生了影响，拟合结果强烈依赖所选择的拟合区间。由此可见，当原始数据信噪比较高时，用频谱比法计算的精度很高，计算过程引入的误差很小。

2.1.3拟合时窗长度对谱比法的影响

如表2所示，时窗长度L分别选取10 ms、30 ms、50 ms、70 ms，时窗长度的改变会对谱比法的结果造成一定影响。对于较薄的地层，时窗长度的适当增加有利于提高Q值的精度，如表2中时间t取0.12 s～0.4 s时，时窗长度从10 ms增大到30 ms和50 ms，所求得Q值精度明显提高也更加稳定。对于较厚地层，适当增加时窗长度，对谱比法求得的结果影响不明显，如表2中时间t取0.4 s～0.57 s时，时窗长度从10 ms增大到30 ms和50 ms，所求得Q值变化并不明显。在一定范围内，适当增加时窗长度，能得到更加稳定、准确的结果，但是时窗长度过长，会影响所求Q值的精度，如表2中时窗长度取70 ms时所求得数据并不能体现出所设计的理论Q值。在选取拟合时窗长度时，要结合所得资料，多次测试计算，根据振幅谱的特征以及斜率的分布找到最合理的长度。

2.1.4拟合频带范围对谱比法的影响

由于噪声等因素的影响，振幅谱之比不完全分布在一条直线上，只有合理的选取谱比法拟合频带范围，才能获得较为稳定的结果。如表3所示，频带范围F分别选取10 Hz～40 Hz、30 Hz～60 Hz、40 Hz～70 Hz，当频带范围选择10 Hz～40 Hz时，所计算得到的Q值精度最高也最稳定。在选取拟合范围时应根据实际数据的有效频带范围来确定，这样可以避免噪声干扰所带来的误差。根据实验表明，拟合区间最好选择分布在主频左右对称区间，这段区间内集中了振幅谱的主要能量，求得的Q值最稳定。

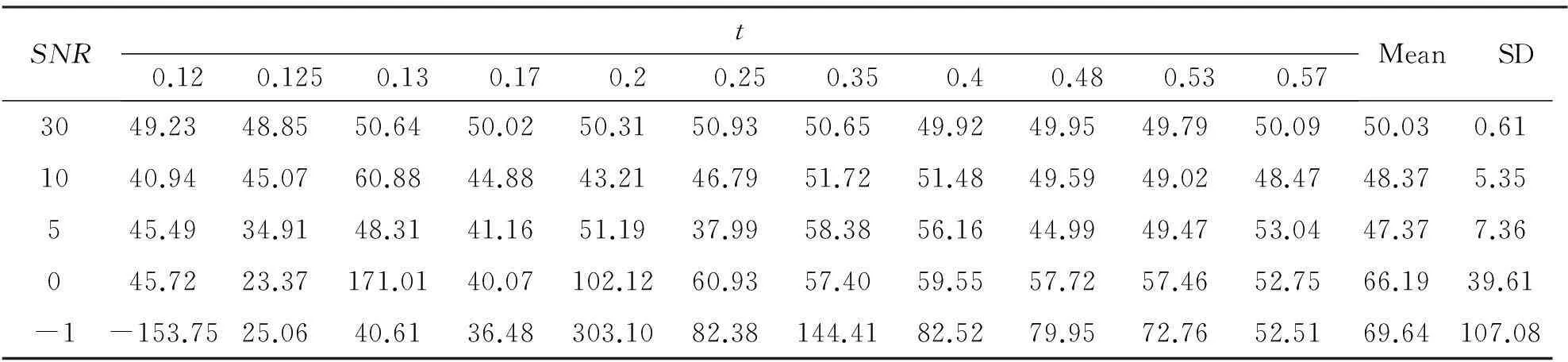
表1　不同信噪比所求得Q值Tab.1　Q for different SNR

表2　不同时窗长度所求得Q值Tab.2　Q for different time window length

表3　不同拟合频带范围所求得Q值Tab.3　Q for different frequency band

2.2多层模型

图2是一个四层介质的模型，理论Q值为30、50、100、180，层厚度分别为200 m、500 m、800 m、500 m，速度分别为1 500 m/s、1 900 m/s、2 700 m/s、3 000 m/s。图3是合成的零偏VSP地震记录，检波器间隔为20 m，一共有100道，信号采样点数为1 000，采样间隔为1 ms。震源子波用主频为30 Hz的Ricker子波模拟，加入0.1 %的随机噪声。

图2　四层模型Fig.2　Four layers of model

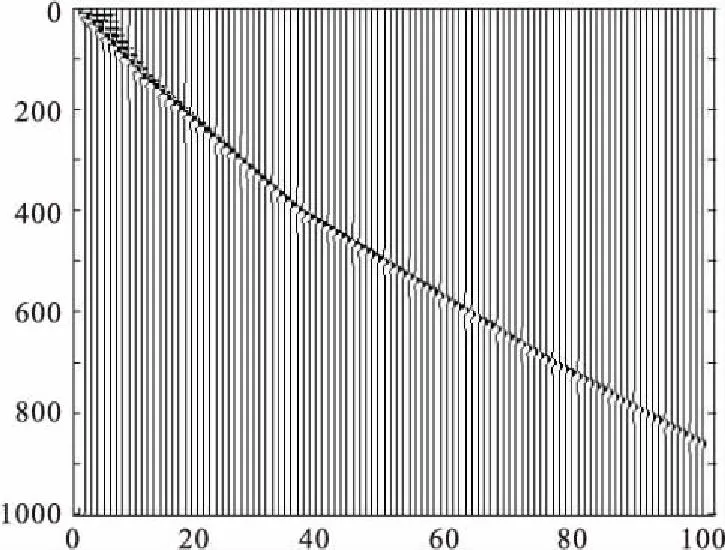
图3　合成零偏VSP地震记录Fig.3　Zero offset VSP seismic record

利用谱比法求取每相邻两道间的Q值，得到的结果如图4所示，反演结果与理论值曲线形状大致相同，但是该方法也有其不足之处，那就是它依赖的因素较多，如时窗的长度，求取斜率的起止频率等，这些因素都会导致误差的产生，随着Q值的增大，误差逐渐增大。从图5可以看出，红框范围内的点分布很不均匀，会导致拟合得到的各道斜率有一定差距，如图6所示。因此，选取适当的拟合时窗长度与频带范围，对使用谱比法稳定准确的估算Q值很重要。建立模型的时候给定了一个理论Q值，因此，可以通过调整时窗长度与频带范围等参数，使求取的结果更接近理论值。但是在实际资料处理中无法得知具体的Q值大小，而根据经验确定的时窗长度等参数往往会导致较大的误差。实验证明，该方法的稳定性不强，因此，应综合考虑多种影响因素，以达到最佳处理效果的目的。

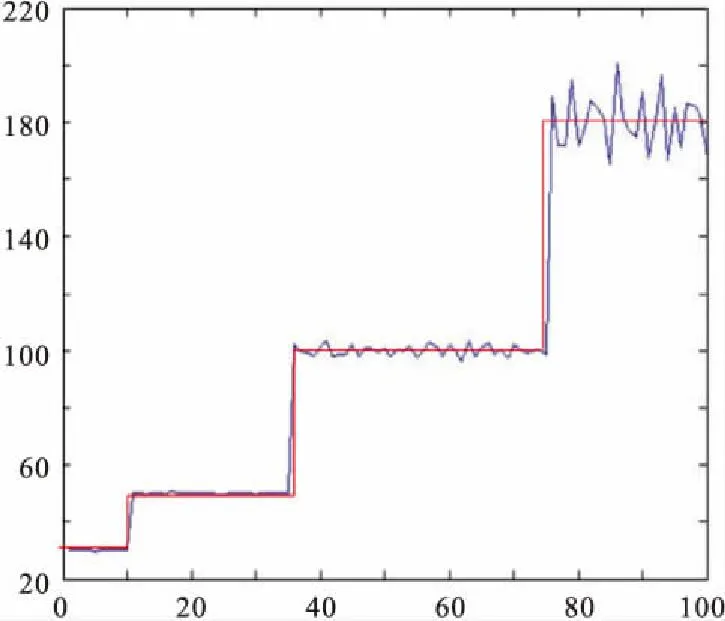
图4　计算出的Q值Fig.4　The calculated Q

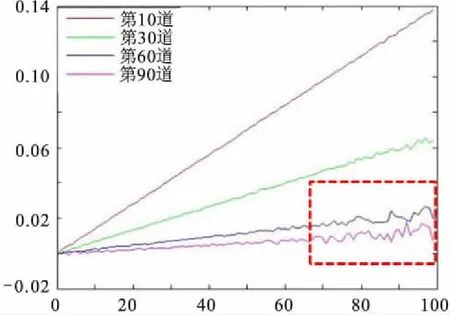
图5　振幅谱比的对数值Fig.5　Logarithm of the ratio

图6　拟合出的各道斜率Fig.6　Slope of seismic traces

3实际地震资料

为验证谱比法在实际资料处理中的可行性和稳定性，对中国西部某地区连井剖面进行Q值估计。图7为该工区A、B、C三井的连井剖面，黑线与红线为两个标志层。图8是地下实际岩性分布情况，根据三口井所反馈的信息，A与B井为高产气井、C井为干井。通过谱比法得到的Q值分布情况如图9所示，红色为低Q值，绿色为高Q值。A与B井所在位置附近的目的层为低Q值区域，且分布呈较好的成层性；C井所在位置目的层附近体现为高Q值分布区，与实际钻井信息吻合。综合以上信息可以得出，在设置合理的参数情况下，利用谱比法在油气勘探中进行储层预测是可行有效的，可作为一种有效的油气检测方法。

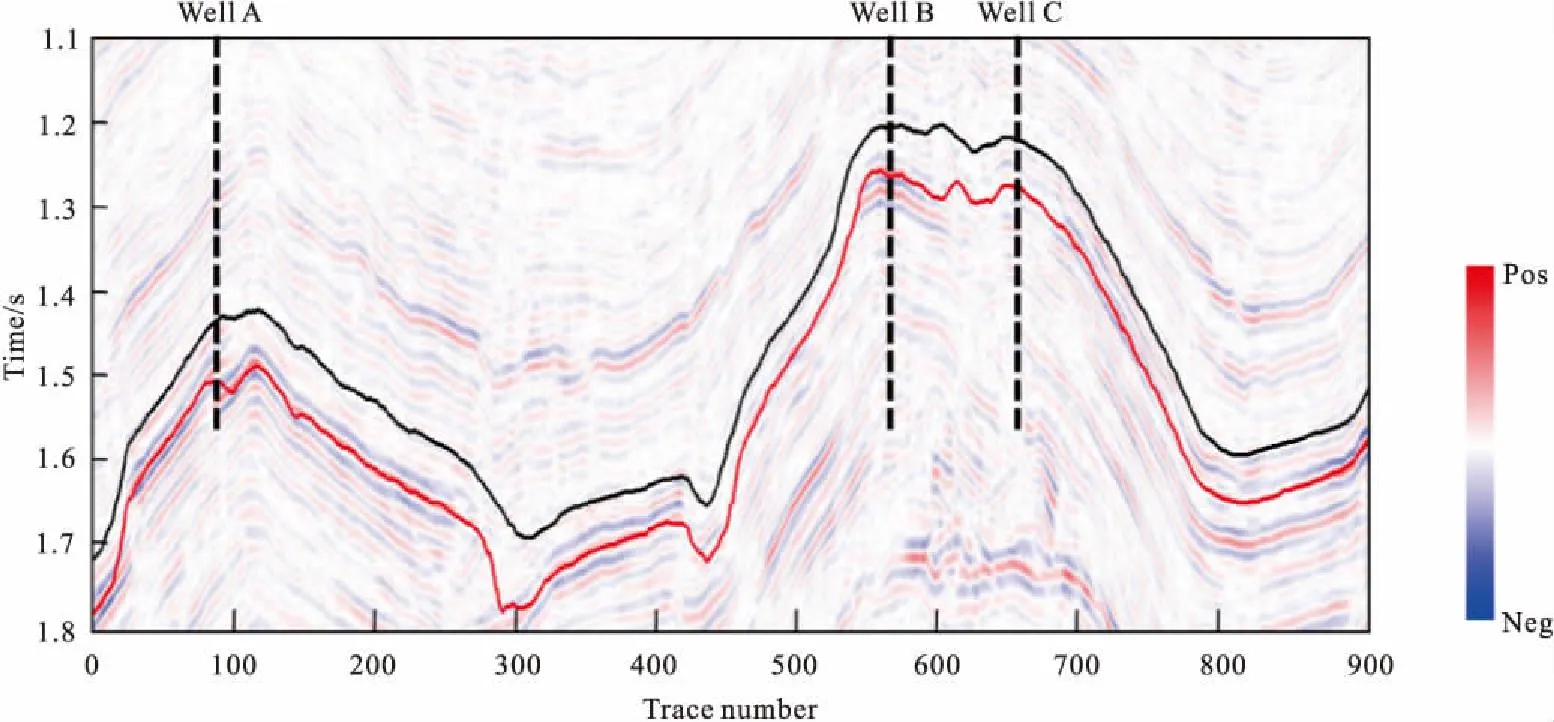
图7　A、B、C井连井剖面图Fig.7　A、B、C connecting-well section

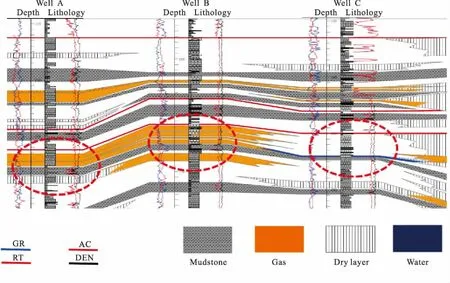
图8　岩性分布图Fig.8　Lithology distribution map

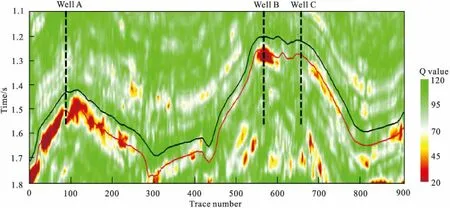
图9　Q值估计图Fig.9　The estimate of Q

4结论

本次研究中，首先通过单层模型分析了层厚度、噪声水平、拟合时窗长度和频带宽度对谱比法结果的影响，再结合多层模型和实际资料处理效果分析得出以下结论：

1)在分析薄互层条件时，时窗长度的改变对谱比法的结果造成了一定影响。实际资料无法得知具体的Q值大小，而根据经验确定的时窗长度等参数往往会导致较大的误差，因此该方法的稳定性不强，所以应根据实际资料品质加以分析，综合考虑多种影响因素来进行Q值估计，提高估计精度。

2)只有合理的选取谱比法求取斜率的频带范围和时窗长度，才能获得较为稳定、准确的结果。

3)谱比法求取介质品质因子对地震资料的品质要求很高，因此，在谱比法求取品质因子前应对数据做一些必要的去噪处理，以提高地震资料品质。

4)实际资料处理结果表明，在合理的频带范围内采用最小二乘方法进行曲线拟合，可有效提高估计精度，并能与实际钻井信息相吻合，可作为含油气检测标志。

5)Q值的精确估计是一大难题，迄今为止，没有任何一种方法适合任何情况，它们的效果很大程度上依赖于地震记录品质，因此，应在改善资料品质基础上，提高Q值估计的稳定性，特别是在薄互层估计问题上应做进一步的深入研究。

参考文献：

[1]马昭军,刘洋.地震波衰减反演综述[J].地球物理学进展,2005,20(4):1074-1082.

MA S J,LIU Y.Review of seismic waveattenuation inversion[J].Progress in Geoph-ysics,2005,20(4):1074-1082.(In Chinese)

[2]XIONG X J,HE X L,PU Y,et al.High p-recision frequency attenuation analysis and its application[J].Applied Geophysics,2011,8(4):337-343.

[3]D.JANNSEN,J VOSS,F THEILEN.Compa-rison of methods to determine Q in shallo-w marine sediments from vertical reflectio-n seismograms[J].Geophysical Prospecting,1985,33(4)：479-497.

[4]YUAN S Y,WANG S X,LUO C M,et al.Simultaneous multitrace impedance inversion with transform-domain sparsitypromotion [J].Geophysics,2015,80(2):R71-R80.

[5]孙成禹.地震波理论与方法[M].东营:中国石油大学出版社,2007.

SUN C Y.Seismic wave theory and meth-od[M].Dongying:China Univer-sity of Petroleum press,2007.(In Chinese)

[6]P G KELAMIS,E KJARTANSSON.Forward modeling inthe Frequency-Spacedomain.G-eophysical Prospecting,1985,33(2):252-262.

[7]KJARTANSSON E.Constant Q-wave propagation and attenuation[J].Journal of Geop-hysical Research,1979,84:4737-4748.

[8]M T TANER,F KOEHLER,R E SHERIFF.Complex seismic trace analysis[J].Geophy-sics,1979(6):1041-1063.

[9]BATH M .Spectral Analysis in Geophys-ics[M].New York:Elsevier,1974.

[10]TONN R.七种计算Q值方法的比较[J].郑需要，译.世界地震译丛,1992,4:77-83.

TONN R.Comparison of seven methods forcalculating Q[J].ZHENG X Y translate.Wo-rld earthquake series,1992,4:77-83.(In Chinese)

[11]聂冀强．零偏VSP资料的Q值反演方法及应用[D]．北京:中国地质大学,2011.

NIE J Q.Interval Q inversion based on zero—ofset VSP data and application[D].Beijing:China University of Geosciences,2011.(In Chinese)

[12]周辉，渠广学，杨宝俊.用地震波频谱计算Q值的新方法[J].长春:长春地质学院学报,1994,24(4):461-467.

ZHOU H,QU G X,YANG B J.New meth-od for calculating Q by using seismic wa-ve spectrum[J].Changchun:Journal of Changchun Institute of Geology,1994,24(4):461-467.(In Chinese)

[13]DASGUPTA R,CLARKZ R A.Estimation of Q from surface seismic reflection data[J].Geophysics,1998,63(12):2120-2128.

[14]王秋成，李培明，何宝成.改进谱比法在实际资料吸收衰减分析中的应用[C].深圳:SPG/SEG国际地球物理会议论文集,2011,151:131-134.

WANG Q C，LI P M，HE B Q.The improved spectral ratio method in the actual data analysis in the application of attenuation[C].Shenzhen:SPG/SEG International geophysical conference proceedings,2011,151:131-134.(In Chinese)

[15]ZHANG G L,WANG X M.Interval Q inversion based on zero—ofset VSP data andapplicatio-n.Applied Geophysics,2014,11(2)：235—244.

[16]PINSION L J W,HENSTOCK T J,DIX J K,et al.Estimating quality factor and mean grain size of sedimnets from high resol-ution marine seismic data[J].Geophysics,2008 73(4)：19-28.

[17]吴琳．品质因子求取与补偿方法研究[D]．北京:中国石油大学,2011.

WU L.The study on methods of qualityfactor extraction and compensation for the attenuation based on it[D].Beijing:China University of Petroleum,2011.(In Chinese)

The influence factors of the spectral ratio method and its application effect analysis

WU Nan-kea,ZHOU Huai-laia,b,c

(Chengdu University of Technology a.College of Geophysics, b.State Key Laboratory of Oil and Gas Reservoir Geology and Exploitation, c.Key Lab of Earth Exploration &Information Techniques of Ministry of Education，Chengdu610059，China)

Abstract:Stratigraphic absorption and attenuation is a big problem for high resolution seismic exploration.The quality factor Q is one of the most important parameters to describe the elastic properties of rocks,and it also an important symbol of oil-bearing formation.Spectral ratio method is the most widely used method for Q estimation.This paper describes the basic principle of spectral ratio method.Using Ricker wave as seismic wavelet,and combined with the least square principle to calculate the quality factor Q from the geological model.And analyzed the layer thickness,noise,time window length,frequency band and other factors on the application effect of the spectral ratio method.Multilayer model analysis combined with seismic data of hydrocarbon detection proved that spectral ratio method can effectively estimate Q.Therefore,the spectral ratio method can be used as an effective hydrocarbon detection factor.

Key words:quality factor;spectral ratio method;influence factors

收稿日期：2015-08-05改回日期：2015-09-07

基金项目:国家自然科学基金(41204091)

作者简介：巫南克(1991-)，男，硕士，研究方向为衰减属性油气检测，E-mail：wunanke_cdut@163.com。

文章编号：1001-1749(2016)02-0225-07

中图分类号：P 631.4

文献标志码：A

DOI：10.3969/j.issn.1001-1749.2016.02.13