“认识负数”教学实录
◇张齐华
“认识负数”教学实录
◇张齐华

一 分享:我找到的负数
师:课前,同学们都收集了一些负数,并初步了解这些负数的含义。把收集的这些负数和你们的初步认识,在小组里交流一下。
(学生交流,教师倾听学生的发言,收集有价值的信息,以备随后的教学)
师:谁来说一说,你在哪里找到了负数?它们大概表示什么意思?
生:我在电梯里找到了-1层,它表示比地面还要低1层。
生:我在天气预报里找到了-2℃,它表示天气很冷。
生:我在银行卡里找到了-200元,它表示支出了200元。
生:我不同意他的想法,我觉得-200元表示欠银行 200元。
师:其实,你们说的两种意思都对,在不同的情境中,-200表示的意思的确有所不同。
生:我还在体温计上找到了负数。(生笑)是温度计上,我找到了-5℃。
师:体温计上如果出现了负数,那就太可怕了。不过,温度计上真的会出现-5这个数吗?一会儿,我们深入研究。
生:我还在海拔高度上看到负数,比如某些地方海拔很低,有-100米。
生:我还在冰箱上见过负数,我家冰箱最低温度是-18℃。
师:看来,负数在我们的生活中的确随处可见。接下来,我们将围绕这些负数,进行深入研究。
二 对话:我认识的负数
师:课前,同学们已经结合自己对负数的理解,把“-2层”“-5℃”“-155米”表示的含义,用三幅图画了出来。下面,先在组内进行交流,然后我们全班进行展示。
(学生组内交流,随后全班反馈)
生:这是我画的-2层(出示图1)。这是1层,它的下面是-1层,再往下就是-2层了。
师:对于他的作品,大家还有什么需要补充的吗?
生:我觉得还要把地面画出来,这样看起来更清楚(出示图2)。

图1
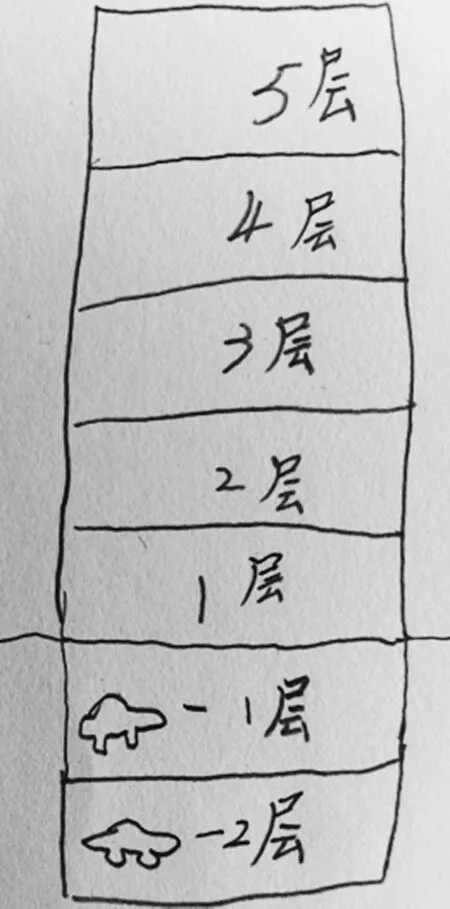
图2
生:我也觉得应该把地面画出来。只有知道地面在哪里,我们才能知道,哪些房间在地上,哪些房间在地下。地上的用正数表示,地下的用负数表示。
师:说得真好!老师这儿也画了一幅图,那是一幢有地下室的房子,现在,你能看出打问号的那层是第几层吗(出示图3)?
生:不知道。因为我们还不知道地面在哪里。
师:如果我用一条直线表示地面(出示图4),现在,你能确定问号所在的是第几层吗?

图3

图4
生:是-2层、1层、-3层、-1层。
师:奇怪,同样是这层楼,为什么大家给出的答案不一样啊?
生:因为地面变了,相应的楼层也就变了。
生:我觉得地面就像是地上和地下的分界线,分界线变了,楼层当然就变了。
生:我觉得地面就像是0层,只有我们知道0层在哪里,我们才能确定问号所在的到底是第几层。
师:说得太棒了!看来,判断楼层究竟是正数还是负数,究竟是第几层,关键还取决于地面,也就是0所在的位置啊!继续来看-5℃。谁来给大家展示一下?
生:我画了一个温度计,这个地方就是-5℃(出示图5)。
生:我觉得他画得不好,因为他没有画出0℃在哪里。就像刚才那样,如果地面不确定,楼层就没法确定。我画的图是这样的(如图6),这里是0℃,这里比0℃低5℃,所以是-5℃。
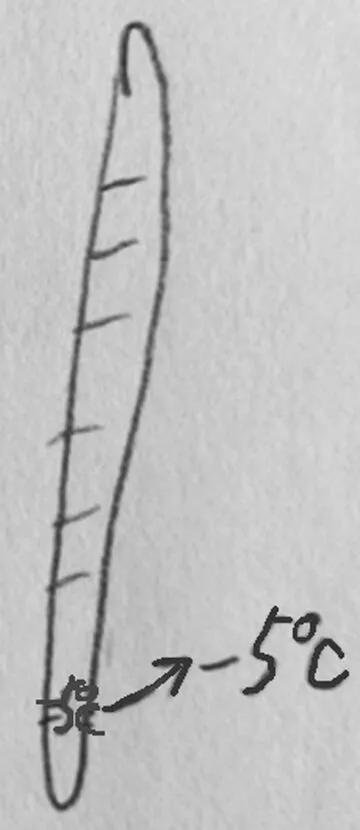
图5

图6
师:我很好奇,别的同学在0℃下面,标的都是-1、-2这样的数,你标的却是1、2、3这样的数,你是不是漏写了什么?
生:哦,我漏写了前面的减号,最后一个我补上了。
生:我觉得没漏写。我昨天观察过家里的温度计,它不管在0的上面还是下面,都没有那个减号。
师:(相机出示图7)首先,更正一下,数学上,负数前面的符号我们不叫减号,而叫负号。另外,生活中有些温度计,0下面的温度的确是没有负号的。那么问题来了,0的上面和下面都没有负号,我们到底该怎么区分哪些是正数,哪些是负数呢?

图7
生:我觉得 0上面的是正数,0下面的是负数。
生:我知道,这些液体是热胀冷缩的。温度越高,升得就越高。所以,我也认为0上面的是正数,下面的是负数。
师:真了不起!还有别的表示方法吗?
生:我画的是电视机上的新闻(出示图8)。我想告诉大家,-5℃很冷,请大家多穿点衣服。

图8
师:谢谢你的提醒,-5℃的确比较冷。课前,大家都搜集了温度中的负数,谁愿意和大家说说,你又搜集到哪个温度,感觉怎么样?
生:我收集到的是-2℃,它也比较冷,但没有-5℃冷。
生:我收集到的是-10℃,它比-5℃更冷。
生:我收集到的是-89.2℃,这是地球表面最冷的温度,在南极洲。
师:多宽的知识面啊!掌声鼓励!老师这儿也画了一个温度计(出示图9),你能从这幅图中一眼看出括号里该填什么数吗?
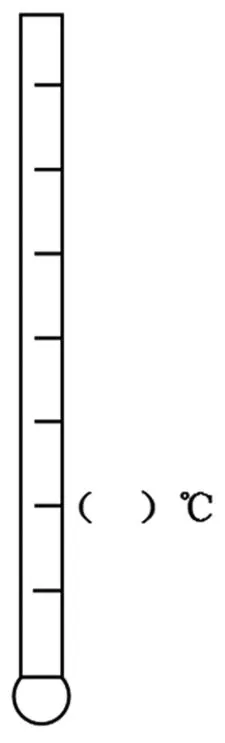
图9
生:不能,因为我们不知道0℃在哪里。
师:(在括号上方第 3根刻度线上标上“0℃”)现在,你能知道括号里该填几了吗?
生:填-3。这是0℃,它下面分别是-1℃、-2℃、-3℃。
师:(又在括号上方第 2根刻度线上标上“-5℃”)现在,你还觉得它还是-3℃吗?为什么?
生:不是-3℃了,应该是-15℃了。
师:奇怪,怎么变得那么快?
生:老师,你骗我们!原来我们以为,1格就是1℃,现在,1格代表5℃了,它在0℃以下3格,所以,当然是-15℃了。
师:小小的错误,让你体会到什么?
生:我觉得既要看清0℃在哪里,还要看清1格表示多少度,只有这样,我们才能准确说出温度计上的温度。
师:(出示图10)这是-15℃,那另两个箭头所指的温度又分别是多少?能看清的,就直接说答案;不能看清的,大概地估一估。

图10
生:我觉得上面的箭头指的是9℃。因为我们知道1格代表5℃,上面的这个温度比0℃高出差不多2格,所以我觉得它应该是9℃。
生:我觉得下面的温度应该是-18℃。这是-15℃,这是-20℃,它在-15℃和-20℃中间偏下面一点点,所以我觉得应该是-18℃。
师:看得出来,大家不仅对负数理解得很透彻,而且数感也非常好。吐鲁番盆地的海拔高度是-155米,这个负数,你们又是如何用图来表示的?
生:我画了一条线表示地面,然后从地面往下钻-155米,就可以了。(如图11)

图11
生:我反对,不应该往下钻-155米,而是往下钻155米。不然,就钻到天上去了。
生:我也画了一条线表示地面(出示图12),地面可以用 0米来表示。比它高1米的地方,就是1米;比它低的,就是-1米、-2米,直到-155米。
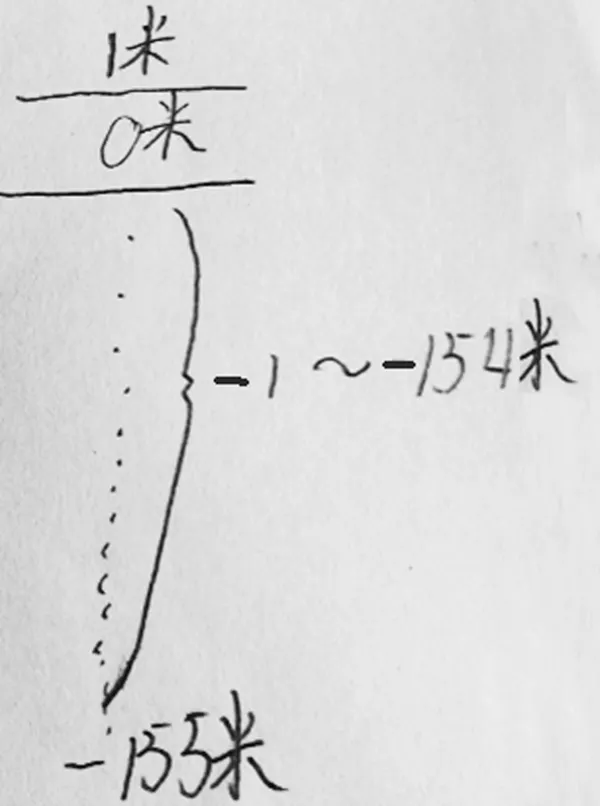
图12
生:看了这幅图,我觉得-155米其实就表示比地面低155米。
生:我觉得你们说得都不对。因为题目说了,吐鲁番盆地的海拔高度是-155米,既然是海拔高度,应该是比海平面低,而不是比地面低(出示图13)。 所以,我觉得海拔高度-155米表示的是比海平面低155米。

图13
师:说得真是太好了!的确,海拔高度,通常是以海平面的平均高度作为基准线的。比它低的,海拔高度都是负数;比它高的,海拔高度都是正数。现在,你觉得吐鲁番盆地怎么样?
生:我发现它特别低,不仅比一般的地面低,它甚至比海平面还要低。
生:如果吐鲁番盆地就在海边的话,那它就不是盆地,而是成为一个湖了。
师:(指图12)如果我们就以这幅图为例,下面的几个海拔高度,大约又在哪里?先读一读,再指一指。
(教师出示-200米、20米、155米三个海拔高度,学生先估测,再指出它们的大致位置,略)
三 沟通:我理解的负数
师:黑板上现在有3个负数(即-2,-5,-155)。如果让你写3个比它们都要小的负数,再写3个比它们都要大的负数,行吗?
(学生尝试写出了-200、-500、 -1000以及-1、-0.5、
师:看来,负数的家庭里除了负整数,还可以有负小数、负分数。在这些负数中,你认为谁最大,谁最小,你发现了什么。
生:我发现,把负号去掉后,剩下的数越小,这个数就越大;剩下的数越大,这个数就越小。
生:我还发现,负数比大小的方法和正数正好相反,数字越大,这个数反而越小。
生:我觉得没有最大的负数,也没有最小的负数。
师:观察这些负数,比较一下,你有没有发现,负数有什么共同的地方?
生:它们都有负号。
生:它们都比0小。
师:比0小的数,都是负数。负数中的负号可以省略吗?为什么?
生:不能省!如果省略,负数就都变成正数了。
师:你能上讲台来,让这些负数都变为正数吗?(学生擦掉负数前面的负号,保留两个负数)最后两个,如果不擦掉负号,你还有办法使它们变成正数吗?
(学生尝试,老师引导学生添上一竖,成为含有正号的正数)
师:想一想,负数中的负号不能省略,那正数中的正号能省略吗?为什么?
生:我觉得正号可以省略,你看前面几个正数,不都是没有正号吗?
生:我也觉得正号可以省略,因为省略完,它还是比0大,这个事实改变不了。
师:说得真好!负号不能省略,但正号可以省略。不过,有时为了和负数形成对比,我们会保留正数前面的正号。负数也研究过了,正数也研究过了,还剩下谁没有研究了?
生:0。
师:有什么问题想和大家沟通一下吗?
生:0到底是负数还是正数?
师:谁来解释一下?
生:我觉得0是正数,因为它不比0小。
生:我也觉得0是正数,因为它前面可以加上正号,加上正号后,还是0。
生:我反对。我觉得0既不是正数,也不是负数,它是正数和负数的分界点。
生:我也反对!因为负数都比 0小,正数都比0大。0既不比0大,也不比0小,它既不是正数,也不是负数。
(教师相机出示数轴,引导学生体会0的右边是正数,0的左边是负数,0是正数和负数的分界点)
师:由于负数的出现,数的大家庭又增添了一个庞大的团队,而我们的数轴也从原来的射线变成了一条直线。当然,这还远不是终点,随着学习的不断深入,数的家族还会增添更多新成员,让我们共同期待吧!
(作者单位:江苏南京市北京东路小学)

