双腔液固混合介质隔振器刚度阻尼特性分析

李方硕， 陈　前， 周俊辉

(南京航空航天大学 机械结构力学及控制国家重点实验室, 南京　210016)

双腔液固混合介质隔振器刚度阻尼特性分析

李方硕， 陈前， 周俊辉

(南京航空航天大学 机械结构力学及控制国家重点实验室, 南京210016)

摘要：双腔液固混合介质隔振器由波纹管式液固混合介质隔振器和附加腔室通过管道联通构成。建立了联通管道内部液柱的运动方程，推导了隔振器非线性动力学模型。为分析隔振器刚度和阻尼特性，将平方阻尼简化成线性阻尼，得到了简谐激励下隔振系统线性简化模型，并求得了隔振系统刚度和损耗因子的表达式。分析了阀门节流开度、振动幅值、激励频率、主腔室刚度对于系统刚度和损耗因子的影响。结果表明，虽然隔振系统刚度和损耗因子受多种因素影响，但是二者上下限只由两个腔室的等效刚度决定。为检验理论模型，进行了动态特性试验，试验结果和理论结果基本一致，证明了动力学模型的可靠性，试验结果还表明液柱共振会造成刚度特性曲线出现峰值，恶化系统的隔振特性。

关键词：液固混合介质；隔振；双腔；波纹管

低频重载动力机械隔振是隔振工程中的重点和难点，对于航空结构和舰船隔振具有重要研究意义[1-2]。低频重载隔振要求隔振系统必须同时具有承载能力大和刚度低两种特性，传统的机械弹簧可以通过预压缩的方法提高承载能力，但是由于弹簧长度和压缩量的限制，往往无法同时满足承载和刚度要求；空气弹簧具有较好的承载和刚度特性，但在维护性、可靠性和使用寿命等方面需要进一步的改进[3]。

液固混合介质隔振器是一类适用于低频重载隔振的新式隔振器[4]，它主要由压力容器、传力液体和弹性单元体构成。液固混合介质的概念最早由Wo等[5-6]提出，Gao等[7-8]首先将其用于低频重载隔振领域，先后设计了活塞油缸式、波纹管式两种压力容器，并对实心橡胶球、空心橡胶球、波纹管单元体、沸石几种固体介质力学特性进行了研究，取得了一系列的研究成果。

液固混合介质隔振器可以通过选择弹性单元体材质和配置弹性单元体数量获得良好的刚度特性，但由于隔振器安装体积的限制，单个压力容器有时无法满足单元体装填需求。为了进一步改善隔振系统刚度和阻尼特性，本文提出了带附加腔室的波纹管液固混合介质隔振器的设计概念[9-10]。文章介绍了双腔隔振系统的结构模型，运用液压流体力学建立了联通管道内部液柱动量方程，基于能量等效，将流体阻尼简化为线性黏性阻尼处理，从而得到隔振器等效刚度表达式，最后通过数值和试验分析了隔振器等效刚度各种影响因素。双腔隔振器可以直接用于被动隔振，也可以通过调节阀门开度实现变刚度半主动控制，本文研究介绍了隔振器主要力学特性，有助于进一步改善隔振器设计。

1隔振器动力学模型

1.1隔振器结构

隔振器的模型如图1所示，主要由主腔室(main chamber，多层波纹管容器)、附加腔室(additional chamber，刚性容器)、联通管道、节流阀和若干波纹管弹性单元体组成。波纹管容器作为弹性结构，既是压力容器又是承力构件，当主腔受到压缩时，波纹管容器和单元体受力变形，产生弹性回复力。附加腔室是刚性结构，内部充满油液和弹性单元体组成的液固混合介质。通过改变节流阀开度可以限制附加腔室的作用，阀门全关时，附加腔室不起作用，全开时两个腔室完全连通。

图1　双腔液固混合介质隔振器Fig.1 The dual-chamber liquid and solid mixture vibration isolator

1.2隔振器力学模型

图2为隔振系统的力学模型示意图。k0为主腔室波纹管容器结构的等效刚度，Ap为波纹管容器平均截面积， m代表主腔室内所有弹性单元体组成的子系统， a代表附加腔室内所有弹性单元体组成的子系统。Pm为主腔油压，Pa为附加腔室油压，q为油液流经管道的体积流量，kn、ka为子系统内部油压对于子系统体积的导数，单位为Pa/m5。波纹管单元体结构阻尼较小，可以忽略不计，因此只需要考虑m子系统和a子系统弹性变形特性。

图2　隔振器力学模型Fig.2 Mechanical model of the vibration isolator

x1=pa·(kaAp)-1

x=pm·(kmAm)-1+x1

假设隔振器在静平衡处额外受到动载荷F作用，则隔振器的动力学方程为

F=k1(x-x1)+k0x

(1)

根据非定常伯努利方程可得联通管道内油液运动的振动方程

(2)

式(1)、(2)构成了隔振系统的非线性动力学模型，其中c1为油液流经管道产生的摩擦阻尼，c2为阀门节流产生的小孔阻尼，meq为液柱振动的等效质量，它们分别可以表示为

(3)

(4)

式中，At为管道截面积，lt为管道长度，μ为油液的动力黏度，Av为节流阀流通面积，ρ为油液密度，Cd为流量系数，当d1≥7d2时，Cd在(0.61,0.62)间取值，否则在(0.7,0.8)间取值。由于压差流量模型存在误差，meq和c2有时需要通过修正因子修正。令mr为液柱实际质量，mr=ltAtρ，结合式(4)，有

由于通常Ap>At，可知振动过程中，液柱影响被放大了。

2简化系统刚度模型

(5)

式(5)中,a1为x1的振动幅值,ω为激励频率，此时隔振器力学模型简化为

(6)

引入隔振系统的等效刚度keq和等效损耗因子ηeq则隔振系统复刚度可以表示为

kcom=(1+jηeq)keq

(7)

对式(6)进行傅里叶变换可以得到线性简化系统刚度和损耗因子表达式

(8)

(9)

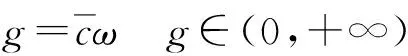
(10)

由式(8)可知，当激励频率满足meqω2>k1+k2时，总有keq>k1+k2时，此时附加腔室的存在不仅没有进一步改善系统的刚度特性，还恶化了系统高频隔振性能。在实际应用过程中，为避免高频段出现刚度硬化现象，工作频率应满足meqω2≪k1+k2时，此时式(8)、(9)可以近似表示为

(11)

由式(11)、(12)可知，随着g增大，刚度keq单调增大，损耗因子ηeq先增大后减小。进一步分析两式，可知等效刚度和等效损耗因子均有上下限：keq∈(kmin,kmax)，ηeq∈(0,ηmax)，边界值分别为

(13)

(14)

将g写成函数形式，g=g(ω,a1,Av)，由式(5)、(10)可知，增大激励频率、振动幅值，减小阀门节流面积都会引起系统刚度的增大。结合图2和式(6)可知，kmin对应阻尼力和惯性力为零的情况，kmax对应节流阀闭合，只有主腔室作用的情况。

液固混合介质隔振器突出优点是具有刚度可调性，可以通过改变单元体数量或者改变单元体材质设定特定的刚度值，因此有必要研究刚度参数变化对于双腔隔振系统力学特性的影响。下面将对式(6)进行仿真分析，研究主腔等效刚度k1对于损耗因子ηeq的影响。仿真参数如下:k0=1.8×105N/m,k1∈(105,109) N/m,k2=2.4×105N/m,meq=100 kg，c1=0，dv为节流阀流通截面等效直径，且dv=8 mm。对于式(6)施加位移激励,x=acosωt,a=0.1 mm,仿真结果见图3。

图3　主腔刚度对于损耗因子的影响Fig.3 Effect of the main chamber equivalent stiffness on loss factor

图3中曲线上标注数字为主腔刚度k1的值，单位为N/m，从图中可以看出，损耗因子随着主腔刚度增大而增大。实际上，当主腔失去弹性时，液固双腔隔振系统变为一个油液阻尼缓冲系统[11]，可以取得最佳的阻尼效果；当主腔刚度较小时，隔振系统将类似一个双腔空气弹簧[10]，具有低刚度低阻尼特性。另外由于损耗因子具有单一峰值，通过合理调整两个腔室刚度参数，可以使隔振器在共振时取得最佳的能量耗散效果，从而有效抑制共振峰值。双腔液固混合介质隔振器的一个关键问题即是设计主腔、附加腔室刚度参数，使隔振器在给定工况下取得最佳的隔振缓冲效果。另外从图3可以看出，在高频段，损耗因子随着激励频率升高递减，这有助于改善系统高频段的隔振特性。

3试验研究

图4　隔振器力学特性试验Fig.4 The experiment of the vibration isolation system

为检验理论模型，利用疲劳试验机对于隔振器进行力学特性试验。试验装置见图4，疲劳试验机上的构件为主腔室波纹管容器，左侧的附加腔室为轴向约束的波纹管容器，代替刚性压力容器，二者通过高压油管和球阀相连，两个腔室内部装满油液和弹性单元体组成的液固混合介质。其中各刚度参数约为：k1=1.36×106N/m,k2=2.4×105N/m,k0=1.8×105N/m。准静态加载速度为每分钟1 mm；动态加载预压缩2 mm，施加幅值为0.1 mm、0.2 mm正弦激励。

图5～6为双腔隔振系统准静态压缩特性曲线，可以看出，隔振器刚度近似为线性。图5为阀门开启的情况，准静态刚度约为,kopen=3.6×105N/m，图6为阀门关闭的情况，准静态刚度约为kclose=1.36×106N/m。当不考虑管道内部液柱振动，并假设波纹管容器静态刚度和动态刚度相同时，有kopen=kmin，kclose=kmax。

图7～12为阀门全开、半开、闭合三种情况下隔振器刚度和损耗因子变化特性曲线。其中图7～10中experimental 对应试验结果，numerical对应基于非线性动力学模型的数值仿真结果，model对应于基于线性简化系统刚度损耗因子模型的仿真结果。对比试验和仿真结果，可以看出，理论结果和试验结果有着很好的一致性，从而验证了理论模型的合理性。

图7为全开情况，可见随着激励频率的增大，刚度先增大后减小。9.5 Hz附近的峰值点是由联通管道内部液柱共振引起的，通过式(2)可以计算液柱的共振角频率

(15)

液柱共振可以引起系统刚度升高，恶化隔振性能，由式(4)、(15)可知，处理液柱共振可以通过两个手段：一是通过缩短管道长度lt和增大联通管道截面积At减小液柱等效质量meq，理想的情况下两个腔室通过节流孔连接，此时可以忽略液柱等效质量；二是增大主腔刚度k1，极限的情况是，主腔完全刚性，则在有限频带内，液柱不会产生共振。当液柱共振频带位于隔振频带以外时，可以忽略液柱的负面影响。

图9为阀门半开情况，此时由于阀门开度较小，平方阻尼系数较大，有效的抑制了液柱共振，因此刚度随频率升高单调递增，没有共振峰值。从图8和图10可以看出，液柱共振不会影响损耗因子的变化趋势，当簧载系统共振频率和损耗因子峰值频率一致时，隔振系统可以有效的抑制共振峰值。

图5 阀门开启时准静态试验Fig.5Thequasi-staticexperimentwhenthevalveisopen图6 阀门闭合时准静态试验Fig.6Thequasi-staticexperimentwhenthevalveisclosed图7 阀门全开时刚度变化特性曲线Fig.7Theequivalentstiffnesswhenthevalveisfullyopen

图8 阀门全开时损耗因子变化特性曲线Fig.8Theequivalentlossfactorwhenthevalveisfullyopen图9 阀门半开时刚度变化特性曲线Fig.9Theequivalentstiffnesswhenthevalveissemi-open图10 阀门半开时损耗因子变化特性曲线Fig.10Theequivalentlossfactorwhenthevalveissemi-open

图11～12为阀门关闭情况下的理论和试验结果，试验激励幅值分别为0.1 mm和0.2 mm。阀门关闭时，系统的理论刚度为恒值，可以通过图6所示准静态试验获得；由于在建模过程中忽略了波纹管金属结构阻尼和油液振动产生耗散作用，因此在阀门全闭时，损耗因子理论值为零。从图11～12可以看出，系统等效刚度在1.36×106N/m上下波动，而损耗因子较小，可见此时系统阻尼可以忽略不计，试验结果验证了刚度阻尼假设的合理性。图11～12中曲线不够光滑，原因是疲劳试验机在动态加载时存在测量误差。

图11　阀门全闭时刚度试验曲线Fig.11 The equivalent stiffness when the valve is closed

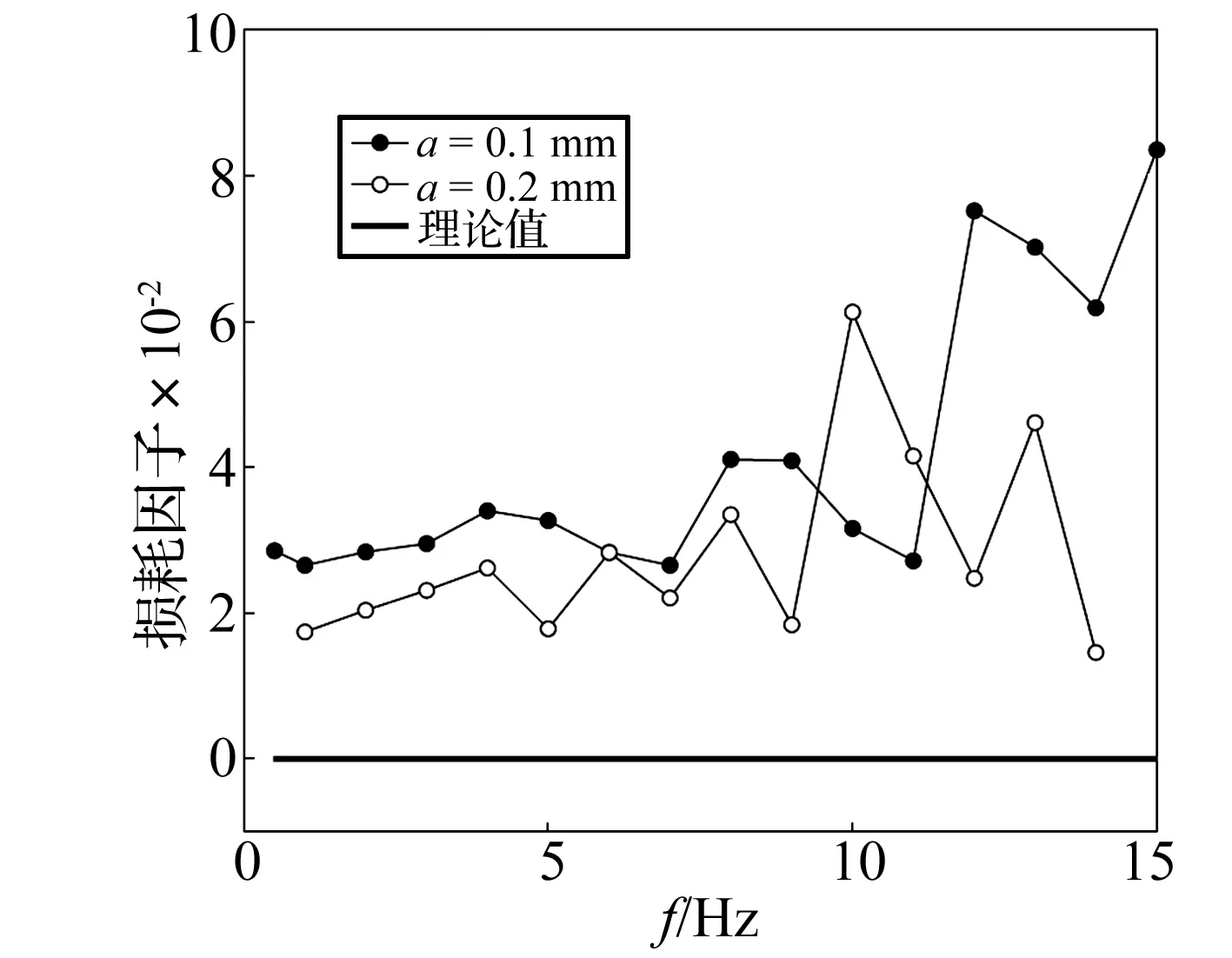
图12　阀门全闭时损耗因子试验曲线Fig.12 The equivalent loss factor when the valve is closed

4结论

本文建立了双腔液固混合介质隔振系统非线性动力学模型，推导了系统线性简化模型下刚度和损耗因子的表达式。试验和仿真结果表明：

(1) 在不考虑液柱作用情况下，增大阻尼系数和激励频率将会增大隔振器的等效刚度。

(2) 可以通过调节两个腔室的刚度参数调节系统的刚度阻尼特性。

(3) 液柱共振会引起刚度峰值，恶化系统刚度特性。

本文的研究有助于双腔液固混合介质隔振器改进设计，并为下一步的变刚度设计提供理论基础。接下来的研究集中在三点:① 是进一步研究管道液柱振动对于隔振系统的影响，并设法避免液柱共振；② 是优化两个腔室刚度参数，以获得最佳的刚度阻尼特性；③ 是研究隔振器承载情况下动力学特性和隔振特性。

参 考 文 献

[1] 何琳. 潜艇声隐身技术进展[J]. 舰船科学技术, 2006, 28(增刊2): 9-17.HE Lin.Development of submarine acoustic stealth technology [J]. Ship Science and Technology,2006, 28(Sup2): 9-17.[2] 聂宏，魏小辉. 大型民用飞机起落架关键技术[J]. 南京航空航天大学学报, 2008, 40(4): 427-432.

NIE Hong, WEI Xiao-hui. Key technologies for landing gear of large civil aircrafts[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2008, 40(4): 427-432.

[3] 张利国，张嘉钟，贾力萍，等. 空气弹簧的现状及其发展[J]. 振动与冲击, 2007, 26(2): 146-151.

ZHANG Li-guo, ZHANG Jia-zhong, JIA Li-ping, et al. Future and development of air springs[J]. Journal of Vibration and Shock, 2007, 26(2): 146-151.

[4] Teng H D, Chen Q. Study on vibration isolation properties of solid and liquid mixture[J]. Journal of Sound and Vibration, 2009, 326(1/2): 137-149.

[5] Wa C. Preliminay investigation into mechanical properties and potential applications of a novel shock absorbing liquid[D]. Manchester UK: The University of Manchester, 1999.

[6] Wa C, So O. Preliminary investigation into the mechanical properties of a novel shock absorbing elastomeric composite[J]. Journal of Materials Processing Technology, 2001, 119: 379-386.

[7] Gao Xue, Chen Qian, Teng Han-dong. Modeling and dynamic properties of a novel solid and liquid mixture vibration isolator[J]. Journal of Sound and Vibration, 2012, 331(16): 3695-3709.

[8] 余慕春，陈前，高雪，等. 分子弹簧的隔振机理与力学性能研究[J]. 力学学报, 2014,46(4): 553-560.

YU Mu-chun, CHEN Qian, GAO Xue, et al. Investigation of molecular spring on vibrations isolation mechanism and mechanical properties[J]. Chinese Journal of Theoretical and Applied Mechanics, 2014,46(4): 553-560.

[9] Lee J, Kim K. A method of transmissibility design for dual-chamber pneumatic vibration isolator[J]. Journal of Sound and Vibration,2009, 323(1/2): 67-92.

[10] Lee J, Kim K. Modeling of nonlinear complex stiffness of dual-chamber pneumatic spring for precision vibration isolations[J]. Journal of Sound and Vibration,2007, 301(3/4/5): 909-926.

[11] 顾宏斌，刘晖，吴东苏. 现代起落架缓冲系统的发展[J]. 航空科学技术, 2008(2): 36-41.

GU Hong-bin, LIU Hui, WU Dong-su. Development of research on modern landing gear shock absorber[J]. Aeronautical Science and Technology, 2008(2): 36-41.

Stiffness and damping properties of dual-chamber liquid and solid mixture vibration isolator

LI Fang-Shuo, CHEN Qian, ZHOU Jun-hui

(State Key Laboratory of Mechanics and Control of Mechanical Structures,Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China)

Abstract:The Bellows type Solid and Liquid Mixture (B-SALiM) vibration isolator, mainly proposed for vibration isolation of heavy machines with low natural frequency is formed with a multi-layer bellow container filled with SALiM working media including elastic elements and incompressible liquid. The dual-chamber SALiM vibration isolator is a B-SALiM vibration isolator linked with an incompressible pressure vessel by a tube and a valve. Based on the knowledge of fluid mechanics and dynamics, the nonlinear dynamics model of a novel vibration isolation system was established. To simplify the analysis of the stiffness and damping, a corresponding linear dynamics model and a complex stiffness were derived by simplifying the fluid damping into linear viscous damping when the isolator is excited by sinusoidal signal. A numerical simulation and an experiment were done to analyze the properties of the stiffness and loss factor. The results show that the stiffness and loss factor of the dual-chamber SALiM vibration isolator are affected by many factors such as the valve aperture/the main chamber stiffness/the exciting frequency/the vibration level and so on. The reliability of the nonlinear dynamic model was verified experimentally and the test results were generally consistent with the theoretical. It also can be illustrated from the experimental results that the oil vibration in the tube could cause bad effects on the vibration isolation effectiveness.

Key words:solid-liquid mixture; vibration isolation; dual-chamber; bellows

基金项目：江苏高校优势学科建设工程资助项目；中央高校基本科研业务费专项资金资助项目；江苏省普通高校研究生科研创新计划资助项目(KYLX_0235)

收稿日期：2015-04-14修改稿收到日期：2015-05-25

通信作者陈前 男，博士，教授，博士生导师，1951年11月生

中图分类号:TH113.1

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.10.014

第一作者 李方硕 男，博士生，1989年8月生