净信号的局部建模算法及其在近红外光谱分析中的应用

张红光，卢建刚

浙江大学工业控制技术国家重点实验室，浙江 杭州 310027

净信号的局部建模算法及其在近红外光谱分析中的应用

张红光，卢建刚*

浙江大学工业控制技术国家重点实验室，浙江 杭州 310027

提出了一种基于净信号分析的局部建模算法，以克服光谱定量分析中样本间差异性过大和样本待测性质与光谱之间存在非线性等问题。首先利用净信号分析方法得到校正样本和待测样本的净信号，然后用待测样本净信号和校正样本净信号之间的欧式距离作为样本相似性判据，选取一定数量的与待测样本最相似的校正样本组成局部校正子集，建立局部PLS回归模型。针对一组猪肉近红外光谱数据集的实验结果表明，该方法的预测精度显著优于全局建模方法和基于光谱欧式距离的局部建模方法。

光谱定量分析； 局部校正方法； 净信号； 偏最小二乘； 近红外光谱

引 言

近红外光谱分析技术发展很快，已经被广泛应用于食品、农业、医药、石化等领域[1-5]，这主要是因为其具有快速、无损、无需或只需少量样本预处理等优点。然而，近红外光谱往往存在背景漂移，噪声干扰严重，谱带重叠以及信号弱等问题[6]，无法直接从光谱获取有用信息，必须依赖多元数据分析。从而，多元数据分析一直是近红外光谱分析中的研究热点。目前，常用的多元数据分析方法有多元线性回归(MLR)[7]、主成分回归(PCR)[8]、偏最小二乘(PLS)[9]、人工神经网络(ANN)和支持向量机(SVR)[10]。其中，PLS是应用最广泛的一种方法。作为一种线性方法，PLS通过建立光谱响应与待测性质之间的线性模型进行定量分析。但近红外光谱响应与物性之间往往会存在非线性，此时，PLS模型的精度就不是很理想。此外，因校正样本数目过多和校正样本性质值分布较广而引起样本间差异显著，也会使PLS模型的精度下降。为了克服以上问题，一些非线性方法，包括ANN、SVM和高斯过程回归(GPR)[11[12-14]。

局部建模方法的关键在于选取合适的相似判据，根据相似判据选取与待测样本相似的校正样本组成局部校正子集，建立局部回归模型。通常采用样本光谱间的欧式距离作为相似判据[12]，样本光谱间欧式距离越小，样本相似度越高。然而，由于近红外光谱往往包含噪声，背景等与性质无关的信息，在很多情况下样本光谱间的欧式距离并不能真实体现样本间的相似度，这时如果采用光谱欧式距离作为样本相似判据，需要选取更多的校正样本来包含待测样本所在的性质变化区间，非线性问题无法得到很好的解决，而进一步影响基于局部校正子集建立的局部回归模型的预测精度。

为了消除近红外光谱中噪声背景等无关信息对样本相似性判断的影响，提出一种基于净信号分析[15]的局部建模算法，对样本近红外光谱进行净信号分析，得到不含噪声背景等无关信息的净信号，利用样本净信号间的欧氏距离作为样本相似性判据，选取局部校正子集并建立局部回归模型。最后通过一组公开的近红外光谱数据集验证了本方法的有效性。

1 原理与算法

1.1 净信号分析

Lorber将净信号定义为样本光谱的一部分，正交于样本光谱中其他的干扰信息[15]。目前有多种方法用于净信号的计算，本文将采用Lorber所提出的方法[16]，其计算过程如下：

1)首先对校正样本集R进行主成分分析，并利用前P个主成分进行光谱重构，得到重构光谱集RP。

2)基于RP计算出与待测成分k子空间正交的其他信息组成的子空间RP, -k，计算方式为

RP, -k=RP-αykdk

(1)

3)yk是待测组分的估计值，计算方式为

(2)

其中上标“+”表示Moore-Penrose伪逆，y是校正样本集的浓度矩阵。

4)式(1)中的α是标量，可通过式(3)计算

(3)

5)式(1)和式(3)中的dk表示的是待测组分的光谱信息，可由重构光谱集RP的平均光谱代替，通过式(1)，式(2)和式(3)，可以得到正交于RP, -k的映射矩阵

H=I-(RP, -k)+RP, -k

(4)

6)样本光谱的净信号NAS (net analyte signal)可由式(5)得到

NAS=Hr

(5)

如上所述，净信号分析方法通过获得包含所有干扰信号的子空间，然后从样本光谱中去除无用信息，得到表征样本待测组分的有效信息。由于样本的净信号已经消除了噪声背景等干扰因素，基于样本净信号间的欧式距离能更好地表征样本间的相似度。

1.2 基于净信号的局部回归模型

基于净信号的局部PLS回归模型建立流程如图1所示。首先对校正样本集进行净信号分析，得到校正样本集的净信号和净信号映射矩阵H。利用样本净信号间的欧式距离作为样本相似性判据，选取一定数目与待测样本最为相似的校正样本组成局部校正子集，建立局部回归模型，得到待测样本的预测值。

为了便于简明地比较各模型结果，将经典的全局PLS (Global PLS)记为G-PLS，将常用的基于光谱欧式距离的局部PLS(euclidean-distance local PLS) 记为EL-PLS，将工作新提出的基于样本净信号间的欧式距离的局部PLS (NAS euclidean-distance local PLS) 记为NAS-EL-PLS。

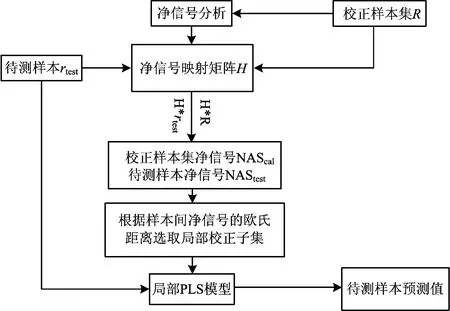
Fig.1 Procedure of local PLS model based on net analyte signal

1.3 局部PLS模型参数优化

在局部PLS模型的建立过程中，需要确定的参数包括校正子集数目Nlocal和局部模型的潜变量个数A。采用留一法交叉验证方式进行参数优化，评价指标为交叉验证均方根误差(RMSECV)。N-PLS模型参数优化具体步骤如下： 根据G-PLS模型确定最大潜变量个数Amax，然后每次取出一个校正样本，用剩下的校正样本根据式(1)—式(5)求出剩下的校正样本的净信号和留出样本的净信号，然后计算出留出样本与剩余校正样本净信号间的欧氏距离作为样本相似性判据。局部模型的潜变量个数A从1到Amax，对应每个潜变量个数A，定义一个校正子集数目的取值表： [A+1,A+2,A+5,A+10, …,Nlocal, …,N-1]，N是校正样本个数。进行留一法交叉验证，考察潜变量个数和校正子集数目对RMSECV的影响。留一法交叉验证过程中，依次留出一个校正样本，根据留出的校正样本与剩下的校正样本间相似性判据的大小，选取校正子集。最终确定使RMSECV最小的潜变量个数A和校正子集数目Nlocal。

EL-PLS模型参数优化与NAS-loc-PLS模型类似，只是采用光谱间的欧氏距离作为光谱相似性判据，在此不再赘述。

2 实验部分

2.1 样本数据集

实验所用数据为一组由一台Tecator近红外光谱仪测得的猪肉近红外光谱数据集。每条光谱包含100个波长点，范围为850～1 050 nm。该数据集由225个样本组成，并且该样本集被获取时，已经分成了一个包含172个样本的校正样本集和一个包含43个样本的测试样本集[17]。前期研究工作表明[17-18]，该数据集尤其是脂肪含量与光谱响应之间存在明显的非线性。这主要由于猪肉样本成分复杂性以及样本的脂肪含量变化范围较大(0.9～49.1 wt%)。这里选取猪肉样本的脂肪含量作为研究对象。所有程序均采用Matlab 7.1 编写，在Windows 7环境下运行。

2.2 性能评价指标

通过G-PLS，EL-PLS以及NAS-loc-PLS模型预测性能的对比，验证本方法的有效性。这里，模型预测性能由交叉验证均方根误差(RMSECV)和预测均方根误差(RMSEP)评价。

3 结果与讨论

3.1 模型参数的选取

如前文所述，NAS-loc-PLS模型需要确定的参数为校正子集数目Nlocal和局部模型的潜变量个数A。由于G-PLS的最优潜变量数为13，所以NAS-EL-PLS和EL-PLS的所能用的最大潜变量数Amax=13。基于交叉验证的方式，得到NAS-EL-PLS模型参数NL和A与RMSECV之间的关系，如图2所示。

从图2中可以得知当A=7，NL=23时，NAS-EL-PLS的RMSECV最小，达到最优性能。类似的可以得到EL-PLS的最优模型参数为：A=10，NL=41。

3.2 模型预测性能的对比

使用RMSECV作为评价指标来比较各个模型的性能。同时为了比较各模型的对未知样本的预测能力，使用各模型对测试集里的未知样本进行预测，得到各个模型的RMSEP。表1中给出了各个模型性能的对比。

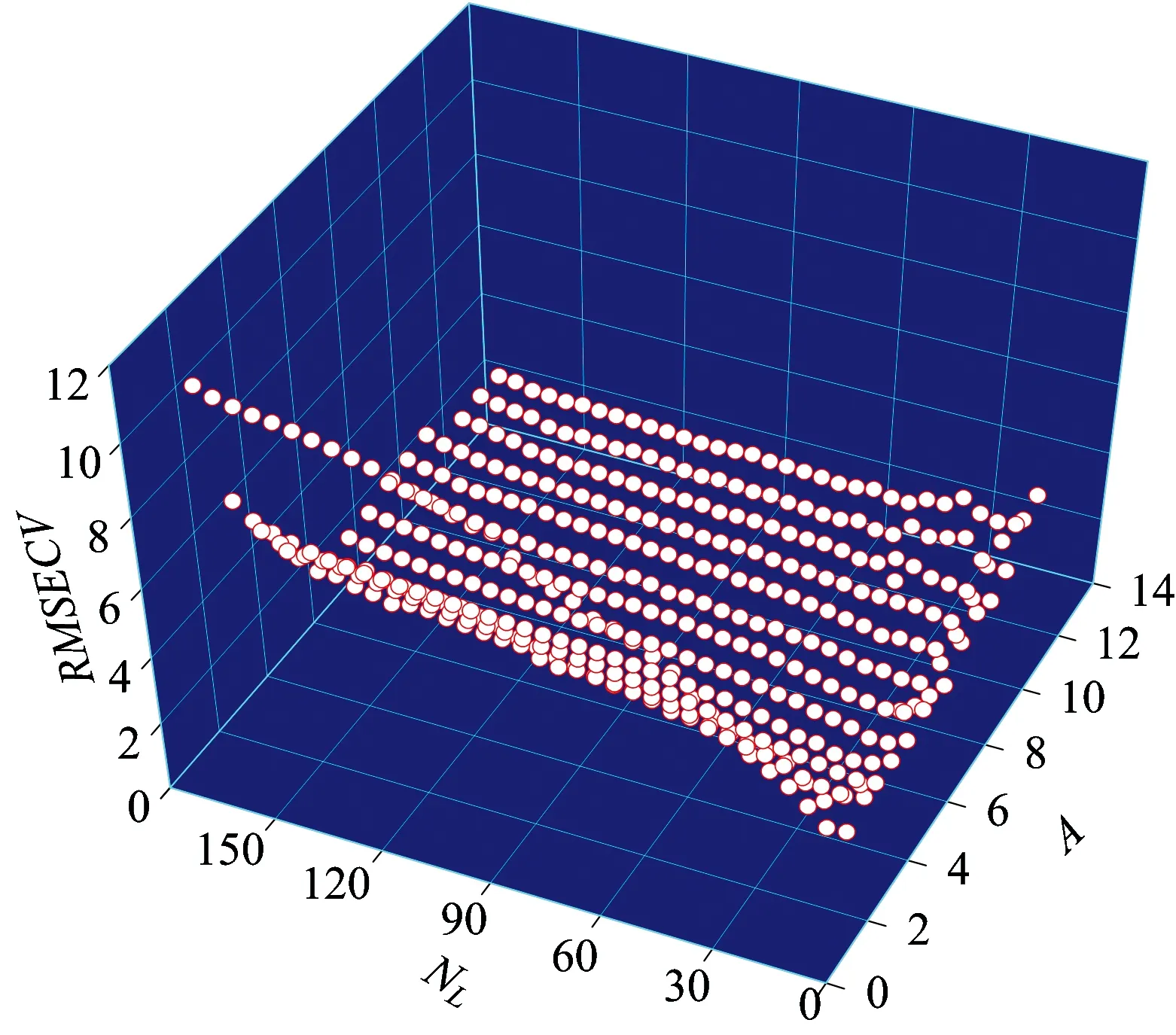
Fig.2 Influence of model parameters on RMSECV of NAS-EL-PLS model

Table 1 Comparison of performance among three models

如表1所示，两种局部模型的主因子数和所需校正样本数均显著小于全局模型，同时RMSECV也显著小于全局模型。比较三种模型对未知样本的预测性能，NAS-EL-PLS模型显著优于G-PLS和EL-PLS模型。EL-PLS模型对未知样本的预测能力最差。所以无论从模型的复杂度，以及模型的预测性能，NAS-EL-PLS模型均显著优于G-PLS和EL-PLS模型。NAS-EL-PLS模型只需选用很少的校正样本就能够获得比全局模型更好的预测性能。EL-PLS模型的预测能力很差，表明了基于样品光谱间欧式距离作为样本相似判据，有时并不能真实体现样本的相似性，因此基于光谱欧式距离的局部模型的预测性能很可能比全局模型还差。而样本净信号由于已经去除了噪声背景等无关因素的干扰，样本净信号间的欧氏距离能够更好的表征样本间的相似性。

为了进一步比较各模型的预测性能，图3给出了各模型对测试集预测时预测值与真实值的对比图。可知，G-PLS和EL-PLS模型的预测有较大的偏差，而NAS-EL-PLS模型预测性能最好，且显著优于其他模型。

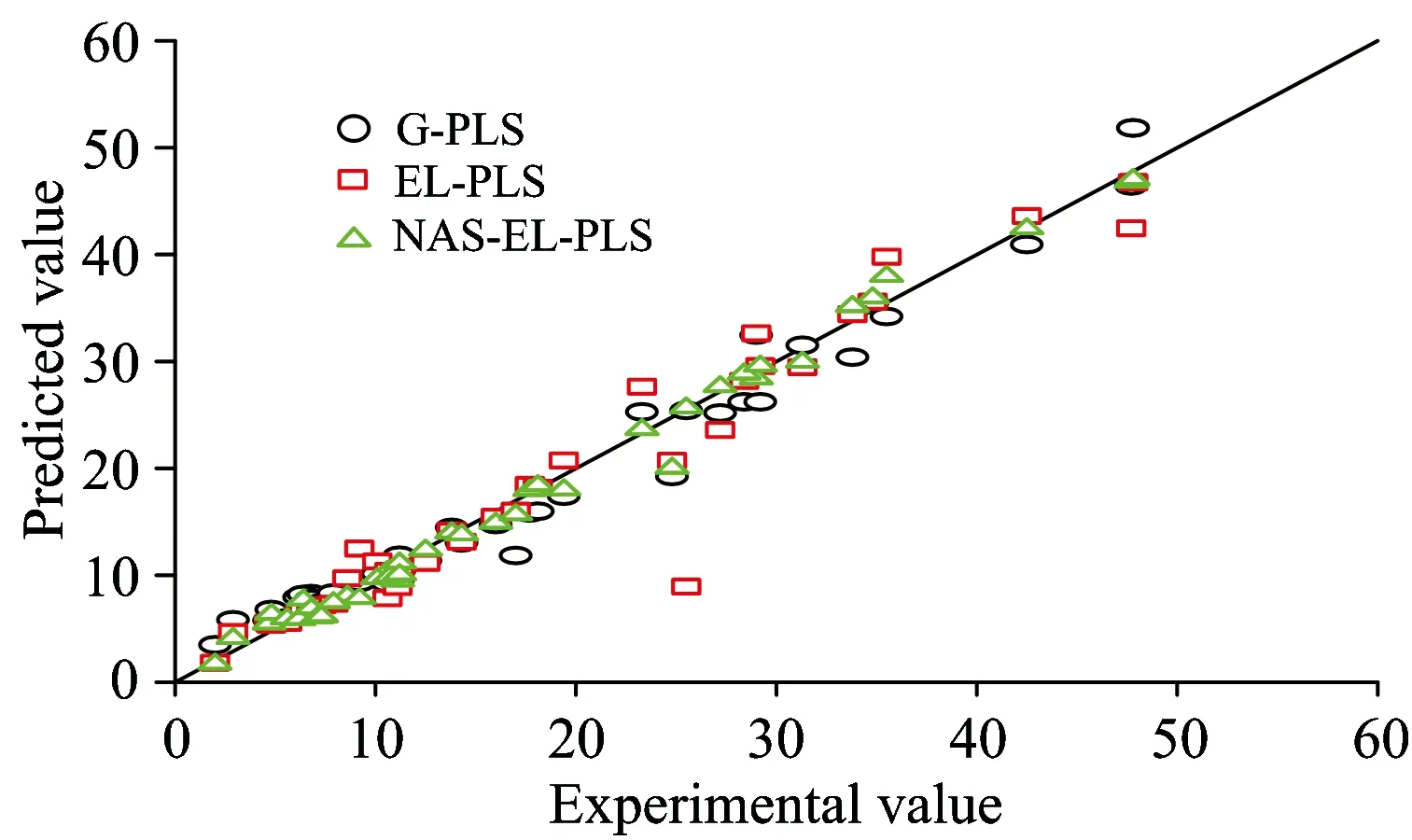
Fig.3 Comparison of models

4 结 论

提出了一种基于净信号的局部建模算法，利用净信号分析方法得到样本的净信号。通过净信号分析方法能够消除样本光谱里噪声背景等无关信息，因而以样本净信号间的欧式距离能够更好体现样本间的相似性。将该方法应用于一组公开的近红外光谱数据集，实验结果表明该方法显著优于全局偏最小二乘算法和基于光谱欧式距离的局部偏最小二乘算法。

[1] Guy F, Prache S, Thomas A, et al. Food Chemistry, 2011, 127: 1280.

[2] ZHANG Hong-guang, YANG Qin-min, LU Jian-gang, et al(张红光，杨秦敏，卢建刚，等). Spectroscopy and Spectral Analysis(光谱学与光谱分析), 2014, 34(4): 972.

[3] Roggo Y, Chalus P, Maurer L, et al. Journal of Pharmaceutical and Biomedical Analysis, 2007, 44: 683.

[4] Balabin R M, Safieva R Z. Analytica Chimica Acta, 2011, 689: 190.

[5] Zhang H G, Yang Q M, Lu J G. Spectrochimica Acta Part A: Molecular and Biomolecular Spectroscopy, 2014, 120: 625.

[6] Shao X G, Du G R, Jing M, et al. Chemometrics and Intelligent Laboratory Systems, 2012, 114: 44.

[7] Ben-Gera I, Norris K H. Journal of Food Science, 1968, 33: 64.

[8] HOU Zhen-yu, CAI Wen-sheng, SHAO Xue-guang(侯振雨，蔡文生，邵学广). Chinese Journal of Analytical Chemistry(分析化学), 2006, 34(5): 617.

[9] Chen D, Hu B, Shao X G, et al. Analytical and Bioanalytical Chemistry, 2005, 381: 795.

[10] BAO Xin, DAI Lian-kui(包 鑫，戴连奎). Chinese Journal of Analytical Chemistry(分析化学), 2008, 1: 75.

[11] Chen T, Morris J, Martin E. Chemometrics and Intelligent Laboratory Systems, 2007, 87: 59.

[12] Xie Y L, Kalivas J H. Analytica Chimica Acta, 1997, 348: 29.

[13] Center V, Massart D L. Analical Chemistry, 1998, 70: 4206.

[14] SHI Xue, CAI Wen-sheng, SHAO Xue-guang(石 雪，蔡文生，邵学广). Chinese Journal of Analytical Chemistry(分析化学), 2008, 8: 1093.

[15] Lorber A. Analytical Chemistry, 1986, 58: 1167.

[16] Lorber A, Faber K, Kowalski B R. Analytica Chimica Acta, 1997, 69: 1620.

[17] Borggaard C, Thodberg H H. Anal. Chem., 1992, 64: 545.

[18] Thodberg H H. IEEE Transactions on Neural Networks, 1996, 7: 56.

*Corresponding author

Local Regression Algorithm Based on Net Analyte Signal and Its Application in Near Infrared Spectral Analysis

ZHANG Hong-guang, LU Jian-gang*

State Key Laboratory of Industrial Control Technology, Zhejiang University, Hangzhou 310027, China

To overcome the problems of significant difference among samples and nonlinearity between the property and spectra of samples in spectral quantitative analysis, a local regression algorithm is proposed in this paper. In this algorithm, net signal analysis method(NAS) was firstly used to obtain the net analyte signal of the calibration samples and unknown samples，then the Euclidean distance between net analyte signal of the sample and net analyte signal of calibration samples was calculated and utilized as similarity index. According to the defined similarity index, the local calibration sets were individually selected for each unknown sample. Finally, a local PLS regression model was built on each local calibration sets for each unknown sample. The proposed method was applied to a set of near infrared spectra of meat samples. The results demonstrate that the prediction precision and model complexity of the proposed method are superior to global PLS regression method and conventional local regression algorithm based on spectral Euclidean distance.

Spectral quantitative analysis; Local regression; Net analyte signal; Partial least square; Near infrared spectra

Jul. 29, 2014; accepted Nov. 15, 2014)

2014-07-29，

2014-11-15

国家(973计划)项目(2012CB720500)，国家自然科学基金项目(61590925)资助

张红光，1987年生，浙江大学控制系博士研究生 e-mail： hgzhang@iipc.zju.edu.cn *通讯联系人 e-mail： jglu@iipc.zju.edu.cn

O657.3

A

10.3964/j.issn.1000-0593(2016)02-0384-04