基于判断聚合模型的推荐系统冷启动问题研究

李　莉，唐晓嘉（西南大学逻辑与智能研究中心，重庆400715）



基于判断聚合模型的推荐系统冷启动问题研究

李莉，唐晓嘉
（西南大学逻辑与智能研究中心，重庆400715）

［摘要］推荐系统是目前解决用户信息过载的主要工具，协同过滤算法是推荐系统中应用最为广泛的技术，它主要依赖用户已有的历史数据为其寻找有相似的其他用户，然而，当遇到新用户第一次访问的情况下，这类技术一般很难给出恰当的推荐，这就是著名的用户冷启动问题。运用判断聚合理论的技术手段把已有用户的行为数据聚合成为集体判断集，然后将这个集体判断集推送给新用户，新用户根据自身的偏好购买感兴趣的物品，这一方法既解决了新用户的冷启动问题，又丰富和拓展了推荐系统的功能。

［关键词］判断聚合模型；推荐系统；冷启动；协同过滤

1　问题的提出

随着互联网技术的发展和应用，人类从信息匮乏时代步入了信息过载的时代。为了解决信息过载问题，科学家们已经开发出了一系列解决方案，例如搜索引擎技术就是非常成功的案例。然而，当用户无法确切地描述自己的需求时，搜索引擎就无法帮助他们找到适合的信息，此时需要一项技术通过分析用户的历史偏好，然后据此推荐适合的信息，这项技术叫做推荐系统（Recommender Systems，RSs）[1]，它可以将用户和产品很快联系起来，让用户可以在海量的物品中找到适合的物品，并且使物品找到合适的用户。

协同过滤算法是应用最为广泛的推荐系统技术，它是1992年由Goldberg等人提出的。基于用户的协同过滤算法以用户为研究对象，寻找与目标用户有着相似兴趣的用户集合，然后将集合中用户喜欢的，但目标用户不曾听说的物品推荐给他[2]。然而，当一个新用户第一次使用该网站，由于缺乏可用的历史数据，基于用户的协同过滤算法无法给新用户推荐物品，推荐系统对新用户失效，这就是用户的“冷启动”问题。目前，学者们对用户冷启动问题进行了大量的研究，例如，Sahebi和Cohen提出运用社交网络数据解决用户冷启动问题[3]；Park和Chu提出了一个预测特征回归模型来解决冷启动问题等[4]。

判断聚合模型（judgment aggregation model）[5]将集体决策放入更为一般的逻辑框架之内进行研究，更加明晰地揭示了逻辑与集体决策之间的密切联系。给定议程A=｛a，b，c…｝和个体集U=｛u1，…，un｝，个体根据自己的偏好对议程A中的议题进行判断得到个体判断集，模型以个体判断集作为输入，通过判断聚合机制得到集体决策，判断聚合机制通常表现为特定的判断聚合规则。

本文将利用判断聚合模型刻画集体决策过程，把已有用户的行为数据进行聚合形成一个集体判断集，然后将这个集体判断集推荐给新用户，进而解决用户冷启动问题。为此，本文要首先基于命题逻辑建立判断聚合模型，然后选择一组有历史数据的用户，在此基础上，运用判断聚合模型将已有用户的历史数据聚合成为集体判断集，最后将这个集体决策结果推送给新用户。

2　基于判断聚合模型的协同过滤算法

设计基于判断聚合模型的协同过滤算法来解决用户冷启动问题，主要是以网站中已有的其他用户的行为数据为输入，通过判断聚合机制将这些个体的意见或者评价聚合成为集体的意见或者评价，然后将这个集体的意见推荐给新用户，算法如图1所示：

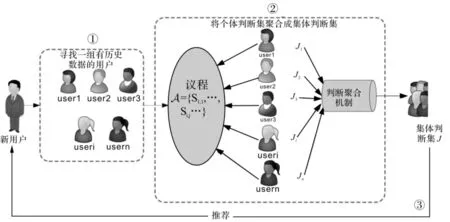
（图1）　基于判断聚合模型的协同过滤算法

从图1中我们可以看到，基于判断聚合模型的协同过滤算法包括三个阶段：第一阶段，寻找一组有历史数据的用户，将他们的用户-物品评分矩阵输入到计算模块；第二阶段，建立判断聚合模型将用户-物品评分矩阵转化成为个体判断集，然后运用判断聚合规则将个体判断集聚合成为集体判断集；第三阶段，将集体判断集推荐给新用户，从而解决用户的冷启动问题。我们现在分阶段说明基于判断聚合模型的协同过滤算法。

第一阶段：寻找一组有历史数据的用户

根据孔多塞陪审团定理（Condorcet Jury Theorem）[6]，即当所有的个体都是独立的且他们有同等做出正确决定的概率，那么个体越多，集体做出正确决定的概率就越大，并且随着个体数量的增多，集体做出正确决定的概率随之增加直至趋向1，换句话说，集体通常做出正确决定的概率远远大于个体，该条定理说明了集体决策通常比个体更加明智，我们假设新用户总是愿意采纳之前用户提供的建议，因此，首先我们需要找到一组有历史数据的用户，这是实现新算法的第一步。

假设目标用户张三在之前从未访问过该网站，我们需要围绕目标用户找到一组有历史数据的用户，如果张三进行了注册，我们可以获取少量关于他的数据，例如性别、IP地址或者是年龄，通过这些信息，我们可以匹配一些和他年纪相仿、性别相同并且处于同一个地区的一组用户；如果张三通过Facebook、Twitter、QQ或者微博微信等账户进行关联登录，我们可以获取部分他公开的有共同兴趣爱好的好友、他所感兴趣的微博或者Twitter话题等信息，通过了解这些信息，我们可以匹配一些与他有相似兴趣的一组有历史数据的用户。然而，很多时候目标用户既没有注册数据又没有用其他的社交网络账户关联登录，此时我们可以单纯凭借IP地址的定位来随机选择一组与目标用户同一地区的用户作为参照，但要求这些用户的数据一定是足够可以做出集体决策的，过于稀疏的数据会导致整个算法失效。

第一阶段主要目标是寻找一组有历史数据的用户作为目标用户的参照，一般来说为了避免平局的情形我们选择多于三个有历史数据的用户并且最好数目为单数。

例1：假定目标用户是张三，根据上述选择参照用户的方法，选定五位参照用户形成一个临时的集体，U=｛u1，u2，u3，u4，u5｝，他们均对五种物品有过购买记录并且有过评分，物品集I=｛I1，I2，I3，I4，I5｝，用户-物品评分矩阵如表1所示，5分表示用户对物品的满意程度最高，1分表示用户对物品的满意程度最低。

第二阶段：基于判断聚合模型得到集体判断集

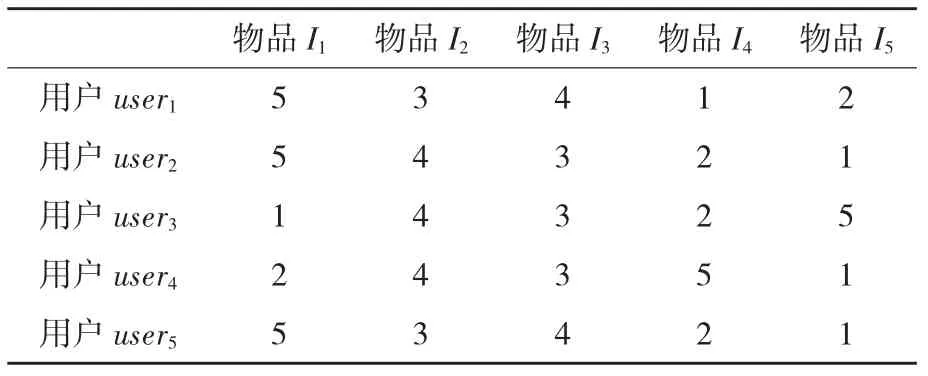
（表1）　　用户-物品评分矩阵

判断聚合模型用于改造协同过滤算法，是本文探索的新方法。运用基于判断聚合模型的协同过滤算法，首先要将用户-物品评分矩阵按照判断聚合模型的定义转变为判断组合，然后利用判断聚合规则将个体判断集聚合成为集体判断集，最后将这个一致的集体判断集推荐给新用户，从而解决用户冷启动问题。

2.1判断聚合模型

选定有历史数据的用户集U=｛u1，…，un｝（n≥3），即有历史数据的用户至少要3人，I=｛I1，…，Im｝（m≥2）为非空的物品集。假设有历史数据的用户都对命题逻辑系统L中的命题进行了判断，L中包含原子命题p，q，r，……，所有复合命题都由原子命题和命题联结词┐（否定）、∧（合取）、∨（析取）、→（实质蕴涵）等命题连接词组成，L中也包含矛盾式⊥（contradiction），以及它的否定重言式（tautology）。

判断聚合模型一个基本的假设是：参与判断的所有用户都是完全理性的，即作出的判断既是一致的又是完全的。所谓一致的是指作出的判断不能具有矛盾，所谓完全的是指对于所有待断定的命题都要作出判断。相关概念定义如下：

议题（Issues）指待判断的命题。显然，议题可以是L中除了矛盾式外的任一命题。议题既不可以是重言式，也不可以是矛盾式，因为它们没有判断的必要。

议程（Agenda）由议题以及议题的否定形式构成的集合称作议程，记作A。本文中议程A=｛SIi，j|Ii∈I，1≤j≤|I|｝∪｛┐SIi，j|Ii∈I，1≤j≤|I|｝，议题SIi，j表示用户给物品集I中的任一物品Ii打j分，如果物品集中一共有5件物品，那么用户对物品Ii的评分最低为1分最高为5分。为了编程的方便，我们在文中减少了下标的数量，用Si，j取代SIi，j表示用户给物品集I中的任一物品Ii打j分，即SI i，j简记为Si，j。

预议程（Pre-agenda）由议题本身构成的集合称为预议程，记作［A］。为了文中论述方便，预议程中只包含议题本身并不包含它们的否定，即［A］=｛SIi，j|Ii∈I，1≤j≤|I|｝。

限制条件（Constraints）是参与判断用户在对议程中议题判断时应遵循的条件，用Γ表示。Γ是L中的一个公式，即Γ∈L，本文中Γ=∧｛┐（Si，j∧Si，j′）|i∈I，j≠j′，1≤j，j′≤|I|｝∪∧｛┐（Si，j∧Si′，j）|i，i′∈I，i≠i′，1≤j≤|I|｝。为了得到一致且完全的个体判断集，限制条件要求用户给每一种物品打出唯一的一个分数，系统不接受一个物品有两个分数和两个物品有相同的分数的情况。

判断集（Judgment set）是与个体和集体相关的概念，用J表示。令U是参加判断的用户，U=｛u1，...，un｝（n≥3），则任一用户uk（1≤k≤n）的判断集是一个一致的且完全的集合。判断集Jk是Γ-一致当且仅当，一致性保证了个体或集体所作出的判断都是理性的；同时Jk是完全的当且仅当对于议程［A］中的任一议题φ∈［A］，要么φ∈Jk要么┐φ∈Jk，判断集的完全性保证了个体对议程中每一项议题都作出判断。本文中将所有Γ-一致且完全的判断集记作D（A，Γ）。

判断组合（Judgment profile）由所有个体的判断集组成的n元组称作判断组合，可表示为P=（J1，…，Jn）∈Dn（A）。我们用N（P，Si，j）表示判断组合P中有多少个用户的判断集中包含有Si，j，也就是N（P，Si，j）=#｛k|Jk∈P，Si，j∈Jk｝。

定义1判断聚合规则（Judgment aggregation rules）令U是参加判断的用户集，议程A⊆L，一个判断聚合规则是以所有个体的判断集构成的n元判断组合P=（J1，…，Jn）（Jk∈D（A，Γ））为输入，输出一个在A和Γ上非空的集体判断集J。

2.2基于判断聚合模型的集体决策过程

根据判断聚合模型的定义，预议程［A］=｛S1，1，...，Si，j，....｝，限制条件Γ=∧｛┐（Si，j∧Si，j′）|i∈I，j≠j′，1≤j，j′≤|I|｝∪∧｛┐（Si，j∧Si′，j）|i，i′∈I，i≠i′，1≤j≤|I|｝，我们将用户-物品评分矩阵变形为|U|×|I|2的判断组合，纵列为选定的有历史记录的用户集U，横行为物品Ii的所有可能的得分Si，j，根据模型中的定义若user1给I1打5分，那么在判断组合中user1与S1，5交叉的空格里标上“1”，其余与S1，1、S1，2、S1，3和S1，4交叉的空格里都为“0”。换而言之，由评分矩阵转变为判断组合的过程是所有用户对议题的判断过程。每位用户根据自己的偏好给出他们对所有议题的判断，用“1”表示赞同，“0”表示反对。

例2：仍用例1中选定的用户集U和物品集I，根据判断聚合模型预议程为［A］=｛S1，1，S1，2，...，S5，5｝，即所有用户要对这些议题进行判断，而且限制条件为Γ=∧｛┐（Si，j∧Si，j′）|i∈I，j≠j′，1≤j，j′≤|I|｝∪∧｛┐（Si，j∧Si′，j）|i，i′∈I，i≠i′，1≤j≤|I|｝。根据上述分析，我们将表1的用户-物品评分矩阵转变为表2的判断组合P。

从判断组合P可以看到每一位用户的个体判断集：user1的个体判断集为J1=｛S1，5，S2，3，S3，4，S4，1，S5，2｝，这个判断集中没有两个物品有同样的分数，也没有一个物品有两个分数的情形，即J1是Γ-一致的，同时user1对议程A中的所有议题都进行了判断，因而J1也是完全的，J1既是一致又是完全的，因而，user1是理性的用户。同理，user2的个体判断集J2=｛S1，5，S2，4，S3，3，S4，2，S5，1｝，user3的个体判断集J3=｛S1，1，S2，4，S3，3，S4，2，S5，5｝，user4的个体判断集J4=｛S1，2，S2，4，S3，3，S4，5，S5，1｝，user5的个体判断集J5=｛S1，5，S2，3，S3，4，S4，2，S5，1｝，这些判断集中没有两个物品有同样的分数，也没有一个物品有两个分数的情形，即它们都是Γ-一致的，且对议程A中的所有议题都进行了判断，因而这些个体判断集都是完全的，这些个体判断都是一致又是完全的，故而，这些用户是理性的用户，所有用户的个体判断形成判断组合P=（J1，…，J5），现在选定一种判断聚合规则将这些个体的判断集聚合成为集体判断集，为了最大化地保留所有个体的判断信息，我们选用最常用的多数聚合规则[7]。

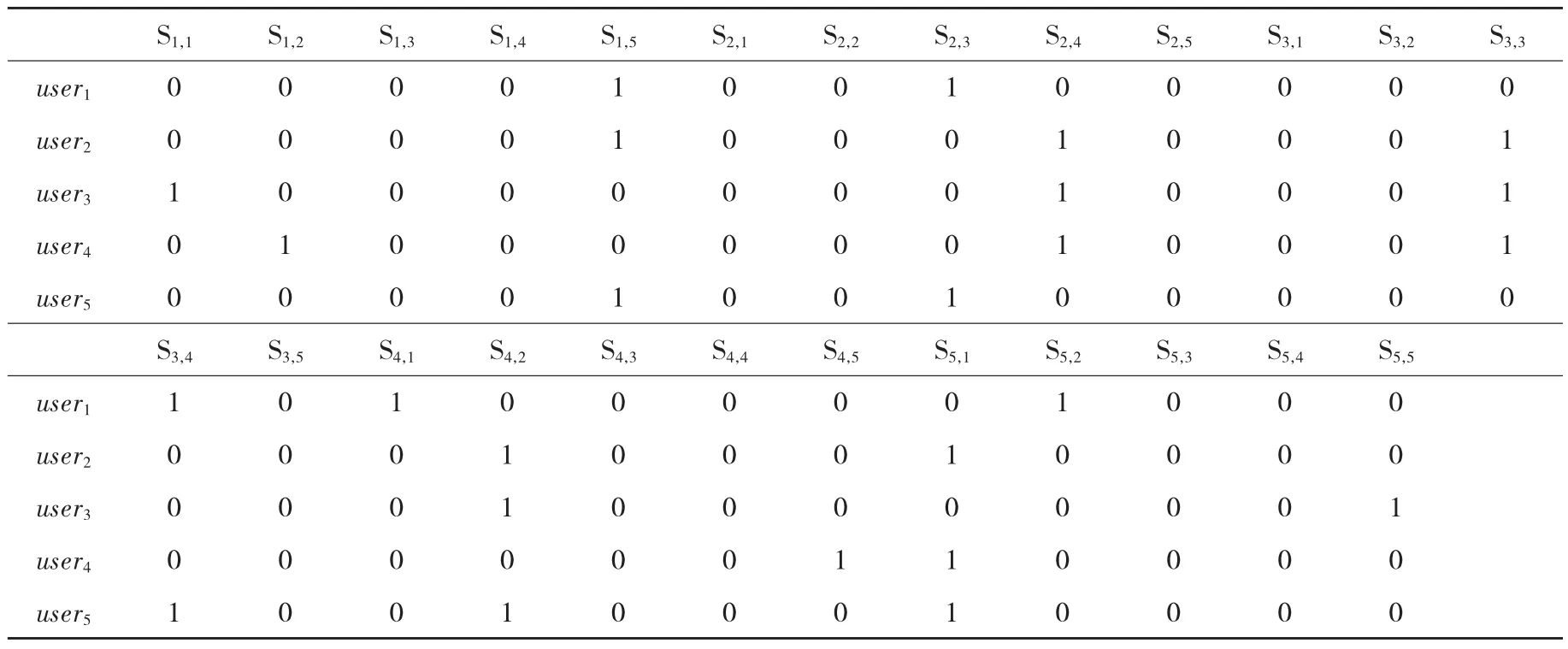
（表2）　判断组合P

定义2多数聚合规则（Majoritartian aggregation rule）输出的判断集是由多数人赞成的议题构成，即对任一J∈D（A，Γ），J=｛Si，j∈A|N（P，φ）>n/2｝，多数聚合规则记作Fmaj，由多数聚合规则得到的集体判断集记作JFmaj。

运用多数聚合规则求得例2的集体判断集，判断组合P如上表2中所示，首先求得所有议题的支持人数，结果如下：

N（P，S1，1）=1；N（P，S1，2）=1；N（P，S1，3）=0；N（P，S1，4）=0；N（P，S1，5）=3；N（P，S2，1）=0；N（P，S2，2）=0；N（P，S2，3）=2；N（P，S2，4）=3；N（P，S2，5）=0；N（P，S3，1）=0；N（P，S3，2）=0；N（P，S3，3）=3；N（P，S3，4）=2；N（P，S3，5）=0；N（P，S4，1）=1；N（P，S4，2）=3；N（P，S4，3）=0；N（P，S4，4）=0；N（P，S4，5）=1；N（P，S5，1）=3；N（P，S5，2）=1；N（P，S5，3）=0；N（P，S5，4）=0；N（P，S5，5）=1。

根据上述对每一项议题的支持人数，可得到过半数用户支持的议题组成的集体判断集为｛S1，5，S2，4，S3，3，S4，2，S5，1｝，即集体判断集JFmaj=｛S1，5，S2，4，S3，3，S4，2，S5，1｝，这个集合中既不存在两个物品有同样的分数，也不存在一个物品有两个分数，即JFmaj∪｛Γ｝是推不出矛盾的，因此，JFmaj是Γ-一致的，同时集体判断集JFma j中对A所有议题都进行了判断，因此是JFmaj完全的，所以JFmaj是一致且完全的集体判断集，它可以作为集体决策执行下去。

2.3程序演示

我们用.NET平台开发的演示程序包含三个表：第一个表输入用户-物品评分矩阵，第二个表是将用户-物品评分矩阵转化为包含所有个体判断集的判断组合，第三个表输出经过聚合机制之后得到的集体判断集，输出的集体判断集也即是给新用户的推荐内容。

如图2所示，第一个表中输入用户-物品评分矩阵，以例1中的用户-物品评分矩阵为例，第二个表中是基于判断聚合模型将第一个表中矩阵转化为判断组合P，并同时在sum一行中计算出所有议题的支持人数，在第三个表中运用多数聚合规则之后得到的集体判断集，用黑色方框标注集体对所有的物品的评分。

第三阶段：将集体判断集推送给新用户

在第二阶段中，运用判断聚合模型将个体判断集聚合成为集体判断集，第三阶段的主要任务是将这个集体判断集推送给新用户。

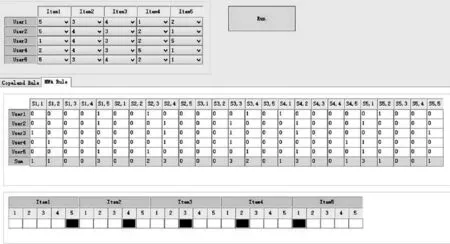
（图2）　基于判断聚合模型运用多数聚合规则得到集体判断集的推荐过程

在判断聚合模型上，运用多数聚合规则得到的集体判断集为JFmaj=｛S1，5，S2，4，S3，3，S4，2，S5，1｝，这个集体判断集提供了两方面的信息：第一，我们可以得到集体对物品集中物品的偏好排序，即这组选定的参照用户集认为I1是最好的，其次是I2、I3和I4，最差的是I5，这表明大多数用户最喜欢I1，I2、I3和I4次之，最不喜欢I5；第二，判断聚合模型得出的集体判断集也同时给出了集体对每一类物品的精确评分，即集体给I1打5分，I2打4分，I3打3分，I4打2分，以及I5打1分。

在推荐阶段将这个集体偏好序推荐给新用户张三，张三也可以根据集体判断集进行个性化的选择：第一，他会从集体判断集中的物品里挑选自己感兴趣但从未购买过的物品；第二，集体判断集表明集体认为I1是最好的，其次是I2、I3和I4，最差的是I5，对于得分最高的I1，如果他感兴趣他会毫不犹豫地购买，而对于I2、I3和I4他可能需要了解更多信息才决定购买，但对于大家都不喜欢的I5，他可能感兴趣但可能不会购买。如此一来，我们不仅解决了用户冷启动问题，而且实现了新用户个性化的推荐。

3　结论

本文基于判断聚合理论的技术手段尝试解决了推荐系统中用户冷启动的问题，从文中的探索来看，可以得出以下结论：第一，基于判断聚合模型的协同过滤算法来解决用户冷启动问题是以系统中已有用户的历史数据为输入，通过分析已有用户的历史数据输出新用户个性化的推荐内容；第二，基于判断聚合模型的协同过滤算法不仅可以得到集体对物品的偏好排序，而且可以得到集体对物品的评分，这些内容可以为新用户提供更为精确的个体决策依据。

［附注］本文受到西南大学人文社会科学重要研究项目（编号：12XDSKZ003）的资助。

[参考文献]

[1]Kantor P B，Rokach L，Ricci F，et al.Recommender systems handbook[M].Berlin：Springer，2011.

[2]Goldberg D，Nichols D，Oki B M，et al.Using collaborative filtering to weave an information tapestry[J].Communications of the ACM，1992，35（12）.

[3]Sahebi S，Cohen W W.Community-based recommendations：a solution to the cold start problem[M]//Proceedings of the 2011 ACM Conference on Recommender Systems.New York：ACM Press，2011.

[4]Park S T，Chu W.Pairwise preference regression for cold-start recommendation[M]//Proceedings of 3rd ACM conference on Recommender systems.New York：ACM Press，2009：21～28.

[5]List C，Pettit P.Aggregating sets of judgments：An impossibility result[J].Economics and Philosophy，2002，18（1）.

[6]Wit J.Rational choice and the Condorcet jury theorem[J].Games and Economic Behavior，1998，22（2）.

[7]Laang J，Pigozzi G，Slavkovik M，et al.Judgment aggregation rules based on minimization[M]//Proceedings of the 13th Conference on Theoretical Aspects of Rationality and Knowledge.New York：ACM Press，2011：238～246.

［责任编辑：熊显长］

［收稿日期］2015-10-09

［作者简介］李莉（1980-），女，内蒙古巴彦淖尔人，西南大学逻辑与智能研究中心2011级博士研究生；唐晓嘉（1954-），女，广西全州人，西南大学逻辑与智能研究中心教授、博士生导师，主要从事现代逻辑与人工智能研究。

［中图分类号］B81

［文献标志码］A

［文章编号］1001－4799（2016）02－0040－05