转化策略在解题中的应用

◇　山东　苏　坤　王晓云



转化策略在解题中的应用

◇山东苏坤王晓云

转化是解数学题的一种重要的思维方法．那么怎样转化呢?概括地讲,就是把复杂问题转化成简单问题,把抽象问题转化成具体问题,把未知问题转化成已知问题．善于观察、联想是进行解题转化的前提,本文介绍解题转化的几个基本策略．

1根据函数结构特点转化为函数性质问题

A7;B8;C9;D10

2几何问题代数化,思维方式的转化

Aa2+b2≤1;Ba2+b2≥1;

解法1点M(cosα,sinα)的轨迹为圆x2+y2=1,由直线与圆有公共点等价于圆心到直线距离小于或等于半径.

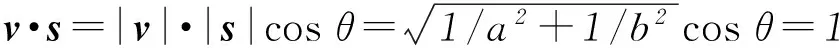
3代数问题几何化,数与形的转化

r2-2(a+b)r+ab=0.

①

(1-2r)a2+(2r2+2r)a-4r2=0,

②

则式②必须有正实根．因为2r2+2r>0,-4r2<0,故式②无2个负根或零根情况,要有正实根,只需Δ=(2r2+2r)2+16r2(1-2r)≥0,化简得r2-6r+5≥0,解得

r≥5或r≤1.

③

因为r<{a,b}min,当且仅当a=b时,{a,b}min取得最大值3,故r<3.

④

4引入辅助量转化命题结构

转化与化归是常用解题方法,对于任何一道数学题,都包含一定的数学条件和关系．要想解决它,就必须依据题目的具体特征,对题目进行深入、细致、透彻的观察,然后认真思考,透过表面现象看其本质,这样才能正确转化解题思路,找到解题方法．

(作者单位：山东省寿光中学)