醇在水中的无限稀释扩散系数的分子动力学模拟*

李志伟，赖舒慧，高 伟，陈六平

(1. 肇庆学院化学化工学院，广东 肇庆 526061；2. 中山大学化学与化学工程学院，广东 广州 510275；3. 广东药学院药科学院，广东 广州 510006)

醇在水中的无限稀释扩散系数的分子动力学模拟*

李志伟1，赖舒慧2，高 伟3，陈六平2

(1. 肇庆学院化学化工学院，广东 肇庆 526061；2. 中山大学化学与化学工程学院，广东 广州 510275；3. 广东药学院药科学院，广东 广州 510006)

采用分子动力学(MD)模拟研究了0.1 MPa、298～318 K条件下甲醇、乙醇、1-丙醇在水中的无限稀释扩散系数(D12)，并通过径向分布函数、配位数、平均氢键数的计算，分析了二元流体的微观结构和分子间的相互作用。结果表明，模拟所得的无限稀释扩散系数与实验值符合。另外，随着温度升高，径向分布函数的峰高、醇分子与水分子之间的配位数以及醇-水的平均氢键数均减小，表明在较高温度下醇分子周围堆积的水分子数减少，醇分子和水分子之间的相互作用力降低，因而使扩散系数增大，这些结果从微观角度解释了扩散系数的变化规律。

分子动力学模拟；醇；水；无限稀释扩散系数

扩散系数是描述传质过程的基本物性数据，在各种化学、化工过程中有重要的作用，其大小与物质的种类和温度有关，在二元体系中还与溶质的浓度有关[1]。流体的扩散系数虽然可通过实验测量获得，但测量过程不仅耗时，而且对于一些高温高压的极端条件，测量难度很大，准确度也不高。因此，通过理论方法来获得扩散系数引起了广泛关注。其中，分子动力学(molecular dynamics，MD)模拟是常用方法，具有明显的优势，不仅可以模拟各种常规和极端条件下的扩散行为，获得扩散系数，还可以得到流体的微观结构性质，从微观角度揭示扩散现象的本质，从而揭示系统中分子扩散与流体微观结构之间的关系。醇类化合物是化工中常见的有机溶剂，在实际的化工生产中，往往需要将不同溶剂按比例混合使用，以增强溶剂的溶解性和选择性。因此，对醇的二元体系的扩散系数和结构性质进行研究有重要的现实意义。

目前已有很多工作研究了单组分醇及醇的二元体系的扩散行为。Hao等[2]采用泰勒分散法测得25 ℃下甲醇、乙醇、1-丙醇、1-丁醇、1-戊醇、1-己醇等水溶液的二元互扩散系数。Wakeham[3-4]对不同浓度的乙醇和水、丙醇和水的二元体系，测得了25～65 ℃下的扩散系数。结果表明，扩散系数受浓度的影响，对于乙醇-水体系，扩散系数在摩尔分数为0.3时有最小值；对于丙醇-水体系，扩散系数在摩尔分数为0.2附近出现最小值，在0.9附近扩散系数出现最大值。此外，MD模拟的方法来研究醇类混合物的热力学性质和结构性质。Bálint等[5]用SPC/E-OPLS力场模拟了不同浓度的甲醇-水混合体系，并提出了更为精确的氢键网络拓扑结构，认为在甲醇浓度低时，氢键通过环状结构相互连接，而随着甲醇浓度的增加，支链慢慢增多。Hasse等[6]采用不同模型组合模拟了甲醇和乙醇水溶液的动力学性质和结构性质，其扩散系数和黏度的模拟结果的平均相对偏差为5%～20%。杨林等[1]曾模拟计算了293.15 K、0.1 MPa下含醇溶液的无限稀释扩散系数。本文拟采用MD模拟计算0.1 MPa、298～318 K条件下甲醇、乙醇、1-丙醇在水中的无限稀释扩散系数，并通过径向分布函数、配位数、氢键等的计算阐明醇-水二元体系的微观结构性质。

1 模型和方法

模拟中，醇分子用OPLS-AA力场描述[7]，具体参数见表1，2，3。水分子采用SPC-Fm模型描述[8]，为更好地符合水分子的实际运动情况，模拟中添加了分子柔性并考虑了键长键角的分子内部运动，其分子内的相互作用势能的形式和具体参数分别如式(1)和表4所示。

表1 OPLS-AA力场键伸缩参数和键弯曲参数

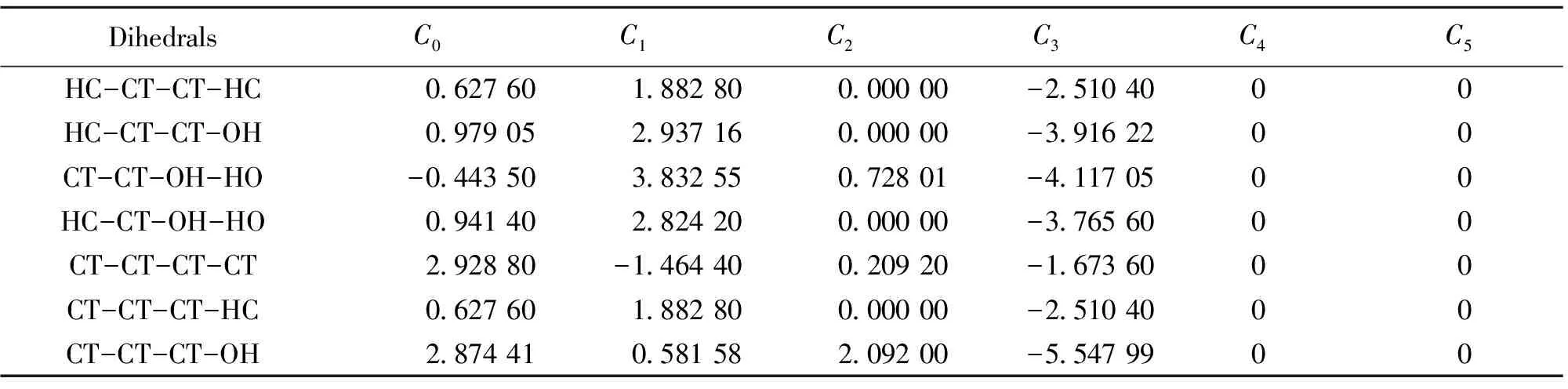
表2 OPLS-AA力场二面角扭曲参数

表3 OPLS-AA力场的非键结势能参数1)

1)a:该原子表示的是甲基上的碳原子；b:该原子表示的是亚甲基上的碳原子。

表4 水分子模型参数

(1)

模拟通过GROMACS程序包完成[9]。模拟在NPT系综中进行，采用了双精度、周期性边界条件、V-rescale的控温方法和Berendsen控压方法，各分子的起始速度采用Maxwell分布。体系采用最速下降法使能量最小化，用蛙跳算法求解体系的牛顿运动方程，截断半径取1.4 nm，采用Particle-Mesh Ewald(PME)法计算长程静电相互作用力，时间步长为1 fs。总的模拟时间为6 ns，其中前3 ns的时间用于体系的平衡，平衡后统计后面3 ns的运动轨迹。溶剂选用的分子数为5 000，醇的质量分数不超过1%，对应的醇分子的个数见表5。

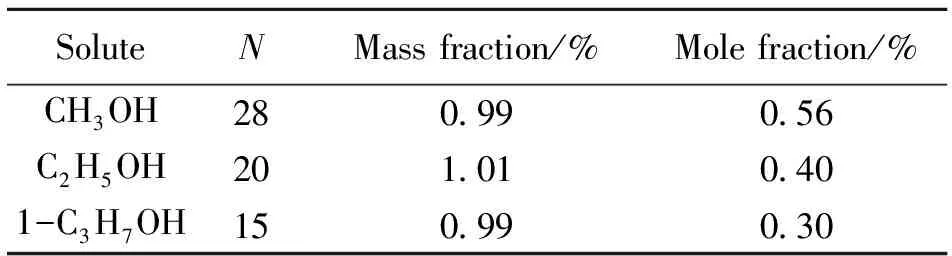
表5 醇-水体系中溶质的分子数、质量分数和摩尔分数

2 结果与讨论

模拟值与相应的实验值列于表6，从表6可知，不同文献测得的扩散系数不同，但相同条件下彼此间相差不大，本文的模拟值和实验值都很吻合，偏差最大的为6%。杨林等[1]采用SPC-OPLS的刚性模型研究了293.13 K、0.1 MPa下甲醇、乙醇、1-丙醇在水中的无限稀释扩散系数，相对偏差依次为36%、11.8%、18.8%。本文采用的是柔性模型，所得结果的相对偏差大大降低。可见，SPC-Fm柔性模型可扩展运用到二元体系中，对扩散系数的模拟结果比刚性模型要好。

图1依次为甲醇、乙醇、1-丙醇分子质心和水分子质心的径向分布函数随温度的变化，表7则列出了径向分布函数的特征值。径向分布函数反映了体系粒子的疏密程度，从而反映出体系的微观结构。峰强度越大，说明O原子周围能够找到H原子的可能性更大，即分子和分子堆积越来越紧密，说明分子运动更加困难，因此扩散系数减小。从图1可看出，随着温度的升高，第一峰位置(rmax)稍微向右移动，峰高(g(rmax))减小，意味着分子堆积越来越稀疏，将使扩散系数增大。在MD模拟中，配位数(CN(rmin))的含义是粒子在距离r内周围能找到的粒子个数，粒子和粒子之间不需要直接结合，可通过对径向分布函数积分得到。配位数越大，说明溶质分子附近堆积的溶剂分子数越多，自然会阻碍溶质分子的运动，使扩散系数减小。表7的数据表明温度增加，CN(rmin)减小，扩散系数将增大，这与扩散系数的随温度升高而增加的变化规律也是一致的。此外，随着碳原子增多，配位数也增多，说明醇附近堆积的水分子增多，阻碍了醇的运动，导致其扩散系数减小。可见，径向分布函数和配位数的数据很好地解释了温度升高扩散系数增大以及大分子醇的扩散系数比小分子醇小的现象。

表6 醇在水中无限稀释扩散系数的模拟值与实验值的比较

Table 6 Comparison of simulated infinite dilution diffusion coefficients of alkanols with experimental values 10-9m2·s-1

alkanols298KExp MD308KExp MD313KExp MD318KExp MDmethanol1 54[2]，1 56[10]1 591 89[11]1 892 10[11]2 222 35[12]2 48ethanol1 22[2]，1 24[4]1 151 57[4]，1 53[12]1 571 80[4]，1 69[12]1 832 01[4]，1 91[12]1 951-propanol1 05[2]，1 02[3]1 061 32[3]1 30-1 671 68[3]1 78

表7 醇-水分子质心径向分布函数特征值和配位数CN

图1 不同温度下醇-水分子质心径向分布函数Fig.1 The radial distribution functions between the mass centers of alkanols and water molecules at different temperatures

本文还研究了二元体系的氢键作用，判断是否存在氢键采用了几何标准[13]，即当O---O距离小于0.35 nm，H---O距离小于0.25 nm和H-O---O夹角小于30°时，认为形成了氢键。表8列出了不同醇-水体系中醇-醇、醇-水、水-水的平均氢键数。从表8可见，醇-醇的平均氢键数很小，说明氢键作用很弱，这主要是由于醇在水中是无限稀释的，因此醇-醇之间几乎没有氢键作用。水-水的平均氢键数为3.5左右，和纯水中计算得的平均氢键数基本相同。文献[5]也指出，在低含量的甲醇溶液中，水分子形成环状结构交缠在一起。本文的模拟结果也说明在醇浓度很低的情况下，水-水的四面体氢键网络结构占主导。值得一提的是，醇-水之间的氢键数大于2，这和Noskovt等[14]在低含量下计算的醇-水平均氢键数是一致的。此前我们课题组计算的纯醇体系中醇-醇之间的平均氢键数约为2[15]，而本文计算的醇-水之间的平均氢键数大于2，说明醇与水之间更容易形成氢键。其主要原因是，醇上的烃基供电子性质使得羟基氧原子上的电子云密度比水中的氧原子大，O-H键更强，因此不容易与另一个醇分子的氧原子形成氢键。氢键数越小，说明溶质分子和溶剂分子之间的作用越小，因而扩散的阻力越小，扩散系数越大。表8的结果表明，对同一体系，随温度升高，醇-水的平均氢键数减少，醇分子和水分子之间的相互作用力就越小，因而扩散系数就越大。所以从氢键的角度也很好地解释了扩散系数的变化规律。

表8 溶液中醇-醇、水-水和醇-水之间的平均氢键数

3 结 论

本文采用MD模拟研究了醇类化合物在水中的分子扩散，计算了醇在水中的无限稀释扩散系数，并通过径向分布函数、配位数、平均氢键数的计算，分析了二元流体的微观结构和分子间的相互作用。无限稀释扩散系数的模拟值与实验值符合，说明本文的方法和模型能有效用于流体扩散系数的研究。另外，径向分布函数、配位数、平均氢键数的计算从微观层面解释了二元体系中溶质扩散的一般规律。随着温度升高，径向分布函数的峰高(g(rmax))、醇分子与水分子之间的配位数(CN(rmin))以及醇-水的平均氢键数均减小，这些数据均表明随着温度升高，醇分子周围堆积的水分子数减小，醇分子和水分子之间的相互作用力降低，因而扩散系数增大，从微观角度很好地解释了扩散系数的变化规律。

[1] 杨林, 袁其朋, 杨晓进. 含醇溶液中分子扩散系数的分子模拟[J]. 高校化学工程学报, 2006, 20(2):296-299.

[2] HAO L, LEAIST D G. Binary mutual diffusion coefficients of aqueous alcohols. Methanol to 1-heptanol [J]. J Chem Eng Data, 1996, 41(2): 210-213.

[3] PRATT K C, WAKEHAM W A. The mutual diffusion coefficient for binary mixtures of water and the isomers of propanol [J]. P Roy Soc A:Math Phys, 1975, 342(1630): 401-419.

[4] PRATT K C, WAKEHAM W A. The mutual diffusion coefficient of ethanol-water mixtures: determination by a rapid, new method [J]. P Roy Soc A:Math Phys, 1974, 336(1606): 393-406.

[6] GUEVARA-CARRION G, VRABEC J, HASSE H. Prediction of self-diffusion coefficient and shear viscosity of water and its binary mixtures with methanol and ethanol by molecular simulation [J]. J Chem Phys, 2011, 134(7): 074508.

[7] JORGENSEN W L, TIRADO-RIVES J. The OPLS [optimized potentials for liquid simulations] potential functions for proteins, energy minimizations for crystals of cyclic peptides and crambin [J]. J Am Chem Soc, 1988, 110(6): 1657-1666.

[8] MIZAN T I, SAVAGE P E, ZIFF R M. Molecular dynamics of supercritical water using a flexible SPC model [J]. J Phys Chem, 1994, 98(49): 13067-13076.

[9] van der SPOEL D, van MAAREN P J, CALEMAN C. GROMACS molecule & liquid database [J]. Bioinformatics, 2012, 28(5): 752-753.

[10] DERLACKI Z J, EASTEAL A J, EDGE A V J, et al. Diffusion coefficients of methanol and water and the mutual diffusion coefficient in methanol-water solutions at 278 and 298 K [J]. J Phys Chem, 1985 (24):5318-5322.

[11] LEE Y E, LI S F Y. Binary diffusion coefficients of the methanol/water system in the temperature range 30-40 ℃[J]. J Chem Eng Data, 1991, 36(2): 240-243.

[12] LI S F Y, ONG H M. Infinite dilution diffusion coefficients of several alcohols in water [J]. J Chem Eng Data, 1990, 35(2): 136-137.

[13] 张宁, 李维仲, 陈聪,等. 氢键准则在DMSO水溶液中应用的评价 [J]. 物理化学学报, 2013, 29(9):1891-1899.

[14] NOSKOV S Y, LAMOUREUX G, ROUX B. Molecular dynamics study of hydration in ethanol-water mixtures using a polarizable force field[J]. J Phys Chem B, 2005, 109(14): 6705-6713.

[15] FENG H, GAO W, SUN Z, et al. The self-diffusion and hydrogen bond interaction in neat liquid alkanols: a molecular dynamic simulation study [J]. Mol Simul, 2014, 40(13): 1074-1084.

Molecular dynamics simulation of infinite dilution diffusion coefficients for several alkanols in H2O

LIZhiwei1,LAIShuhui2,GAOWei3,CHENLiuping2

(1. College of Chemistry and Chemical Engineering, Zhaoqing University,Zhaoqing 526061, China;2. School of Chemistry and Chemical Engineering,Sun Yat-sen University, Guangzhou 510275, China;3. School of Pharmacy, Guangdong Pharmaceutical University, Guangzhou 510006, China)

The infinite dilution diffusion coefficients (D12) of some methanol, ethanol, and 1-propanol in water under the condition of 0.1 MPa and 298～318 K were simulated by molecular dynamics (MD) simulation. The microscopic structure and the intermolecular interaction was also analyzed by calculation of the radial distribution function, coordination number (CN) between the center mass of solute and solvent molecules, and the average number of hydrogen bond of this system. The simulated values are in accordance with that of experiment. In addition, the peak height of radial distribution function, coordination number, and average number of hydrogen bond all decrease with the increase of temperature, indicating that the accumulated water molecules around alkanol molecule decrease and the interaction between alkanol and water reduce. These factors jointly enhance diffusion coefficient. In general, this work provides a reliable simulation method for transfer properties of solutes in water. At the same time, the results are helpful for one to deeper understand the relationship between microscopic structures of fluid and its transfer properties.

molecular dynamics simulation; alkanol; water; infinite dilution diffusion coefficient

10.13471/j.cnki.acta.snus.2016.04.016

2016-01-19

广东省自然科学基金资助项目(2015A030313705); 广东省自然科学基金资助项目(2015A030310176)

李志伟(1977年生)，男；研究方向：应用量子化学 ；E-mail:lzwgzzd@163.com

O641;O649

A

0529-6579(2016)04-0095-05