一类具时滞与饱和发生率的HIV-1传染病模型的全局稳定性*
杨俊仙, 吴元翠, 闫 萍
(安徽农业大学理学院, 安徽 合肥 230036)
一类具时滞与饱和发生率的HIV-1传染病模型的全局稳定性*
杨俊仙, 吴元翠, 闫 萍
(安徽农业大学理学院, 安徽 合肥 230036)
提出了一类具时滞与饱和发生率的HIV-1传染病模型,分析讨论了无病平衡点E0(T0,0,0)和正平衡点E+(T*,I*,V*)的全局稳定性。通过构造Lyapunov函数和LaSalle不变集原理,证明了当dμ>sγβ,对任意τ≥0,无病平衡点E0(T0,0,0)是全局渐近稳定的;当dμ 时滞;饱和发生率;HIV-1传染病模型;全局稳定性;Lyapunov函数 艾滋病(AIDS)是人体免疫机能遭到艾滋病病毒的破坏,病人患上感染性疾病、恶性肿瘤等。它的病原体是人类免疫缺陷病毒(Human Immunodeficiency Virus,简称HIV), HIV是一种攻击人体免疫系统细胞的慢性病毒,生存于人的血液之中。CD4+T细胞是免疫细胞最丰富的白细胞,是HIV感染的主要目标,这些细胞感染后结构受到破坏,减低了人体抵御感染的能力。因此,掌握病毒和CD4+T细胞的变化规律是很重要的[1]。HIV分为两种类型:HIV-1型和HIV-2型。HIV-2仅局限于非洲的西部,且毒力不强,引起的艾滋病病程较长,症状较轻。目前在世界范围内引起艾滋病毒的是HIV-1,因为它的毒性较强,所以当前对HIV的临床研究主要是以HIV-1为主。由于艾滋病感染人数在全球剧增,引起了各国科学家的广泛关注。医药学、生物学和数学等各方面工作者对该病的治疗和预防都已经做了相应的研究, 其中通过数学模型研究 HIV-1传染病的动力学行为是一种有效的方法。对于HIV-1 感染的研究,最初的模型由Perelson[2]提出,数学模型为: (1) (2) 变量T(t),I(t),V(t) 和参数s,β,μ,α,d,γ的生物意义同系统(1),τ是时滞(τ>0)。 在文[10]中,讨论了系统(2)的无病平衡点E0和正平衡点E+的局部渐近稳定性以及无病平衡点E0的全局渐近稳定性,但并没有给出正平衡点E+的全局稳定性分析。本文旨在文[10]的基础上,通过构造Lyapunov函数和利用LaSalle不变集原理,得到正平衡点E+的全局渐近稳定性。 系统(2)满足初始条件: (3) 定理1 当dμ>sγβ,对任意τ≥0,无病平衡点E0(T0,0,0)是局部渐近稳定的;当dμ 定理2 当dμ 定理3 当dμ>sγβ,对任意τ≥0,无病平衡点E0(T0,0,0)是全局渐近稳定的[10]。 定义函数 易知,对∀z>0,F(z)≥0,且有Fmin=F(1)=0。 定理4 当dμ 证明 令(T(t),I(t),V(t))是系统(2)满足初始条件(3)的任意正解。定义Lyapunov函数: 计算函数W1沿系统(2)的全导数: (4) (5) 则(5)式为 定义 于是 由于 因此 故由LaSalle不变集原理知,正平衡点 在系统(2)中, 令参数s=5,μ=0.01,β=0.000 2,α=0.5,γ=2 400,d=5,τ=4,显然dμ 图1 当dμ 图2 当dμ>sγβ时,无病平衡点E0(T0,0,0)是全局渐近稳定的Fig.2 If dμ>sγβ,the disease-free equilibrium E0(T0,0,0) is globally asymptotically stable 本文研究了一类具时滞与饱和发生率的HIV-1传染病模型,讨论了系统(2)的无病平衡点E0(T0,0,0)和正平衡点E+(T*,I*,V*)的局部渐近稳定性和全局稳定性。证明了当dμ>sγβ,对任意τ≥0,无病平衡点E0(T0,0,0)是全局渐近稳定的[10];当dμ [1] 马知恩,周义仓,王稳地,等.传染病动力学的数学建模与研究[M].北京: 科学出版社, 2004: 259-268. [2]PERELSONA,NELSONP.MathematicalmodelsofHIVdynamicsinvivo[J].SIAMReview, 1999,41(1): 3-44. [3]REGOESRR,EBERTD,BONHOEFFERS.Dose-dependentinfectionratesofparasitesproducetheAlleeeffectinepidemiology[J].ProceedingsoftheRoyalofSociety, 2002, 269(1488): 271-279. [4]SONGXY,NEUMANNAU.Globalstabilityandperiodicsolutionoftheviraldynamics[J].JournalofMathematicalAnalysisandApplications, 2007, 329(1):281-297. [5]HERZANDERSONVM,BONHOEFFERS,ANDERSONRM,etal.Viraldynamicsinvivo:Limitationsonestimationsonintracellulardelayandvirusdelay[J].ProceedingsoftheNationalAcademyofSciences, 1996, 93(14): 7247-7251. [6] 杨俊仙, 闫萍. 一类具饱和发生率的时滞SEIR传染病模型的分析[J]. 中山大学学报(自然科学版), 2015, 54(3): 51-55. [7]BAIRAGIN,ADAKD.GlobalanalysisofHIV-1dynamicswithHilltypeinfectionrateandintracellulardelay[J].AppliedMathematicalModelling, 2014, 38(21/22): 5047-5066. [8]URSZULAF,JANP.Adelay-differentialequationmodelofHIVrelatedcancer-immunesystemdynamics[J].MathematicalBiosciencesandEngineering, 2011, 8(2): 627-641. [9]LIB,CHENYM,LUXJ,etal.AdelayedHIV-1modelwithviruswaningterm[J].MathematicalBiosciencesandEngineering, 2016, 13(1): 135-157. [10]LID,MAW.AsymptoticpropertiesofaHIV-1infectionmodelwithtimedelay[J].JournalofMathematicalAnalysisandApplications, 2007, 335(1):683-691. [11]XUR.GlobalstabilityofanHIV-1infectionmodelwithsaturationinfectionandintracellulardelay[J].JournalofMathematicalAnalysisandApplications, 2011, 375(1): 75-81. [12] 杨若晨, 马明菊, 齐逸飞,等. 含潜伏时滞效应和非线性发生率的SEIR模型的长时间行为[J]. 中山大学学报(自然科学版), 2015, 54(1): 24-29, 36. [13]HALEJK,VERDUYNLUNRLSM.Introductiontofunctionaldifferentialequations[M].Berlin:Springer-Verlag, 1993: 130-166. Global stability of a HIV-1 epidemic model with time delay and saturation incidence rate YANGJunxian,WUYuancui,YANPing (School of Science, Anhui Agricultural University, Hefei 230036, China) A HIV-1 epidemic model with time delay and saturation incidence rate is proposed. The global stabilities of a disease-free equilibriumE0(T0,0,0)andapositiveequilibriumE+(T*,I*,V*)arediscussed.ByconstructingLyapunovfunctionsandLaSalle’sinvariantprinciple,itisshownthatifdμ>sγβ,thedisease-freeequilibriumE0(T0,0,0)isgloballyasymptoticallystable,andifdμ time delay; saturation incidence rate; HIV-1 epidemic model; global stability; Lyapunov functions 10.13471/j.cnki.acta.snus.2016.04.005 2016-01-11 国家自然科学基金资助项目(11201002);安徽省教育厅资助项目(KJ2011Z130) 杨俊仙(1976年生),女;研究方向:微分方程、生物数学;通讯作者:吴元翠;E-mail:wuyuancui@ahau.edu.cn O A 0529-6579(2016)04-0026-05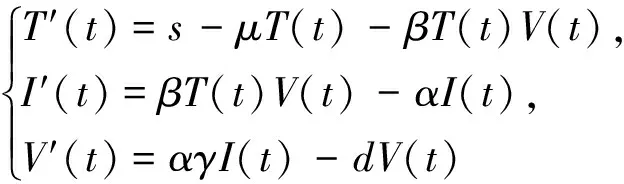


1 平衡点的存在性[10]

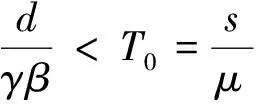
2 无病平衡点E0(T0,0,0)和正平衡点E+(T*,I*,V*)的局部稳定性[10]
3 无病平衡点E0(T0,0,0)和正平衡点E+(T*,I*,V*)的全局渐近稳定性




4 数值模拟



5 讨 论

