对一个几何定点问题的研究与引申

◎周跃佳

(昆明市第三中学，云南 昆明 650500)

对一个几何定点问题的研究与引申

◎周跃佳

(昆明市第三中学，云南 昆明 650500)

2016年我校高三统测卷理科第20题是一个关于椭圆的定点问题.本文通过对该题的解答，抽象出一个椭圆的一般命题，并将其类比到双曲线中.

椭圆；双曲线；定点

一、提出问题

二、结论的推广

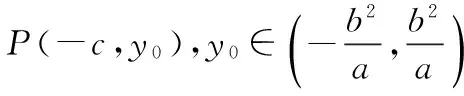
①当直线MN的斜率存在时，设直线MN的方程为y-y0=k(x+c)，M(x1，y1)，N(x2，y2)，

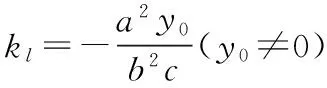
②当直线MN的斜率不存在时，直线MN的方程为x=-c，此时直线l为x轴，也过点(-ce2,0).

综上所述直线l恒过定点(-ce2,0).

三、结论的类比

(同理可证)

[1]付魏.一道解析几何试题的解法研究与变式思考[J].数学通报，2011(11).

[2]苏进文.一道高考题的别证与探究[J].数学教学通讯，2012(03).