浅谈用面积法解线段的相关问题

◎张三华

(西华师范大学 数学与信息学院，四川 南充 637002)

浅谈用面积法解线段的相关问题

◎张三华

(西华师范大学 数学与信息学院，四川 南充 637002)

线段是构成几何图形的重要元素.本文用面积法解初等几何中的线段的线性关系问题和线段的不等问题.

线段；线性关系

初等几何主要研究几何的度量问题和点线的结合问题、线线的平行和垂直问题、点的轨迹问题等.线段的相关问题是初等几何的重要问题.平面几何中多边形可以划分为多个三角形.因此本文用三角形的面积公式解初等几何中的线段的线性关系问题、线段的不等问题.

一、利用面积法解线段的线性关系问题

线段的线性关系是指线段之间的加、减、倍、分的关系.解决线段的线性关系通常把含有多线段的等式的一边,通过作和、作差、作倍、作分等方法表示为一线段，然后转化为相等线段的问题来解决，这种方法往往需要添加多条辅助线，有时由于辅助线的添加不合适，给解决问题带来了一定的困难.用面积法解线段的线性关系时,添加辅助线较少,有时还不需要添加辅助线,直接利用面积公式和线段的关系,就可以解决问题.

例1 如图1，在△P1P2P3中，P1P2=P1P3，P4是边P2P3上的任意一点，P4P5⊥P1P3，P4P6⊥P1P2，P3P7⊥P1P2，求证：P3P7=P4P5+P4P6.

图1

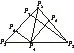
图2

证明 如图2,连接P1P4,由已知有

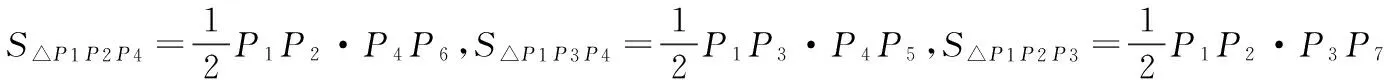
例2 如图3,点P4,P5是边P1P2,P1P3的中点,求证：P2P3=2P4P5.

图3

证明 如图3,由于点P4,P5是边P1P2,P1P3的中点,

所以P1P2=2P1P4,P1P3=2P1P5,P2P3∥P4P5,∠P1P2P3=∠P1P4P5,

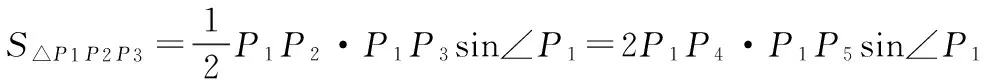
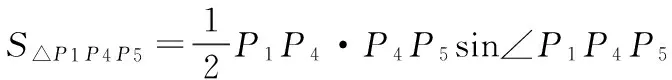
有P1P4·P2P3sin∠P1P2P3=2P1P4·P4P5sin∠P1P4P5,

即P2P3=2P4P5.

二、利用面积法解不等量问题

初等几何中的不等量就是线段的不等关系与角度的不等关系,通常把多个不等量的关系转化为两个不等量的关系.在转化的过程中,需要添加多条辅助线,给解决问题带来了一定的困难.利用面积法解不等量问题,添加辅助线较少,有时还不需要添加辅助线,直接利用面积公式和线段的关系,找到不等量的关系,从而解决问题.

例3 如图4,在△P1P2P3中,P2P4,P3P5分别是边P3P1,P1P2的高线.若P1P2>P1P3,求证：P1P2+P3P5≥P1P3+P2P4.

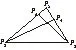
图4

证明 如图4,P2P4⊥P1P3,P3P5⊥P1P2,

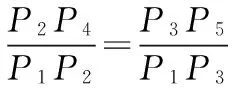
由已知P1P2-P1P3>0,

又P1P2≥P2P4,所以P1P2-P1P3≥P2P4-P3P5,

故有P1P2+P3P5≥P1P3+P2P4.