走进数学建模
张安平

【摘 要】各类数学建模大赛正在如火如荼举行,为了使更多同学了解数学建模,走进数学建模,本文就数学模型、数学建模、建模步骤及建模能力培养谈了一些自己认识。
【关键词】模型;数学模型;数学建模
数学建模是近几年来在我国大学及普通中学中广泛开展起来的一项活动,随着各类数学建模竞赛的举办以及数学建模向数学教学的不断渗透,数学建模活动越来越受到学生和数学教师重视,在教学实践过程中,发现数学建模是创新教育与数学教学最好结合点,数学建模就像一座桥,它将抽象、艰深的数学理论和它在现实生活中丰富多彩的应用连接起来,同学们,尝试着去走走这座桥吧,它将带你走入一个充满挑战和乐趣的世界!
一、数学模型和数学建模
所谓数学模型是指通过抽象和简化,使用数学语言对实际现象的一个近似的刻画,以便于人们更深刻地认识所研究对象,数学模型不是对现实系统的简单模拟,它是人们用以认识现实系统和解决实际问题工具,数学模型是对现实对象的信息通过提炼、分析、归纳、翻译的结果。它使用数学语言精确地表达了对象内在特征,通过数学上演绎推理和分析求解,使得我们能够深化对所研究的实际问题认识。
从这一意义上讲,我们以前在物理学和化学中学习过许多公式,都可以看作一个数学模型。随着数学应用日益广泛,数学模型也越来越多地出现在社会科学及人文科学许多领域。例如,人口增长问题可以用一个指数函数描述并进行预测,某种新产品销售量变化,可以通过一个微分方程来进行解释。
数学建模是指通过对实际问题抽象、简化,确定出变量和参数,并应用某些规律建立起变量与参数间关系的数学模型,求解该数学模型、解释、验证所得的解,确定能否多次循环用于解决实际问题过程,由此可以看出,数学建模是一个创造性的过程,这个过程一般可以分为分析问题、查阅资料、建立模型、求解模型、完善写作等阶段。
二、数学建模一般步骤
建模要经过哪些步骤并没有一定模式,通常与问题性质、建模目的有关,下面介绍是机理分析方法建模一般过程。
1.模型准备
了解问题实际背景,明确建模目的,搜集必要信息数据,弄清对象主要特征,形成一个比较清晰问题,由此初步确定用哪一类模型。
2.模型假设
根据对象特征和建模目的,抓住问题本质,忽略次要因素,作出必要的合理的假设。对于建模成败这是非常重要和关键一步。假设得不合理或太简单,会导致错误的或无用的模型,假设得过分详细,会使你很难或无法继续下一步工作。
3.模型构成
根据所作的假设,用数学语言、符号描述对象的内在规律,建立包含常量、变量等的数学模型,如优化模型、微分方程模型、差分方程模型、图型模型等。
4.模型求解
可以采用解方程、画图形、优化方法、数值计算、统计分析等各种数学方法,特别是数学软件和计算机技术。
5.模型分析
对求解结果进行数学上分析,如对结果误差分析、统计分析、模型对数据的灵敏性分析。
6.模型检验
把求解和分析结果返回到实际问题,与实际的现象、数据比较,检验模型合理性和适用性。
三、数学建模能力的培养
分析问题是完成数学建模关键一步,在分析问题过程中,主要培养学生如何将实际问题与自己所学知识联系起来,学生所学知识都局限于理论知识,理论知识都是在一定理想化条件下得到的,而实际问题很难满足理想化条件,而很多实际问题与理论知识差距较大,如何发现二者关系,就需要学生具备敏锐的洞察力、良好的想象力以及灵感和顿悟,较强的抽象思维和创新意识,使得学生思维的广度、深度、创造性、发散性得到锻炼。
在对问题分析认识基础上,查阅资料能力已变得无比重要,在此过程中学生的阅读理解能力、信息检索能力成为关键。结合对问题分析与查阅的资料,就可以建立数学模型,在此过程中,学生的创新能力、创新思维、创新意识得到充分锻炼。
数学建模最终结果是一篇完整的论文,如何将模型建立、模型求解、算法设计中创新部分有条理表达出来,对提高学生写作能力有较高帮助,通常经过多次训练,学生不仅规范了写作方法,而且激发了他们写作技巧上的创造潜能。
四、数学建模范例
四条腿长度相等的椅子放在光滑但不平坦的地面上,四条腿能否同时着地?
分析:此问题是来源于日常生活中一件普通的事实,把椅子往不平地面上一放,通常只有三只脚着地,放不稳,然而只需稍挪动几次,就可以使四只脚同时着地,放稳了,这个看似与数学无关现象能否用数学语言给以表述,并用数学方法来证实吗?让我们试试看。
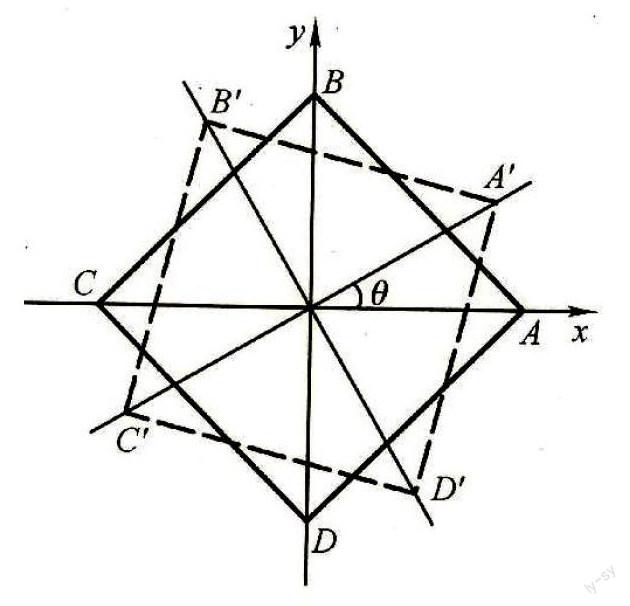
假设椅子中心不动,用A、B、C、D分别表示每条腿的着地点。把连线CA、DB作为X轴和y轴(如图),θ表示对角线AC转动后与初始位置X轴的夹角,y(θ)表示A、C两腿与地面距离之和,f(θ)表示B、D两腿与地面距离之和。
以上例子,仅仅是为同学打开了一扇“数学建模”的窗户,让你看到了数学应用广泛性和趣味性一角,数学作为一门理论性很强学科,并不是如许多人所想象的脱离实际的空中楼阁,其实“生活中处处皆数学”,连结生活和数学的桥梁就是数学建模,同学们,走进数学建模吧!
参考文献:
[1]姜启源等.数学模型[M]北京:高等教育出版社,2003,第三版;
[2]张又昌等.数学[M] 北京:高等教育出版社,2002,第一版;
[3]孙浩.加强数学建模,推动创新教育[J]高等数学研究,2006(6)。

