Theoreticalpredictions ofviscosity ofmethane under confined conditions☆

Yingying Liu,Di Zhou*,Wancheng Zhu*

Department of Chemical Engineering,Qufu Normal University,Qufu 273165,China

1.Introduction

Fluid viscosity is a generalparameter in industrialproductions,which plays a central role in nano flow[1],hydrodynamics[2]and fluid transportation[3].Therefore,the accurate determination of fluid viscosity becomesparticularly important.Generally,the propertiesofconfined fluids display significant differences with bulk fluids,which lead to some restrictive factors of experimental determinations,such as the measurement range,conditions,and so on[4].However,the viscous behaviour of fluids under confinement has not been well understood[5].Consequently,itisextremely necessary to establish a theoreticalmethod to accurately predict the properties and account for the action mechanism.

For a long time,molecular simulation has been a powerful tool to study fluid viscosity from microcosmic point of view.Akhmatskaya et al.[6]adopted the nonequilibrium molecular dynamics simulations to investigate the viscosity ofWeeks–Chandler–Andersen fluids confined in narrow slit pores,and the simulation results matched well with the theoretical ones outside the region of one molecular diameter from the walls.Zhang et al.[7]employed the nonlocal linear hydrodynamic constitutive model[8]and molecular dynamic technique to compute the effective shear viscosity of a simple atomic fluid in a confined channel and obtained approximate streaming velocity pro files in the weak linear regime based on the viscous kernel.Recently,Hoang and Galliero[9]performed molecular dynamic simulations of a Lennard–Jones(LJ) fluid confined in slit pores to study the effects of density inhomogeneous on the shear viscosity pro files.The results show that the local viscosity varied at different position from the walls.Nevertheless,computational limitations,such as system size,truncation of interactions and equilibration time,will affect the accuracy of simulation results.

Theoretically,in order to describe the transport properties of inhomogeneous fluids,Davis[10,11] first proposed a kinetic theory based on Enskog-like kinetic equation.Although Davis's theory accurately predicted the transport coefficients under the confinements of simple slits and cylindrical geometry,it couldn't be extended for application on interfaces or other confined cases.Subsequently,Pozhar and Gubbins[12]developed the modified Enskog theory to overcome these shortcomings.Nevertheless,both ofthe theories are applied to dense,strongly inhomogeneous fluids.Anothersimplertheoreticalapproach to studying the localtransportproperty ofinhomogeneous fluids is the localaverage density model(LADM)[13],in which viscosities of fluids are obtained qualitatively with the equilibrium density pro files.The review of these theories can be found in literature[14].Afterwards,the LADM was revised by combining the configurational viscosity and the translational viscosity,which could be used both for the dilute and dense fluids[9].

In contrast with the above approaches,density functional theory(DFT)has been proved asa reliable approach in the descriptionsofinhomogeneous fluids[15,16].By integrating the modified fundamental measure theory[17]for short-range repulsion and the weighted density approximation[18]for long-range attraction,the DFT can thus be employed for accurate calculation of the density pro files of LJ fluids in confined conditions.In this work,we aim to obtain the density distributions of methane either on solid surfaces or in slit pores with different widths,and also predict its viscosity pro files based on the revised LADM.Besides,the relationship between the local density and viscosity distribution is presented,and the in fluence factors,such as temperature,width pores and different external fields are investigated.

2.Theory

For simplicity,the methane molecule is considered as a spherical molecule.The interactions of methane–methane and methane–wall are described as LJ 12–6 potentials

where εijand σijare the LJ energy and length parameters,respectively.Unlike interaction parameters can be calculated by the Lorentz–Berthelot mixing rules.

2.1.DFT of inhomogeneous system

In general,the grand potentialΩ[ρ(r)]ofa system with the presence of external field can be expressed in the following form

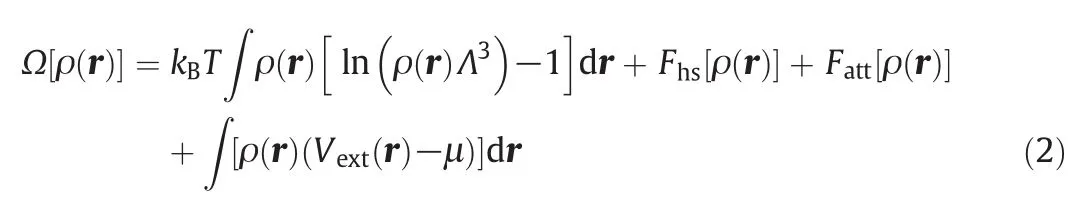
in which ρ(r)represents the density distribution with configuration r,kBis the Boltzmann constant,T is the absolute temperature,Λ is the thermal de Broglie wavelength,Fhs[ρ(r)]and Fatt[ρ(r)]are the local Helmholtz free energies of hard-sphere repulsion and the dispersion attractive contributions,respectively,Vext(r)accounts for external potential,and μ indicates the bulk chemical potential,which can be obtained from ρ(r)=ρb.

According to the modified fundamental measure theory[17],the hard-sphere repulsion contribution can be calculated by

where β=1/kBT,Φhs[nα(r)]is the Helmholtz free energy density of the hard sphere fluid,and can be given as

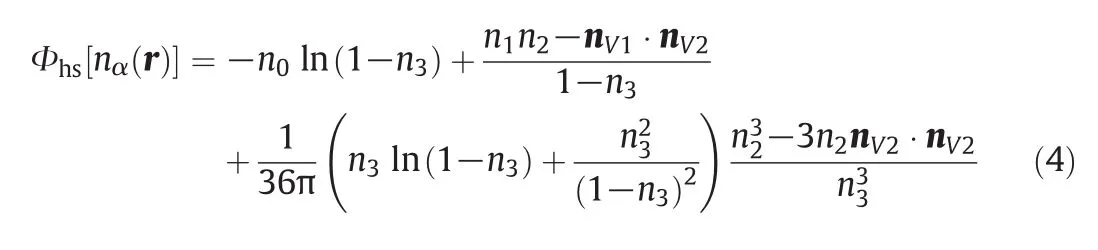
In the above equation,nα(r),α=0,1,2,3,V1,V2,is the weighted density

The details of w(α)can be seen elsewhere[17].

As for the attractive part,Fatt[ρ(r)]can be expressed with the weighted density approximation[18]

whereis the free energy per particle[19],and the weighted densityis defined as

with the weight function ωatt(r)given by

Here catt(r)is the direct correlation function of the bulk density[15].

On the basis of above free energy functionals,minimizing the grand potential leads to the Euler–Lagrange equation

For fluids on uniform walls,the density fluctuations occur only in one direction.Therefore,ρ(r)can be reduced to ρ(z).The above equation can be solved by the Picard iteration.

2.2.Viscosity distributions of inhomogeneous fluids

In order to obtain the viscosity distributions of pure fluids under confined conditions,the shear viscosity is separated into two parts[9]

where ηt(z)is the translational viscosity and ηc(z)indicates the configurational viscosity.ηt(z)relates with the momentum transfer of molecules,and can be expressed as

in which Ωvis the collision integral[20],γ is estimated by

Accordingly,ηc(z)corresponds to the contribution of molecular interactions,and the expression is

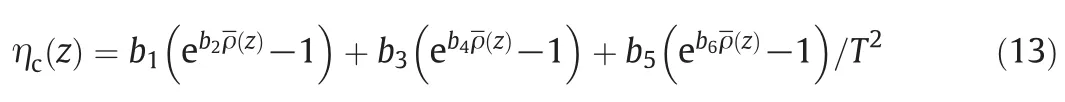
where the parameters bican be taken from Ref.[21].

3.Results and Discussions

In this work,the LJ molecular parameters of methane are selected as the diameter σ=0.373 nm and the energy parameter ε/kB=148.1 K[22].The calculated results are compared with the simulation results to test the accuracy of the theoretical model.

3.1.Inside split pores

The slitlike pore is constructed by two in finite solid plates parallel to the x–y plane.We firstcalculate the density pro files ofa LJ fluid in a split pore of width 10σ at T∗=kBT/ε=2.0 and=0.291.The calculated results and simulation data are both plotted in Fig.1(a).It shows that the density varies with position,and there exists one peak at～1σ from the wall.Based on the density pro files,the corresponding shear viscosity distributions can be obtained in Fig.1(b).The variation trend is similar to the density fluctuations.In the figure,the superscript“*”indicates dimensionless of the variable,andwith the molecular mass m.Furthermore,the viscosity variations of the LJ fluids in pore widths 5σ and 8σ have been shown in Fig.2(a)and(b),respectively.From both Figs.1 and 2,it can be seen that the calculated values under different confined conditions are in excellent agreement with the simulation data[9],which verifies the reliability ofthe theoretical model.

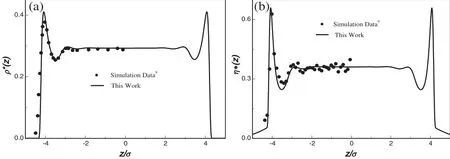
Fig.1.Density pro files(a)and shear viscosity distributions(b)of a LJ fluid at T*=2.0 and=0.291 with the pore width H=10σ.

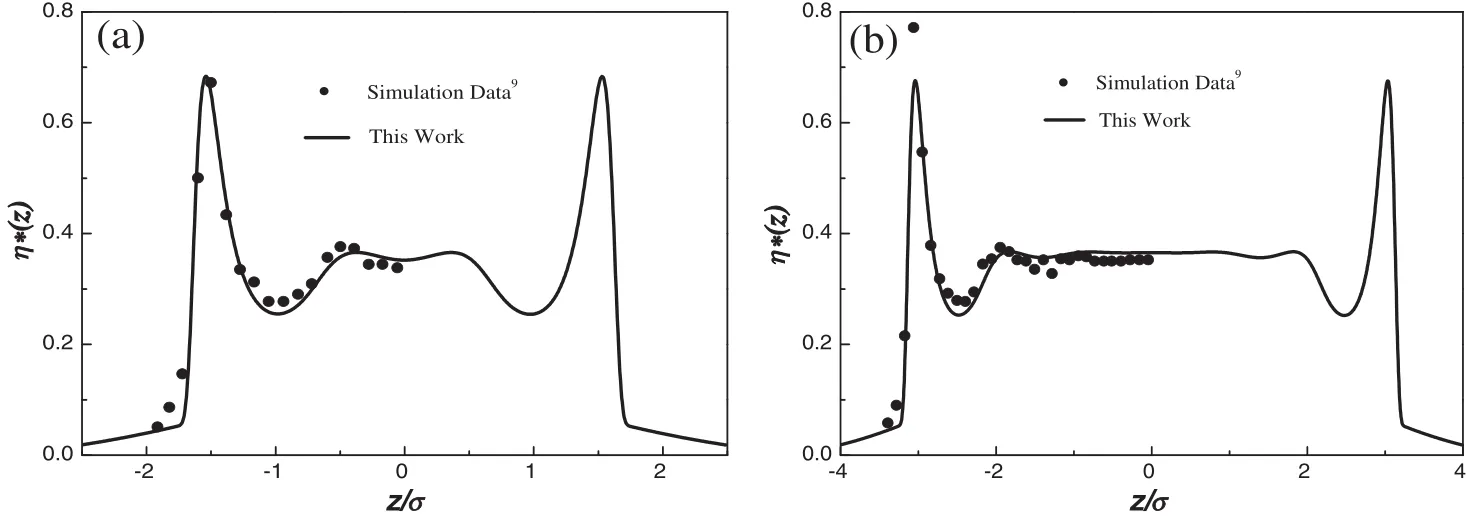
Fig.2.Shear viscosity distributions of a LJ fluid with the pore width H=5σ (a)and H=8σ (b).

In the following,the properties of methane in slit carbon pores are studied.The interaction between methane and the slit wall can be executed as Steele's 10–4–3 potential[22]

in which ρsrepresents the number density of atom in the slit wall,σsfand εsfare the LJ parameters of those between solid and fluid,Δ means the interlayer space of solid atoms.In this work,ρs=114 nm,σsf=0.3565 nm,εsf/kB=21.5 K,and Δ=0.335 nm for the carbon wall[21].For slit pores,the external field can be given by

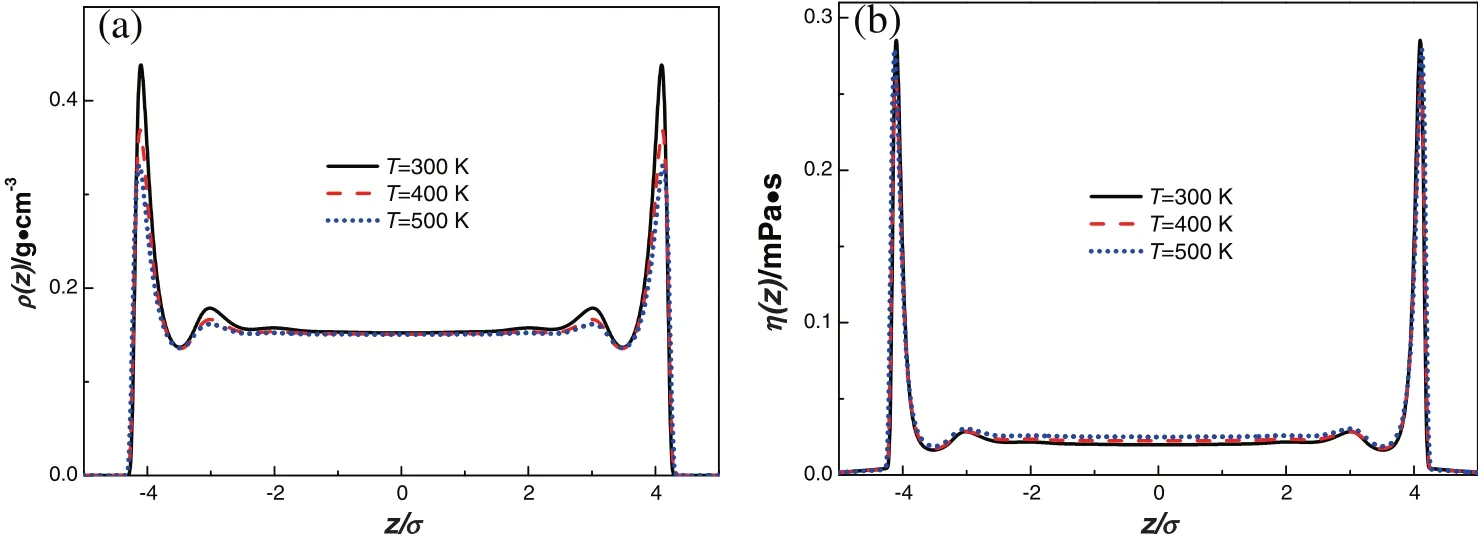
Fig.3.Density pro files(a)and shear viscosity distributions(b)of methane inside the pore of width H=10σ at different temperatures.

Here H is the pore width.In the subsequent calculations,the bulk density of methane is adopted as ρb=0.15 g·cm−3.Firstly,the density pro files of methane in the pore of width H=10σ are obtained at T=300 K,400 K and 500 K and plotted in Fig.3(a).The first peak is remarkable at～1σ from the wall.With the increase in temperature,the peak value of density decreases.The density fluctuations disappear in the middle of the pore,and the value is close to the bulk density.Correspondingly,the shear viscosity distributions are shown in Fig.3(b).The trend of local viscosity looks similar to the density change.However,the first peak value is almost the same.It demonstrates that the effect of temperature on the shear viscosity inside slit pores is unobvious in the condition of the same bulk density.

In addition,the shear viscosity pro files with different pore widths are presented in Fig.4.The widths are H=5σ and H=8σ,and the calculated results are presented in Fig.4(a)and(b),respectively.It can be seen that,the decrease in pore width makes the viscosity fluctuations appear in the middle position of the slit pore,which may be caused by the increase in interactions from the opposite wall.

Fig.4.Shear viscosity distributions of methane with pore widths H=5σ (a)and H=8σ (b)at different temperatures.

3.2.On the hard wall

In order to study the viscosity property of methane under other confined conditions,we also calculate the density pro files and viscosity distributions on the hard wall.The interaction between methane and the hard wall can be expressed by

The calculated results are shown in Fig.5.It reveals that the higher the temperature is,the higher the density becomes within 1σ from the wall(Fig.5(a)).However,a similar pattern on the corresponding shear viscosity has been observed in the whole calculation range(Fig.5(b)).

3.3.On a solvophobic wall

The planar wall consists of one in finite solid plate parallel to the x–y plane,and a solvophobic wall is discussed in the present work.The interaction between methane and the planar wall can be expressed as Steele's 10–4 potential[23].

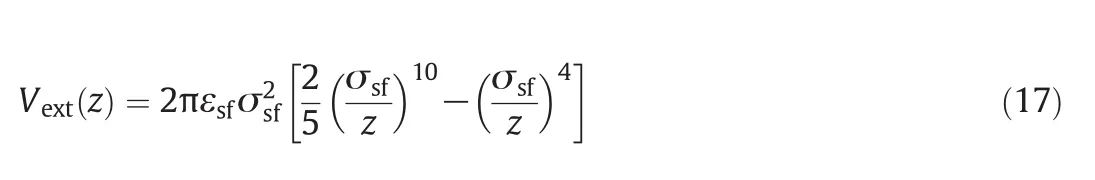
For this wall,εsf/kB=1.481 K.The local density and viscosity on the wallare respectively shown in Fig.6(a)and(b).From the figure,the density and shear viscosity both present a peak at the position～0.5σ from the wall.And the in fluence of temperature on the shear viscosity is remarkable.The shearviscosity increases with the increase in temperature.

Fig.5.Density pro files(a)and shear viscosity distributions(b)of methane on the hard wall at different temperatures.

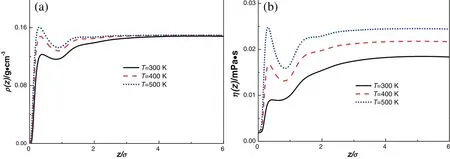
Fig.6.Density pro files(a)and shear viscosity distributions(b)of methane on a solvophobic wall at different temperatures.

4.Conclusions

In summary,the shearviscosities ofmethane on solid surfaces and in the slit pores are predicted based on the density pro files obtained from the DFT.The theoretical results are first verified by the simulation data.The effects of temperature,pore width and interactions between fluid and solid on the shear viscosity are explored in a density state.It demonstrates that the effect of temperature is more obvious on solid surfaces than that in slit pores,and the width of pores will affect the number of peaks.Although some empirical parameters are introduced in the viscosity model,the calculation approach provides a way to determine the viscosity under confined conditions,which is very important in real industrial applications.And we believe that in the near future,this approach can be extended to other complex systems.

[1]H.Zhang,H.Ye,Y.Zheng,Z.Zhang,Prediction of the viscosity of water confined in carbon nanotubes,Micro fluid.Nano fluid.10(2)(2011)403–414.

[2]P.J.Cadusch,B.D.Todd,J.Zhang,P.J.Daivis,A non-local hydrodynamic model for the shear viscosity of confined fluids:analysis of a homogeneous kernel,J.Phys.A Math.Theor.41(3)(2008)035501.

[3]A.Kumar,A.Henni,E.Shirif,Heavy oil viscosity modeling with friction theory,Energy Fuel 25(2)(2011)493–498.

[4]A.Ponjavic,J.Dench,N.Morgan,J.S.S.Wong,In situ viscosity measurement of confined liquids,RSC Adv.5(2015)99585–99593.

[5]S.H.Khan,E.L.Kramkowski,P.J.Ochs,D.M.Wilson,P.M.Hoffmann,Viscosity of a nanoconfined liquid during compression,Appl.Phys.Lett.104(2014)023110.

[6]E.Akhmatskaya,B.D.Todd,P.J.Daivis,D.J.Evans,K.E.Gubbins,L.A.Pozhar,A study of viscosity inhomogeneity in porous media,J.Chem.Phys.106(11)(1997)4684–4695.

[7]J.Zhang,B.D.Todd,K.P.Travis,Viscosity of confined inhomogeneous nonequilibrium fluids,J.Chem.Phys.121(21)(2004)10778–10786.

[8]D.J.Evans,G.P.Morriss,Statistical mechanics of nonequilibrium liquids,Academic,London,1990.

[9]H.Hoang,G.Galliero,Local viscosity of a fluid confined in a narrow pore,Phys.Rev.E 86(2012)021202.

[10]H.T.Davis,Kinetic theory of inhomogeneous fluid:Tracer diffusion,J.Chem.Phys.86(3)(1987)1474–1477.

[11]H.T.Davis,Kinetic theory of flow in strongly inhomogeneous fluids,Chem.Eng.Commun.58(1987)413–430.

[12]L.A.Pozhar,K.E.Gubbins,Transport theory of dense,strongly inhomogeneous fluids,J.Chem.Phys.99(11)(1993)8970–8996.

[13]I.Bitsanis,J.J.Magda,M.Tirrell,H.T.Davis,Molecular dynamics of flow in micropores,J.Chem.Phys.87(3)(1987)1733–1750.

[14]S.K.Bhatia,M.R.Bonilla,D.Nicholson,Molecular transport in nanopores:A theoretical perspective,Phys.Chem.Chem.Phys.13(2011)15350–15383.

[15]Y.Tang,J.Wu,Modeling inhomogeneous van der Waals fluids using an analytical direct correlation function,Phys.Rev.E 70(2004)011201.

[16]D.Zhou,J.Mi,C.Zhong,Three-dimensional density functional study of heterogeneous nucleation of droplets on solid surfaces,J.Phys.Chem.B 116(48)(2012)14100–14106.

[17]Y.-X.Yu,J.Wu,Structures of hard-sphere fluids from a modified fundamentalmeasure theory,J.Chem.Phys.117(22)(2002)10156–10164.

[18]S.-C.Kim,S.H.Lee,A density functional perturbative approach for simple fluids:The structure of a nonuniform Lennard-Jones fluid at interfaces,J.Phys.Condens.Matter 16(36)(2004)6365–6374.

[19]Y.Tang,Z.Tong,B.C.-Y.Lu,Analytical equation of state based on the Ornstein–Zernike equation,Fluid Phase Equilib.134(1–2)(1997)21–42.

[20]P.D.Neufeld,A.R.Janzen,R.A.Aziz,Empirical equations to calculate 16 of the transport collision integrals Ω(l,s)*for the Lennard–Jones(12–6)potential,J.Chem.Phys.57(3)(1972)1100–1102.

[21]G.Galliero,C.Boned,A.Baylaucq,Moleculardynamics study ofthe Lennard–Jones fluid viscosity:Application to real fluids,Ind.Eng.Chem.Res.44(17)(2005)6963–6972.

[22]A.Vishnyakov,E.M.Piotrovskaya,E.N.Brodskaya,E.V.Votyakov,Y.K.Tovbin,Critical properties of Lennard–Jones fluids in narrow slit-shaped pores,Langmuir 17(14)(2001)4451–4458.

[23]T.G.Trudeau,K.C.Jena,D.K.Hore,Water structure at solid surfaces of varying hydrophobicity,J.Phys.Chem.C 113(46)(2009)20002–20008.