New parameter tuning method of washout filter-aided controller for dynamic behavior adjustment☆

Hao Jiang,Nan Zhang,Jinsong Zhao,Tong Qiu,Bingzhen Chen*

Institute of Process Systems Engineering,Department of Chemical Engineering,Tsinghua University,Beijing 100084,China

1.Introduction

Chemical processes contain various reactions with strong nonlinearity and multiplicity[1–4].The stabilities of these multiple steadystate solutions are usually different[5,6].As an important part of operability,stability represents the ability to tolerate small fluctuations and relates to product quality and process safety[7].Since fluctuation is inevitable,stability is widely concerned and studied by academic and industrial community.Lots of efforts have been made to seek a stable operating point or design a control device.However,in some cases,the optimal operating point is on the unstable branch.If we want to achieve the best economic bene fits,designing a control device is a good method.

Traditional PID control and static state feedback control will change the location of original operating point and the equilibrium manifold and cannot tolerate uncertainties.Mönnigmann and Marquardt have introduced the washout filter-aided controller(WFC)to chemical process and proposed a method to deliberately introduce Hopf bifurcations to stabilize parts of the equilibrium manifold of an ODE process model without affecting the equilibrium manifold[8].The advantages of WFC are equilibrium preservation and automatic equilibrium following and facilitating the design of a robust controller[9].However,Mönnigmann and Marquardt's method faces with two major limitations:the dimension of operating variables must be equal to or greater than that of state variables and only one positive real eigenvalue is permitted in the open loop system.Moreover,there is no systematic way to determine the controller parameters[10].To overcome these limitations,we propose a new tuning method in this study for dynamic behavior adjustment via WFC,so that WFC can be a general controller to adjust the dynamic behavior of most chemical processes.With this method,a propanediol anaerobic fermentation is studied.

2.A New Tuning Method

Washout filters can reject steady-state inputs while passing transient inputs[10],and are mainly used in power system and aircraft control[11].The dynamics,output,transferfunction and controllaware listed in Table 1.

In the dynamics,xkis the k th element of the state variables,and d is the reciprocal of the filter time constant.The output is the same as the dynamics,meaning that when steady-state is reached,the output is equal to 0.The control law used in this paper is quite simple,v is the reference input used to determine the actual operating point and w is a controller parameter.

Table 1 Details of washout filters

In Mönnigmann and Marquardt's method[8],there are two assumptions:there is only one positive real eigenvalue in the open loop system and the dimension of operating variables is equalto or greater than that of state variables.In the closed loop system,the dimension is extended to n+1.When one chooses the appropriate controller parameters(d and w),the first n−1 eigenvalues with negative real part can be preserved in the closed loop system and the last two eigenvalues can be assigned arbitrarily.Specifically,we can select the optimal operating point or its neighboring point;its eigenvalues can be assigned to have negative real parts.Thus the optimal operating point is stabilized in the closed loop system.The comparison of the open loop and closed loop systems is listed in Table 2.

Obviously,the assumptions in Mönnigmann and Marquardt's method[8]cannot be satis fied in most chemical processes.Therefore,a new tuning method is developed to obtain the appropriate controller parameters for the stability of a desired operating point.An operating point is stabilized if all the real parts of the eigenvalues are negative,and the accurate value of eigenvalue is not very important to stability.Consequently,an optimization formulation is presented to determine the appropriate controller parameters.

In Eq.(1),the objective is minimizing the maximal real parts of all the eigenvalues in the closed loop system,the optimization variables are controller parameters d and w.~A is the Jacobian matrix of the closed loop system and ε is a given negative number to limit the upper bound of the real parts of the eigenvalues.Eig denotes the eigenvalues and Re denotes the real parts of eigenvalues.The constraint means that all the real parts of the eigenvalues in the closed loop system are negative,and then the stability can be guaranteed.LBdand LBware the low bounds of d and w,UBdand UBware their upper bounds.The lower and upper bounds of optimization variables are not necessary,but if the calculated controller parameters are too large or too small to implement,the lower and upper bounds can ensure the results in reasonable regions.Typically,the initial lower and upper bounds can be set to−5 and 5,respectively.When the optimization has no solution with the initial lower and upper bounds,the constraints can be relaxed until obtaining solutions.The strategy ofstabilizing selected pointis a process of trial and error.Initially,the desired operating point is selected,if the stable region is sufficiently wide and the desired operating point is not too close to the boundary of stable region,the calculated controller parameters are acceptable,otherwise,we mustselectanotherneighboring point and solve the optimization problem until obtaining a satisfactory result.The detailed tuning method is depicted in Fig.1.

Fig.1.Tuning method of WFC.

Table 2 Comparison of the open loop and closed loop systems

3.Case Study

Microbial anaerobic fermentation is an efficient and environmentally friendly process to produce 1,3-propanediol,but the operating point with the highest product concentration is unstable.The WFC is introduced to this process and the parameters are tuned by the method proposed in Section 2.Cell,substrate,and product mass balances of the fermentation process are[12,13]

where

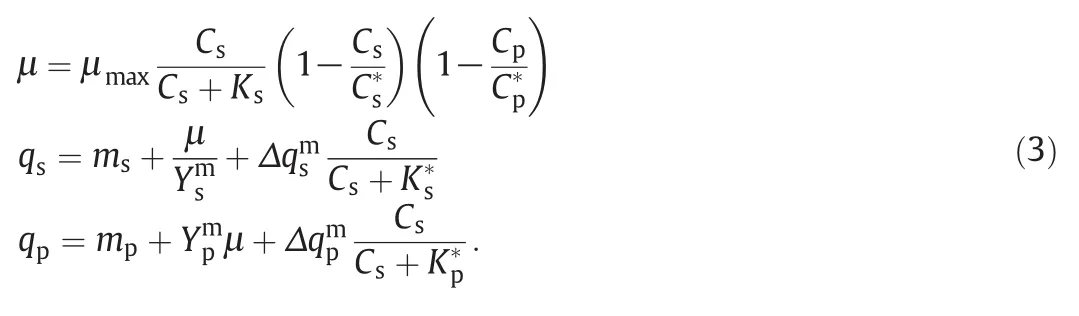
The dimensionless model of 1,3-propanediol fermentation is as follows.

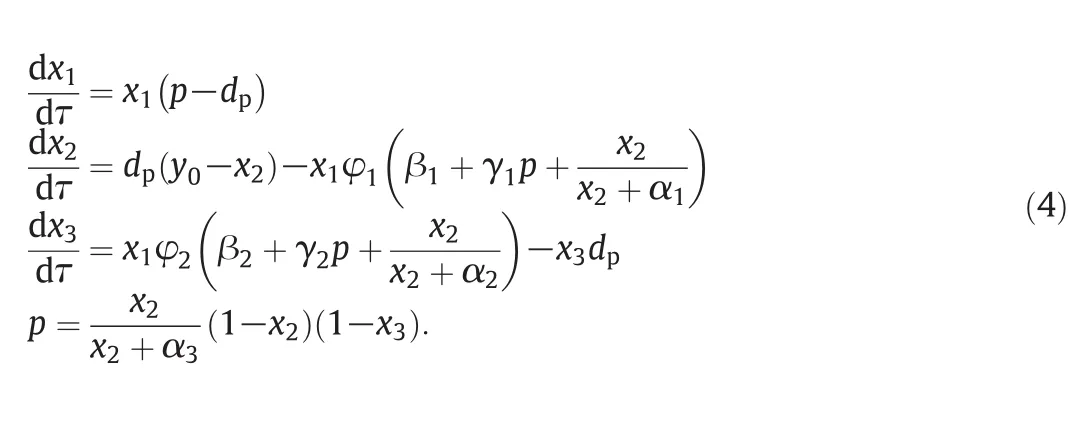
The state variables are x1,x2,and x3,meaning dimensionless concentrations of biomass,substrate and product,respectively.The operating variables are dimensionless dilution rate dpand dimensionless feed substrate concentration y0,and their dimensions are less than that of state variables.The values of the parameters are listed in Table 3.The operating point is optimized to obtain the highest concentration of propanediol,and the optimal operating condition is listed in Table 4.

Table 3 Parameters of 1,3-propanediol fermentation

Table 4 Optimal operating condition

The open loop bifurcation diagram of dimensionless propanediol concentration x3versus dimensionless substrate concentration y0is depicted in Fig.2(a)when the dimensionless dilution rate dpis 0.3.The bifurcation diagram is drawn by the tools developed by Wang et al.[14]and it shows the steady-state solution when parameter changes and the stability of different branches.The bifurcation diagram of the open loop system is consistent with Wang et al.’s result[15].

It can be seen from Fig.2(a)that the optimal operating point is on the unstable branch.To stabilize the unstable optimal operating point,a WFC is introduced to the dimensionless biomass concentration x1.The dynamics of the washout filter and the operating variables can be written as

The controller parameter is calculated at the optimal operating point(dp,y0)=(0.3,0.2744).The upper bound of the real parts of the eigenvalues is set to ε= −0.25.In addition,to insure a solution of the optimization problem,the lower and upper bounds of optimization variables(d and w)are set to−5 and 5,respectively.The optimization result is d=−0.2159,w=[5,−0.5130]T,and the real parts of eigenvalues of the closed loop system at the optimal operating point(dp,y0)=(0.3,0.2744)are listed in Table 5,in which all the real parts are negative,which means that the optimal operating point is stable.The bifurcation diagram of the closed loop system versus the second reference input is depicted in Fig.2(b),showing that a Hopf point is introduced near the optimal operating point and the original unstable equilibrium manifold between the Hopf point and limit point is stabilized without changing the shape of the equilibrium manifold.The Hopf point at point(v2,x3)=(0.2394,0.6896)is supercritical.

To verify the effectiveness of the designed WFC,the set-point tracking curve of the closed loop system near the optimal operating point is illustrated in Fig.3.The curve shows the dynamic performance of the closed loop system when the operating condition is changed.Generally,if the actual value can follow the set value with small overshoot in a short time,the controller is effective.In addition,the actual operating variable changing curves under the control of WFC are illustrated in Fig.4.The actual values of operating variables achieve the new operating condition according to the output of the controller.It should be noted that the operating variables should be manipulated in their reasonable regions all the time,otherwise,the controller becomes unavailable.Initially the process is operated with the optimal reference input(v1,v2)=(0.3,0.2744).The dimensionless product concentration converges to the set value with small overshoot quite rapidly when the reference input changes to(v1,v2)=(0.35,0.265).The tracking performance is also satisfactory when the reference input changes to(v1,v2)=(0.32,0.27).The operating variable changing curves demonstrate that all the actual operating variables are in reasonable regions.These simulated curves show the high tracking speed,smallovershoot and effectiveness ofthe designed controller.

4.Conclusions

This paper proposes a new tuning method of WFC for the dynamic behavior adjustment of chemical processes.By solving an optimization problem,a set of appropriate controller parameters can be obtained,achieving the goal of stabilizing desired operating point.In this method,the limitations of the original method are overcome,so that this general method can be used in most high dimensional chemical systems.Finally,the effectiveness of the improved tuning method is proven by a 1,3-propanediol fermentation process.

Fig.2.Bifurcation diagram.(a)open loop;(b)closed loop.

Table 5 Real parts of eigenvalues of the closed loop system

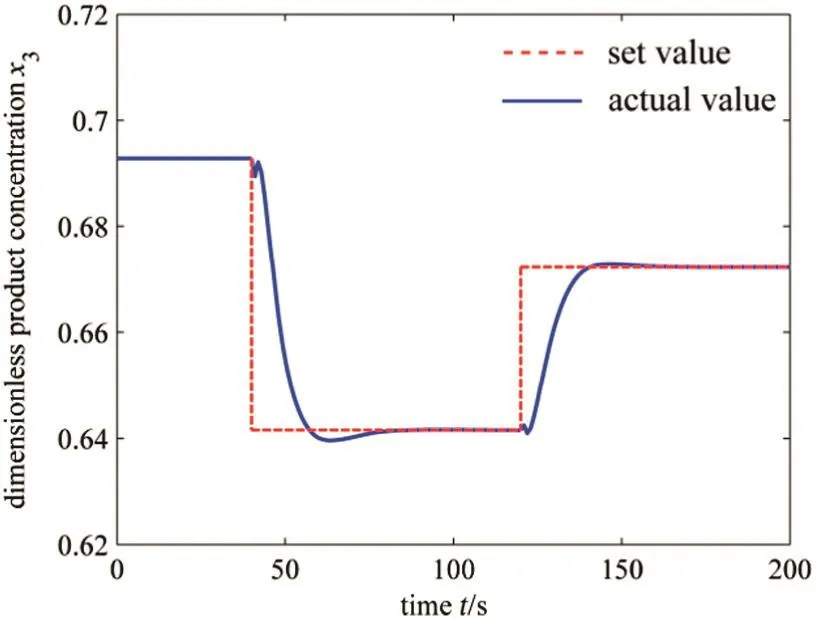
Fig.3.Set-point tracking curve near the optimal operating point.

Fig.4.Operating variable changing curves near the optimal operating point.(a)d p;(b)y0.

Nomenclature

dpdimensionless dilution rate

p dimensionless specific growth rate

x1dimensionless biomass concentration

x2dimensionless substrate concentration

x3dimensionless product concentration

y0dimensionless substrate feed concentration

τ dimensionless time

[1]A.Kuhlmann,D.Bogle,Study on nonminimum phase behaviour and optimal operation,Comput.Chem.Eng.21(1997)S397–S402.

[2]W.D.Seider,D.D.Brengel,A.M.Provost,S.Widagdo,Nonlinear analysis in process design.Why overdesign to avoid complex nonlinearities?Ind.Eng.Chem.Res.29(5)(1990)805–818.

[3]S.S.Elnashaie,J.R.Grace,Complexity,bifurcation and chaos in natural and manmade lumped and distributed systems,Chem.Eng.Sci.62(13)(2007)3295–3325.

[4]H.Z.Wang,Z.H.Yuan,B.Z.Chen,X.R.He,J.S.Zhao,T.Qiu,Analysis of the stability and controllability of chemical processes,Comput.Chem.Eng.35(6)(2011)1101–1109.

[5]L.F.Razón,R.A.Schmitz,Multiplicities and instabilities in chemically reacting systems—A review,Chem.Eng.Sci.42(5)(1987)1005–1047.

[6]A.Uppal,W.Ray,A.Poore,On the dynamic behavior of continuous stirred tank reactors,Chem.Eng.Sci.29(4)(1974)967–985.

[7]H.Jiang,B.Z.Chen,H.Z.Wang,T.Qiu,J.S.Zhao,Novel method for considering process flexibility and stability simultaneously,Ind.Eng.Chem.Res.53(38)(2014)14765–14775.

[8]M.Mönnigmann,W.Marquardt,Bifurcation placement of Hopf points for stabilization of equilibria,Proceedings of the 15th IFAC World,2002.

[9]H.C.Lee,Robust control of bifurcating nonlinear systems with applications(Ph.D.Thesis)University of Maryland,College Park,1991.

[10]M.A.Hassouneh,H.C.Lee,E.H.Abed,Washout filters in feedback control:Bene fits,limitations and extensions,Proceedings of the 2004 American control conference,Boston 2004,pp.3950–3955.

[11]H.C.Lee,E.H.Abed,Washout filters in the bifurcation control of high alpha flight dynamics,American control conference,Boston 1991,pp.206–211.

[12]Z.L.Xiu,A.P.Zeng,W.D.Deckwer,Multiplicity and stability analysis of microorganisms in continuous culture:Effects of metabolic over flow and growth inhibition,Biotechnol.Bioeng.57(3)(1998)251–261.

[13]A.Meel,W.D.Seider,M.Soroush,Game theoretic approach to multiobjective designs:Focus on inherent safety,AICHE J.52(1)(2006)228–246.

[14]H.Z.Wang,B.Z.Chen,X.R.He,J.S.Zhao,T.Qiu,Numerical analysis tool for obtaining steady-state solutions and analyzing their stability characteristics for nonlinear dynamic systems,J.Chem.Eng.Jpn 43(4)(2010)394–400.

[15]H.Z.Wang,N.Zhang,T.Qiu,J.S.Zhao,X.R.He,B.Z.Chen,A process design framework for considering the stability of steady state operating points and Hopf singularity points in chemical processes,Chem.Eng.Sci.99(2013)252–264.