Dynamic interaction analysis and pairing evaluation in control configuration design☆

Xionglin Luo*,Pengfei Cao,Feng Xu

Department of Automation,China University of Petroleum,Beijing 102249,China

1.Introduction

In industrialprocesses,multi-inputand multi-output(MIMO)systems are difficult to control due to the interactions within loops,while decentralized PID control remains dominant since it is easy for operation and maintenance.With decentralized control strategy,a MIMO system is always decomposed into multiple single-input and single-output(SISO)subsystems for which PID controllers are designed independently.However,the interactions between these subsystems exertprofound in fluence on process controland cannotbe ignored.Good controlperformance may not be achieved with stronger interactions between these subsystems.Therefore,the control configuration design,to determine pairing of manipulated(input)and controlled(output)variables to form multi-SISO-subsystems,is the primary problem for decentralized control system.Interaction analysis is the most extensive means to achieve this goal.

Interaction analysis focuses on measuring the extent of interactions within loops and provides the most reliable variable pairing.The relative gain array(RGA)has been widely used forinteraction analysis since its introduction in 1966 by Bristol[1].RGA shows advantages that it is dependenton process models only and independentofthe scaling ofinputs and outputs.With the consideration of the stability of decentralized control systems,the Niederlinski index(NI)is used in conjunction with the RGA based pairing rules[2,3].However,using steady-state gain alone may result in incorrect interaction measures and consequently poor pairing decisions for RGA,since no dynamic information of the process is taken into consideration.To overcome the limitations of RGA method,several dynamic interaction analysis methods have been proposed.

Witcher and McAvoy proposed the relative dynamic array[4]and Gagnepain and Seborg proposed the average relative gain matrix[5]based on the integralofopen-loop step response.Meeuse and Huesman proposed the dynamic RGAwith closed-loop response based on the best achievable control performance using internal model control[6].McAvoy et al.presented a new approach to define dynamic RGA[7],which assumes the availability of a state space model with proportional outputoptimalcontroller designed,and defines the dynamic RGAbased on the controller gain matrix.Through defining the effective relative gain array(ERGA),Xiong et al.presented a new dynamic loop pairing criterion[8–11].The elements of ERGA,which include both steadystate gain and bandwidth information of the open-loop transfer functions,can re flect the dynamic loop interactions under finite bandwidth control.He et al.proposed the relative normalized gain array(RNGA)as a complement to the RGA-NI loop interaction analysis method[12].RNGA investigates both the steady-state gain and normalized the integrated error of outputs for interaction measurement and provides a more comprehensive description of loop interactions.Monshizadeh-Naini et al.defined the effective relative energy array based on the ERGA[13],each element of which is the product of squared zero frequency gain and bandwidth frequency to re flect the effective energy.

There also exist non-square systems extensively in industrial processes with unequal numbers of inputs and outputs[14,15].The nonsquare structure brings new difficulties for control configuration design[16].Most of the interaction analysis methods above cannot be directly applied in non-square systems.Chang and Yu have extended the RGA to non-square systems with more outputs than inputs[17].The closed-loop gain is derived with the assumption of perfect control in least-square sense of which the control objective is to minimize the sum of square errors of all outputs.Then non-square RGA(NRGA)is derived.The system is first squared down,and then pairing is obtained based on the NRGA criterion.Reeves and Arkun have introduced non-square dynamic block relative gain and relative sensitivities as dynamic interaction measures that depend on the controller tuning,which are consequently applicable to the design of non-square decentralized controllers[18].

These interaction analysis methods including those proposed in this paper have their limitations and may not provide the best pairing result for allprocesses[19].Itis necessary to evaluate whether the recommended pairing resultissuitable;ifnot,anotherloop pairing isneeded.However,few literatures have reported the research on pairing evaluation.

In this paper,a new open-loop interaction analysis method foropenloop stable square system is introduced and corresponding pairing criterions are derived.More detailed analysis about non-square system and its main pairing problem are taken,and an interaction analysis method is utilized forobtaining properpairing for non-square multivariable systems.Specific pairing evaluation method is introduced based on closed-loop dynamic relative gain.

2.An Open-loop Interaction Analysis Based on REGA

Using steady-state relative gains of RGA only may result in some incorrect interaction measures and consequently wrong loop pairing decision,since no dynamic information of the process is taken into consideration.A method providing overall evaluation for interactions between control loops is preferred,so a relative energy gain array(REGA)method is proposed here.

Relative gain should include both steady-state and dynamic information of loop interactions.For the interaction analysis method based on REGA,the steady-state information is extracted from the process steady-state gain and the dynamic information is extracted based on step response analysis.

For n×n system,we have transfer function matrix as below.

For ij loop,we can rewrite the transfer function as

Thus the normalized output can be expressed as

Here,the integrated square error criterion of step response is adopted to evaluate the process dynamics

where(∞)represents the final steady-state value of normalized output and θE,ijis defined as control energy consumption.Apparently,a small energy consumption value implies a fast dynamic response for output,while a large one indicates a slow process dynamic response.Generally,the original state is considered steady at t=0 and(0)=0.With the unit step input signal,the normalized output is shown in Fig.1.

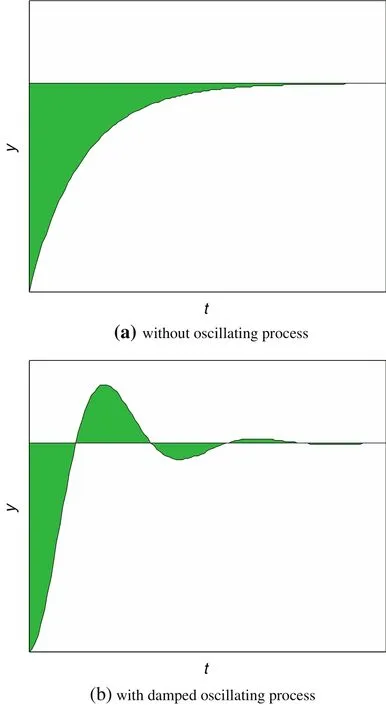
Fig.1.The response curve of normalized output.

In Fig.1 the square of the shaded area refers to the control energy consumption.For most industrial processes,the element of transfer function matrix can be described as first order plus delay time(FOPDT)model

or second order plus delay time(SOPDT)model

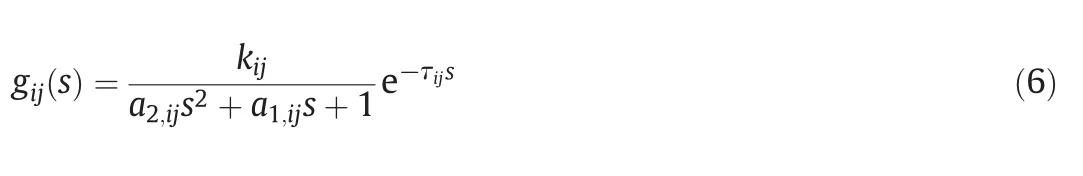
When gij(s)is described as FOPDT modelor SOPDT model,θE,ijcan be obtained as(Appendix A)

or

The steady-state gain gij(0)re flects the steady-state effect ujon yiand θE,ijaccounts for the response speed.With steady-state gain and control energy consumption,energy gain kE,ijbetween yiand ujwith other loop open is defined as

The relative energy gain can be obtained as

where k′E,ijis the gain between yiand ujwith other loops closed.The REGA can be obtained as

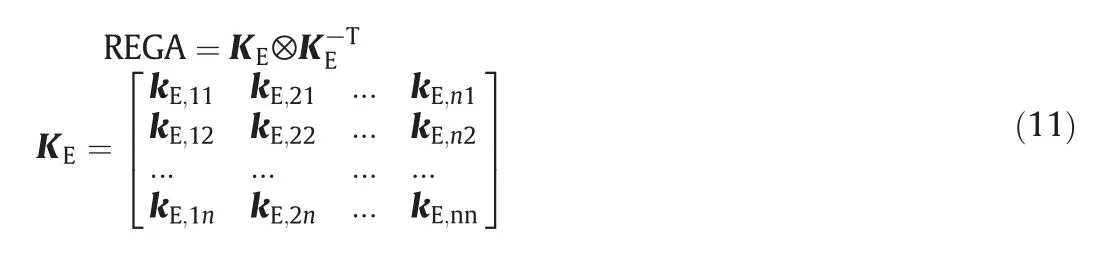
where⊗is the Hadamard product.The pairing criterion based on REGA and NI is developed as

(1)all paired RGA elements are positive;

(2)NI is positive;

(3)the paired REGA elements are closest to 1.0;

(4)large REGA elements should be avoided.

Example 1.For a 2×2 system

According to the analysis method based on RGA and RNGA,no proper pairing is provided.Based on ERGA,the pairing y1−u2,y2−u1is proposed,while based on REGA,the pairing y1−u1,y2−u2is proposed.In order to verify if the pairing is proper,optimal PID controllers are designed by using IMC method[20]for both diagonal and off-diagonal pairings.At time 0 and 33 min,there are unit step changes for setpoints of y1and y2.The comparative simulations are shown in Fig.2.The control performance with diagonal pairing is much better than that with off-diagonal pairing.The method based on REGA provides proper choice for pairing.This example demonstrates the limitation of RGA,RNGA and ERGA that the contributions of response time constant and delay time to process dynamics are not balanced well.

Example 2.For a 3×3 system

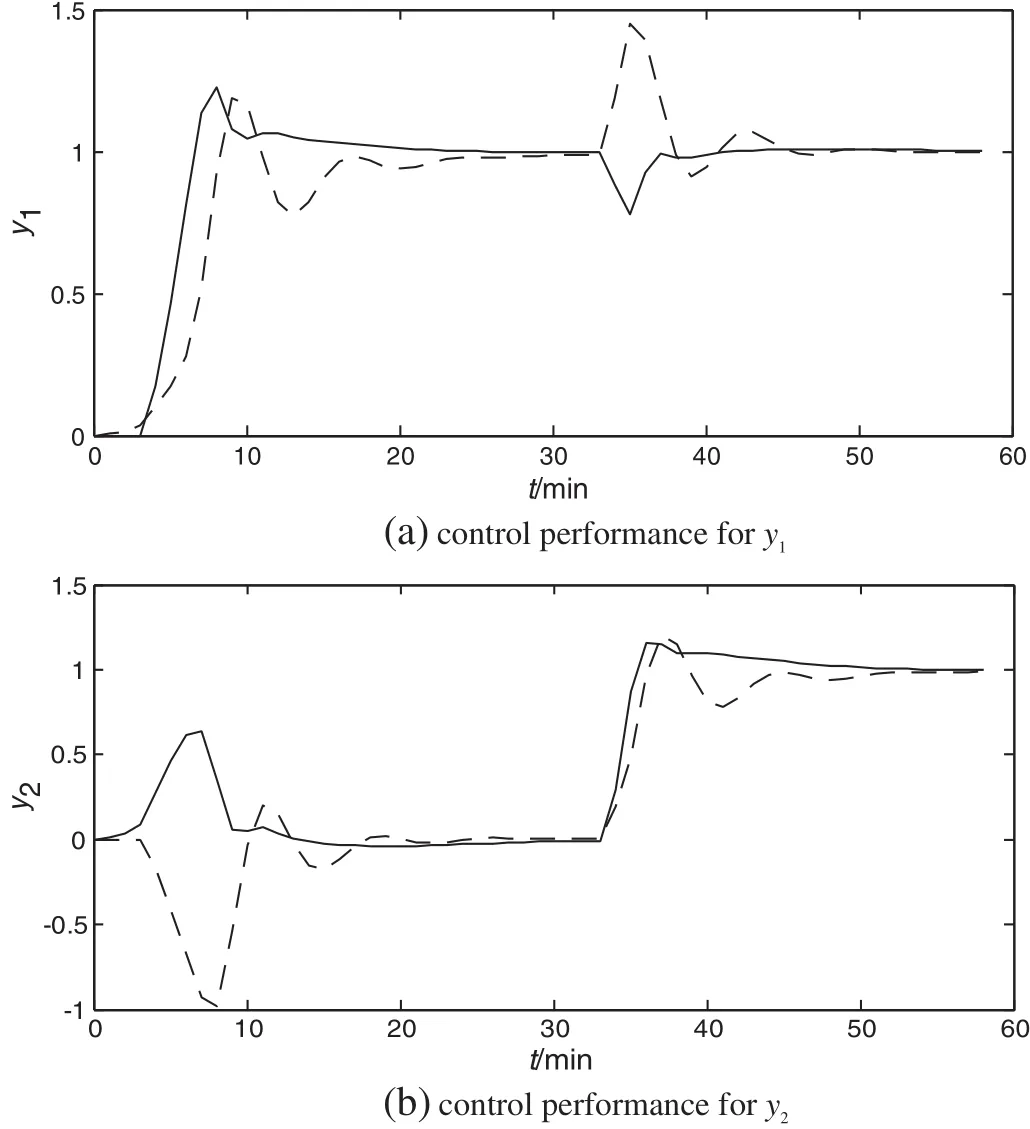
Fig.2.Control performance with two pairings.diagonal pairing;— —offdiagonal pairing.

Based on RGA and RNGA,the pairing y1−u2,y2−u1,y3−u3is proposed,defined as P1.Based on ERGAand REGA,the pairing y1−u1,y2−u3,y3−u2is proposed,defined as P2.In order to verify if the pairing is proper,optimal PID controllers are designed by using IMC method[20]for these two pairings.At time 0,80 and 150 min there are unit step changes for setpoints y1,y2and y3.The comparative simulations are shown in Fig.3.The control performance with pairing P2 is much better than that with pairing P1.The method based on REGA assesses the interactions accurately and provides proper pairing for this system.

3.Interaction Analysis for Non-square Multivariable Systems

Non-square multivariable systems with unequal numbers of inputs and outputs exist extensively in industrial processes and decentralized control is still the main control strategy.However,unequal numbers of inputs and outputs may bring in great difficulties for control configuration design.Therefore,how to pair manipulated variables and controlled ones is a more difficult task for non-square systems.

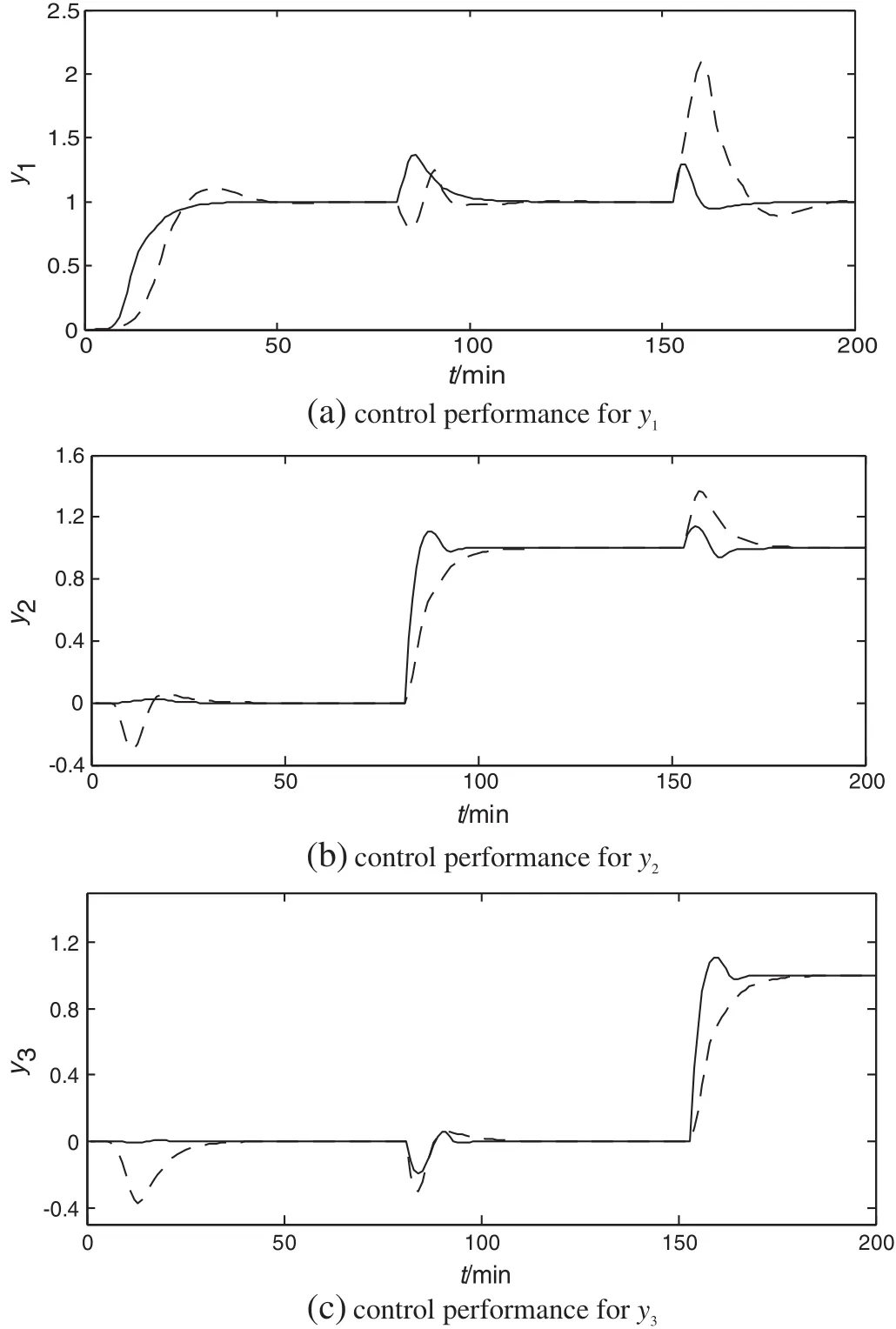
Fig.3.Control performance with two pairings.pairing P2;— —pairing P1.

Assume that the input dimension is m and output dimension is n.There are two non-square systems for industrial processes:the one with m ＞n is a“fat”system;the other with m ＜ n is a“thin”system.Both systems have difficulties for appropriate pairing.There may be more pairing choices for “fat”systems,in which manipulated variables remain and how to pair the rest manipulated and controlled variables are the main problems for “fat”systems.However,since the number of controlled variables is more than manipulated ones for“thin”systems,it seems more difficult to choose proper pairing with some outputs remained without control.Appropriate variable pairing should be obtained in orderto guarantee good controlperformance foralloutputs.

Based on the idea of literature[17],we extend the REGA interaction analysismethod to non-square systems.The core problemisto calculate the pseudo-inverse matrix for KEdefined in Eq.(11),then the nonsquare relative energy gain array(NREGA)can be obtained similar to REGA of Eq.(11).The interaction analysis method for non-square systems is based on NREGA.

When KEis row full rank,we have the pseudo-inverse matrix

When KEis column full rank,we have

Then NREGA can be obtained

Several properties for NREGA are as follows.

(1)When m＜n,the sum of each column elements is equal to 1.

(2)When m＞n,the sum of each row elements is equal to 1.

(3)When m=n,KE+equals KE−1,that is NREGA=REGA.Therefore,the REGA of square system is a special case of NREGA of nonsquare system.

(4)The closer to 1 the element of NREGA is,the smaller the interactions from other loops are.

The pairing method and criterion based on NREGA are as follows.

(1)When m＜n,remove the corresponding inputs of the rows with the smaller sum of all elements to leave the same numbers of inputs and outputs.When m＞n,remove the corresponding outputs of the columns with the smaller sum of all elements to leave the same numbers of inputs and outputs.

(2)Once a newsubsystemwith the same numbers ofinputs and outputs is obtained,calculate the REGA for the subsystem and choose appropriate pairing through the pairing criterion based on REGA.

Example 3.Consider a mixing tank as “fat”system with three input streams and one exit stream[18],as shown in Fig.4.The concentrations of input steams are constants and the outlet valve is fixed.The height of liquid in the tank h and exit concentration cAare controlled variables,and the flow rates of input streams F1,F2and F3are manipulated variables.

Fig.4.A mixer tank.

The 2×3 transfer function matrix can be obtained as

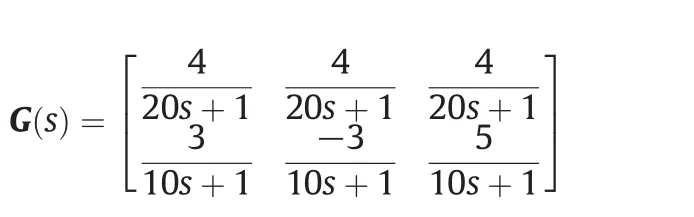
For this “fat”system,we can calculate the NREGA

All sums of each column elements are calculated as 0.3846,0.9615 and 0.6538.According to the squaring method,we remove the first input variable u1.We have the square subsystem as

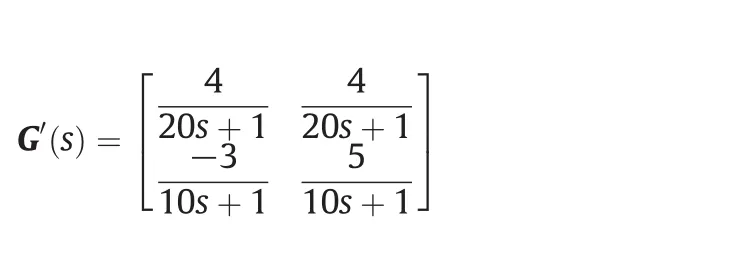
and calculate the REGA as

According to the pairing criterion based on REGA,we have the final pairing y1−u2,y2−u3for this“fat”system.This pairing result is in accordance with the one in literature[18],which has proven that better control performance can be achieved compared to other pairings.

Example 4.Consider a side-stream distillation[17],separating benzene,toluene and xylene,as shown in Fig.5.The concentrations of four impurities in three product streams are controlled by three manipulated variables:reboiler duty,re flux ratio and side stream flow rate.

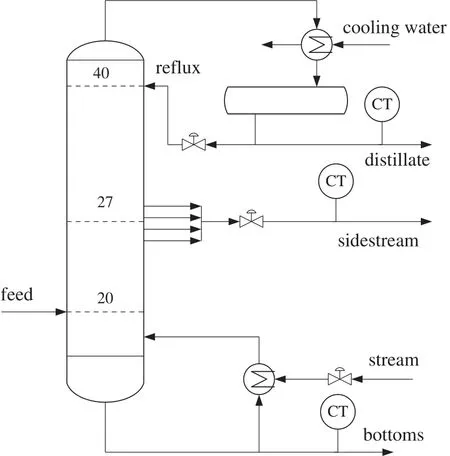
Fig.5.Distillation column.

The transfer function matrix can be obtained as shown in Table 1.For the “thin”system,we can calculate the NREGA

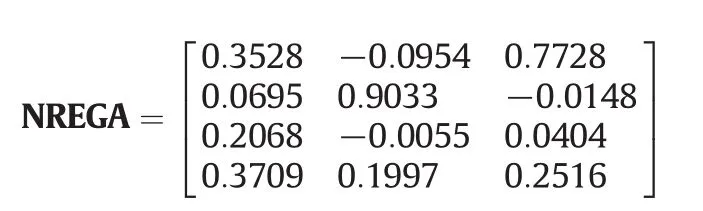
All sums of each row elements are calculated as 0.9802,0.9579,0.2417 and 0.8202.According to the squaring method,we remove the third output variable y3.We have the square subsystem

Table 1 Process transfer function matrix for distillation column

and calculate the REGA as

According to the pairing criterion based on REGA,we have the final pairing y1−u3,y2−u2and y4−u1forthis“thin”system.This pairing result is in accordance with the one in literature[17].

4.Closed-loop Evaluation for Control Con figuration Design

From the two examples in Section 3,some interaction analysis methods cannot provide appropriate variable pairing for all multivariable systems.Therefore,it is necessary to evaluate if the recommended pairing is proper.

How could we know if the pairing is proper or not for a closed-loop system?The control performance curve may provide the evidence.However,it cannot illustrate the extent of appropriateness or inappropriateness of recommended pairing accurately and intuitively.Therefore,some quantitative index for evaluating the recommended pairing is more preferred.

In this part,a closed-loop relative gain(CRG)is defined as the quantitative index,and whether the CRG is within specified scope determines the appropriateness or inappropriateness of recommended pairing[19].

For ij loop,the traditional relative gain between ujand yican be easily transformed into

In the definition of relative gain,the use of controllers with integral is inherent.It is sometimes referred to as the“perfect control requirement”.A better term would be “perfect steady-state control requirement”because the integral control leads to offset-free.When the steady-state output yiis approximately equal to its setpoint yi,sp,we can rewrite Eq.(15)to

where λ′ijis defined as CRG,which is the ratio of the gain between controller output ujand controller input yi,spwhen all other loops is closed to the gain between ujand yi,spwhen all other loops is open.

For ij loop,when all other loops is closed,the steady-state gain between controller output ujand controller input yi,spis defined as^kij,which can be obtained easily from experimental data.

When all other loops is closed and a step input is added to yi,sp,the energy consumption for manipulated variable ujrepresenting the process dynamics is defined as

where(∞)represents the final steady-state value of normalized input and(t)can be easily obtained from experimentaldata.Eq.(17)is similar to the one of Eq.(4)for REGA.A small energy consumption value implies a fast dynamic response for manipulated variable,whereas a large one indicates a slow process dynamic response.

With the steady-state gainand energy consumptionbetween yi,spand uj,the closed-loop dynamic gain of ij loop with all other loops closed can be obtained as

Similarly,for ij loop,when all other loops is open,the steady-state gain between controller output ujand controller input yi,spis defined asand the energy consumption for manipulated variable ujwith a step input added tois defined asthen the closed-loop dynamic gain of ij loop with all other loops open can be obtained as if ned in Eq.(16)can be derived as

Finally,the closed-loop dynamic relative gain(CDRG)of ij loop de-

For remaining n-1 control loops,the dynamic relative gain can also be obtained through Eqs.(18)–(20).

Based on the CDRG,we can give an evaluation criterion.

For ij control loop,if 0.7≤λ′ij≤1.2,this control loop is proper with tolerable interaction level.

If λ′ij≤ 0,the controlled loop will be unstable,so this pairing result is inappropriate.

If 0＜λ′ij＜ 0.7 or λ′ij＞ 1.2,there are large interactions from other loops,the recommended pairing is usually considered inappropriate.

If the CDRG of each closed-loop belongs to the scope,the recommended pairing is proper.Otherwise,the pairing is inappropriate and another one is needed.Generally,more than two control loops are not in the best scope with inappropriate pairing simultaneously.

We have the evaluation procedure as follows.

(1)Design the optimal PID controller through same approach for each control loop.

(2)Record sampled data of manipulated variables and steady-state gains between controller outputs and controller inputs with other control loops open or closed,and calculate the closedloop dynamic gains according to Eqs.(18)and(19).

(3)Calculate CDRGs for all control loops according to Eq.(20).

(4)Judge whether the CDRGs are in the best scope.If all the CDRGs are in the scope,the recommended pairing is proper for multivariable system.Otherwise,the pairing is inappropriate.Finding another one,and go to step(1).

Example 5.Consider a 3×3 system

The interaction analysis method based on ERGA is utilized for obtaining pairing.We have the ERGA for this system:

The system can be stable with both pairings(NI＞0)y1−u2,y2−u1,y3−u3(defined as P1)and y1−u1,y2−u3,y3−u2(defined as P2),and P1 is recommended according to the pairing criterion based on ERGA method.According to the evaluation procedure,we obtain the CDRGs for all control loops: λ′13=0.3778, λ′22=0.3026, λ′31=0.7663.Apparently, λ′13and λ′22exceed the best scope,so that the recommended pairing is inappropriate.With another pairing P2,following the evaluation procedure,the closedloop dynamic relative gains for all loops can be obtained:λ′13=0.7438,λ′22=0.7494,λ′31=0.7438.Apparently,all the dynamic relative gains are within the best scope,so this pairing is appropriate for this system.

The control performance of the controlled system with two pairing is shown in Fig.6.The control performance with pairing P1 recommended by ERGAis worse than the one with P2.ERGAdoes notmeasure the interactions accurately and provide appropriate pairing for this system.This may happen to other interaction measurement methods for many MIMO systems.On the other hand,the closed-loop evaluation method proposed in this paper is effective and can provide some credible evaluation for recommended pairing.

5.Conclusions

This paper focuses on interaction analysis approaches and pairing evaluation method originated and developed in our group,and demonstrates our concept and idea for control configuration design.There are three extinct contributions.

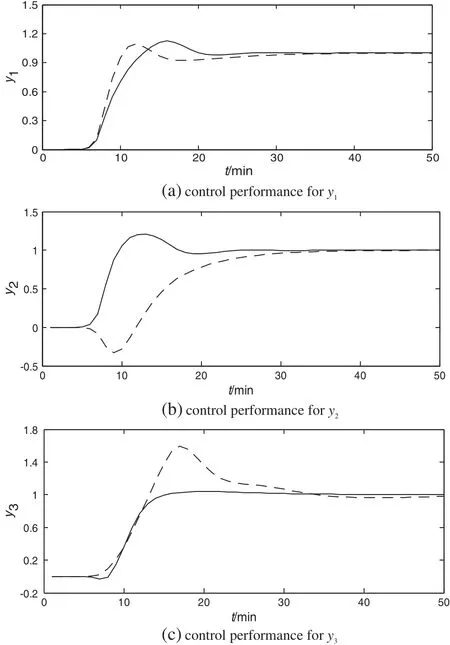
Fig.6.Control performance with two pairings.control performance with pairing P2;— —control performance with pairing P1.

(1)A new interaction analysis approach in open-loop introduces

new concept of control energy consumption,based on which the contributions of response time constant and delay time to dynamics of relative gain are rebalanced and more reasonable.(2)More detailed analysis about system types and main pairing problem for non-square systems is taken.The extension of one of the proposed open-loop pairing approaches is utilized for non-square system pairing.

(3)For examining whether a recommended pairing is proper,an evaluation method is proposed in closed-loop with optimal controllers foreach loop.The closed-loop relative gains between manipulated variables and controlled variables setpoints are presented as an evaluation index.When they are within a defined scope,one can determine if the pairing is appropriate.

Appendix A

When gij(s)is described as FOPDT model,we have

When gij(s)is described as SOPDT model,we have

Let

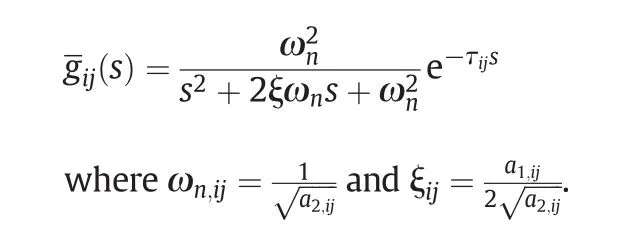
If 0＜ξij＜1,the normalized output is calculated as

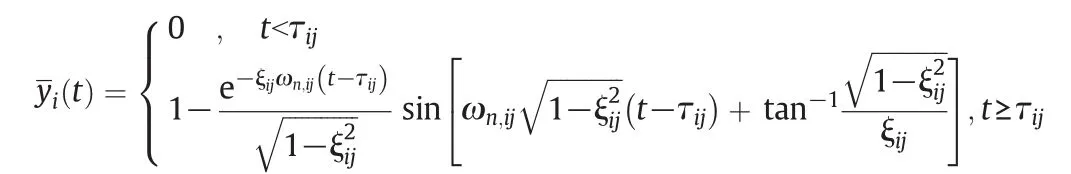
and

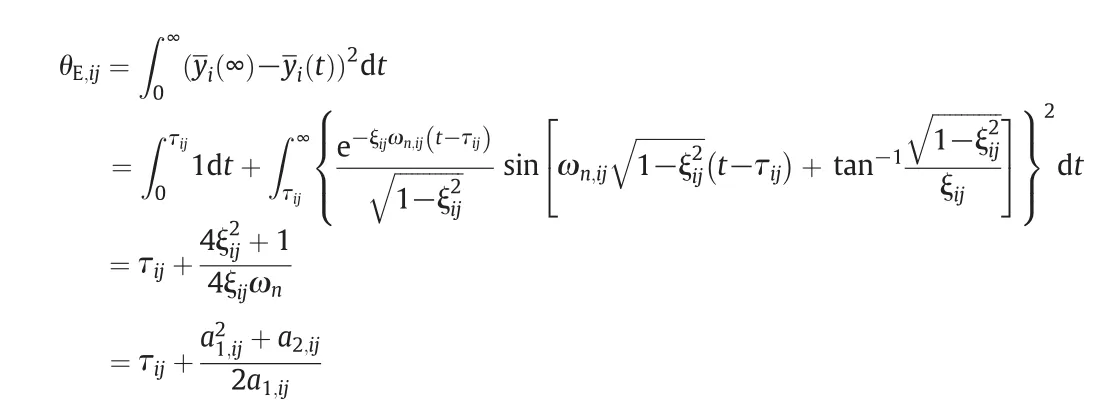
If 1＜ξij＜∞,(s)can be rewritten to

We have the roots of characteristics equation as

and

The normalized output is calculated as

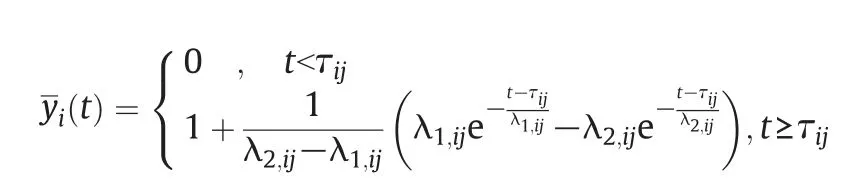
and

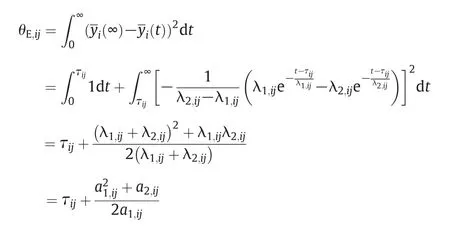
Therefore,if gij(s)is described as SOPDT model,we have the control energy consumption as

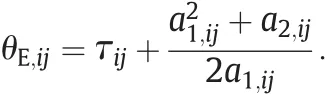
[1]E.Bristol,On a new measure of interaction for multivariable process control,IEEE Trans.Autom.Control 11(1)(1966)133–134.

[2]A.Niederlinski,A heuristic approach to the design of linear multivariable interacting control systems,Automatica 7(6)(1971)691–701.

[3]P.Grosdldler,M.Morari,B.R.Holt,Closed-loop properties from steady state gain information,Ind.Eng.Chem.Fundam.24(2)(1985)221–235.

[4]M.F.Witcher,T.J.McAvoy,Interaction control systems:steady state and dynamic measurement of interaction,ISA Trans.16(3)(1977)35–41.

[5]J.P.Gagnepain,D.E.Seborg,Analysis of process interactions with application to multiloop control system design,Ind.Eng.Chem.Process.Des.Dev.21(1)(1982)5–11.

[6]F.M.Meeuse,A.E.M.Huesman,Analyzing dynamic interaction of control loops in the time domain,Ind.Eng.Chem.Res.41(18)(2002)4585–4590.

[7]T.McAvoy,Y.Arkun,R.Chen,D.Robinson,P.D.Schnelle,A new approach to defining a dynamic relative gain,Control.Eng.Pract.11(8)(2003)907–914.

[8]Q.Xiong,W.J.Cai,M.J.He,A practical loop pairing criterion for multivariable processes,J.Process Control 15(7)(2005)741–747.

[9]Q.Xiong,W.J.Cai,M.J.He,Decentralized control system design for multivariable processes—a novel method based on effective relative gain array,Ind.Eng.Chem.Res.45(8)(2006)2769–2776.

[10]Q.Xiong,W.J.Cai,Effective transfer function method for decentralized control system design for multi-input multi-output processes,J.Process Control 16(8)(2006)773–784.

[11]Q.Xiong,W.J.Cai,M.J.He,Equivalent transfer function method for PI/PID controller design of MIMO processes,J.Process Control 17(8)(2007)665–673.

[12]M.J.He,W.J.Cai,W.Ni,L.H.Xie,RNGA based control system configuration for multivariable processes,J.Process Control 19(6)(2009)1036–1042.

[13]N.Monshizadeh-Naini,A.Fatehi,A.K.Sedigh,Input–output pairing using effective relative energy array,Ind.Eng.Chem.Res.48(15)(2009)7137–7144.

[14]M.Morari,G.Stephanopoulos,Studies in the synthesis of control structures for chemical processes:part III:optimal selection of secondary measurements within the framework of state estimation in the presence of persistent unknown disturbances,AICHE J.26(2)(1980)247–260.

[15]S.Treiber,Multivariable control for non-square systems,Ind.Eng.Chem.Process.Des.Dev.23(4)(1984)854–857.

[16]M.Morari,W.Grimm,M.J.Oglesby,I.D.Prosser,Design of resilient processing plants—VII.Design of energy management system for unstable reactors—new insights,Chem.Eng.Sci.40(2)(1985)187–198.

[17]J.W.Chang,C.C.Yu,The relative gain for non-square multivariable systems,Chem.Eng.Sci.45(5)(1990)1309–1323.

[18]D.E.Reeves,Y.Arkun,Interaction measure for nonsquare decentralized control structures,AICHE J.35(4)(1989)603–613.

[19]X.L.Luo,L.H.Ren,P.F.Cao,Y.Zhao,F.Xu,A closed-loop evaluation for regulatory control structure of multivariable system,Proceedings of the 10th World Congress on Intelligent Control and Automation,2012.

[20]M.J.He,W.J.Cai,B.F.Wu,M.He,Simple decentralized PID controller design method based on dynamic relative interaction analysis,Ind.Eng.Chem.Res.44(22)(2005)8334–8344.