Orthogonal nonnegative matrix factorization based local hidden Markov model for multimode process monitoring☆

Fan Wang,Honglin Zhu,Shuai Tan,Hongbo Shi*

Key Laboratory of Advanced Control and Optimization for Chemical Processes of Ministry of Education,East China University of Science and Technology,Shanghai 200237,China

1.Introduction

Fault detection is one of the most important tasks for successful operation of chemical processes.Multivariate statistical process monitoring(MSPM)is growing popular due to large amount of data from large-scale chemical processes.MSPM techniques,such as principal component analysis(PCA)and partial least-squares(PLS),have been intensively investigated and widely applied to chemical process monitoring with success[1–3].To overcome the limitations,such as nonlinearity and dynamics of processes,improvements on traditional methods and other complementary MSPM have been proposed,such as ICA,KPCA,DPCA,SVDD and manifold-learning methods[4–9].However,it should be noted that these approaches often assume that the process operates in a single mode,while complex chemical manufacturing processes often work in multiple modes.Consequently,mode shifts greatly confine the scope of applications of conventional techniques.

For monitor processes with multiple operating modes,Chen and Liu[10]proposed a mixture principal component analysis model detector,which is a group of PCA models.Zhao et al.[11,12]handled the processes with multiple PCA models and multiple PLS models.These approaches constructed multiple models for different operating modes to carry out the monitoring task.Based on this idea,Liu[13],Yoo et al.[14],Ng and Srinivasan[15],Khediri et al.[16]and Zhu et al.[17]came up with other techniques.Yu and Qin[18]developed a finite Gaussian mixture model and used the Bayesian inference-based probability index for process monitoring.Ge and Song[19]presented a mixture Bayesian regularization method of PPCA.These methods integrated monitoring results of different operating modes in a probabilistic manner.

In contrast to above traditional approaches,hidden Markov model(HMM)-based methods have not been explored widely and deeply in multimode process monitoring.Yu[20]applied HMM to model complicated data distribution with nonlinear and multimodal features and developed two HMM-based process monitoring quantification indications.Rashid and Yu[21]presented a HMM based ICA approach for processes with multiple operating modes and inherent system uncertainty.The hidden Markov model was built to estimate dynamic mode sequence.Then the local ICA models were developed to characterize differentoperating modes for online process monitoring purpose.Ning etal.[22]incorporated HMMand the window-based SPA monitoring method in a single framework where HMM is adopted to identify the operating mode.

In this paper,a novel process monitoring scheme based on HMM is proposed for multimode processes.First,a new clustering method named orthogonal nonnegative matrix factorization(ONMF)is used to divide data of different modes.Then,multiple local HMMs are constructed for various operating modes.Because hidden Markov model is a powerfultool to describe a stochastic sequence,the proposed method does not presume the distribution of sample data in each operating mode.Furthermore,build a HMMfor every mode with higher modeling accuracy.During online monitoring period,the monitored samples can be classified into proper modes by comparing the relevance with every HMM.At last,the HMM based monitoring indication named negative log likelihood probability(NLLP)is used for fault detection in every mode.The effectiveness ofthe proposed approach is shown by a numerical example and the Tennessee Eastman(TE)process.

2.Method

2.1.Orthogonal nonnegative matrix factorization

Orthogonal nonnegative matrix factorization(ONMF)works well for clustering tasks in document clustering field and is equivalent to K-meansclustering in the sense thatthey share the same objective function[23,24].ONMF can be viewed as approximate matrix factorization techniques with both nonnegative and orthogonal constraints,which is formulated as the following optimization problem:

subject to W≥0,H≥0,HHΤ=I

where X⊂Rm×n,W⊂Rm×k,H⊂Rk×n,and the entries of matrices X,W and H are nonnegative.

The factor matrices W and H have the following explanation.When columns of original data matrix X are data points in m dimensional space,columns in W are treated as basis vectors and every row in H represents encoding that means the extent to which each basis vector is utilized to reconstruct original data vector.

2.2.Hidden Markov model

Hidden Markov model(HMM)is a probabilistic model extended from Markov chains to generate the statistically inferential information on a series of state sequences[25].In general,it contains finite numbers of hidden states,where each state outputs an observation at certain time point.Each hidden state is characterized by two sets of probabilities:a transition probability between two states and an observation probability distribution.Not like Markov chains,HMM are doubly stochastic processes:the stochastic transition between one state to another state and stochastic output observations generated at each state.A HMM has the following key ingredients[25].

(1)The hidden states

where N denotes the number of hidden states.

(2)State transition probability distribution

where aij=Pr(qt+1=Sj|qt=Si),1≤i,j≤N,and qtis the hidden state at time t.

(3)The observations

where M represents the number of distinctive observation per state.M is in finite when the observation space is continuous.

(4)The observation probability distribution

where bi(K)=Pr(OK|qt=Si),1≤i≤N,1≤K≤M.

(5)Initial hidden state probability distribution

where πi=Pr(qt=1=Si),1 ≤ i≤ N.

The three main components of a HMM are the state transition probability matrix A,the measurementprobability distribution matrix B,and the initial state probability distribution π.For convenience,a compact notation is used to indicate the complete parameter set of the model:

In a HMM,the following three basic problems need to be solved:training parameters of HMMs,calculating the probability of one observation sequence,and finding a state sequence that matches the observation sequence perfectly.There are three basic algorithms,namely the Baum–Welch algorithm,the forward–backward procedure and the Viterbi algorithm[25].

3.ONMF Based Local HMM for Multimode Processes Monitoring

For multimode process fault detection,this work implements a monitoring procedure based on local HMM models.This method is applied by combining the ONMF clustering algorithmand HMMalgorithm introduced in the preceding section.To design the monitoring scheme,the dataset is first separated using ONMF clustering approach.This allows us to divide different groups of datasets with similar characteristics.Then,for each class of data a local HMM is constructed to describe the underlying data distribution.At last,the new observation samples are monitored by determining their proper mode label and then computing the monitoring indicator in the correct HMM model.

3.1.Of fline modeling

When ONMF is applied to clustering,dimension k refers to the number of clusters.Let each column of the data set Y(J×T)(where J is the number of variables and T is the sample number)be treated as a data sample,then after the factorization,each column of W(J×k)represents a cluster center and elements of every column of H(k×T)are the cluster indicator.

After the clustering task,multiple local HMMs are constructed for different modes.

3.2.Local HMM for mode identification and fault detection

In a HMM,negative log likelihood probability(NLLP)presents how well a new observed data sample matches the probability distribution of HMM trained by a data set.Thus it can be employed for both mode identification and fault detection.After local HMM models are built for each mode,a data sample must have minimal NLLP in the local HMM,which corresponds to the mode it belongs to.For fault detection,when the data sample is normal,the NLLP is small since it follows the HMM distribution perfectly.On the other hand,the NLLP of a fault data sample should be larger than usual one.Therefore,NLLP can act as an effective monitoring index for evaluating process states.

This quantization indication is developed by calculating the probability P(yt∣λ)of one observation sample yt,given the HMM model λ.This mathematical problem can be solved by the forward–backward procedure.

For a data set Y(J×T)=[y1,y2,…,yT],define a forward variableαt(i),which is the probability of the partial observation sequence(until time t),and state Siat time t,given the model λ.

We can solve αt(i)by inductive steps as follows.

where 1≤i≤N.

where 1≤t≤T−1 and 1≤j≤N.

As a result,NLLP is computed as

During online process monitoring stage,compute NLLP of the monitored sample in every local HMM.Then the sample can be located in the proper HMM with the minimal NLLP.At last,compare its NLLP against the threshold in the local model to determine whether this data sample is normal or not.

3.3.The proposed monitoring procedure

The monitoring procedure based on the proposed method includes two stages:of fline modeling and online process monitoring.The procedure is summarized as follows.

Of fline modeling:

(1)Collect data samples when the process is under normal condition.The pre-processing of dataset is implemented.

(2)Use ONMF for the clustering job.

(3)Build local HMM models for each mode and utilize the Baum–Welch algorithm to obtain the parameters of HMM,namely λ=(A,B,π).

(4)Calculate the NLLP of normal samples in every local HMM and determine corresponding threshold for NLLP by the KDE method with a confidence bound.

Online process monitoring:

(1)For every monitored data sample,compute NLLP in every HMM and determine proper local HMM with minimal NLLP.

(2)Locate the sample in suitable HMM,and compare its NLLP against the threshold of local HMM to decide whether it is normal or not.

4.Illustrative Examples

4.1.A numerical example

A multivariate linear system is first used to demonstrate the effectiveness of the proposed method,and its performance is compared with the kernel K-means clustering based local SVDD method[16].The simulation process is a three variable multimodalprocess,originally suggested by Yu and Qin[18].

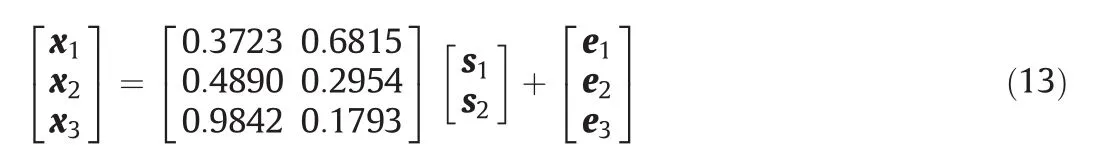
where[s1,s2]Τdenotes Gaussian distribution data sources and[e1,e2,e3]Τare zero-mean white noises with standard deviations of 0.01.Three operating modes and corresponding data sources are listed as follows.

For each operating mode,100 samples are generated and total 300 samples are used as training data.

To show the performance of the proposed monitoring method,the test data are generated in the following two faulty situations.

Case 1:the system is initially running at mode 1,and then a bias error of 4 is added to x1from the 101st through 200th samples.

Case 1:the system is initially running at mode 2,and a drifting error of 0.04(l-100)with l denoting the serial number of test samples is applied to x2between the 101st through 200th samples.

In this numerical simulation,300 normal data samples from three operating modes are collected for of fline modeling training.The confidence level is chosen as 98%for both approaches so that the proposed method can be compared with its counterparts fairly.

In Case 1,measurement x1is contaminated by a bias fault of some magnitude in 101–200 samples.Fig.1 shows that the K-means based SVDD method fails to provide a satisfactory monitoring consequence due to its miss fault detection performance.In contrast,as shown in Fig.2,NLLP detects all faults from samples 100–200 while they hardly trigger false alarms for the normal observation from samples 1–100.

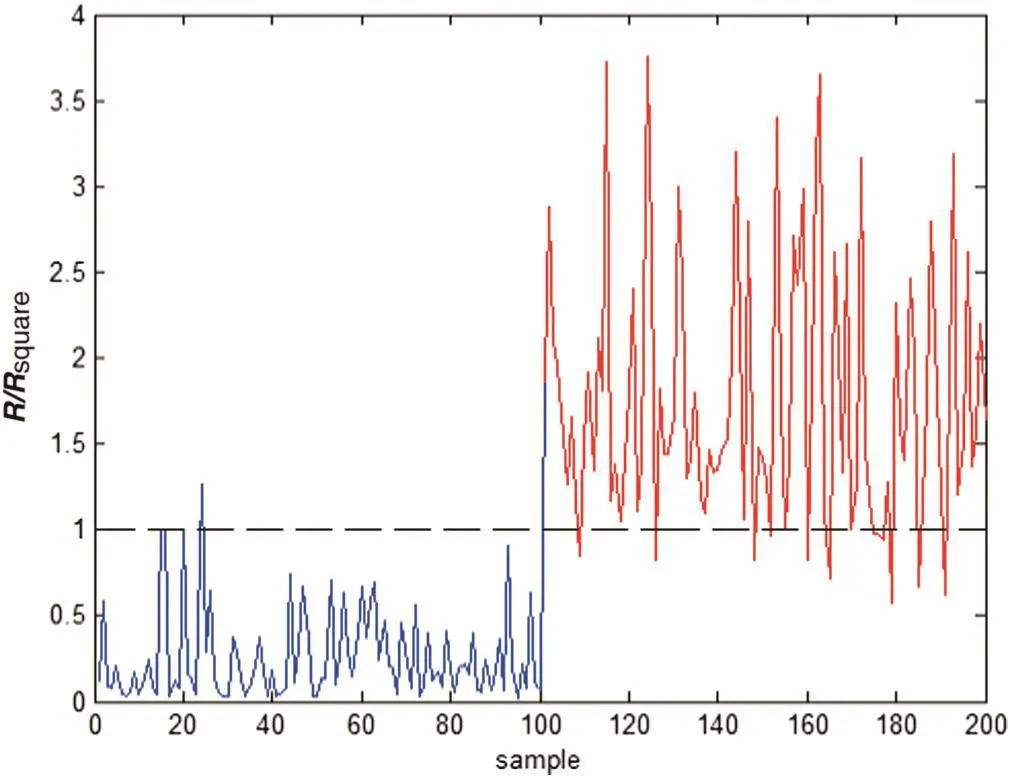
Fig.1.Monitoring results of kernel K-means based local SVDD for Case 1.

In Case 2,the capability of detecting a drift fault is tested with two monitoring approaches.Fig.3 depicts the monitoring results of the K-means clustering based local SVDD method.The drift fault can only be well captured until the 140th sample.It means that operators catch the fault with a time lag of about 40 samples.As a comparison,the monitoring performance is improved by utilizing our proposed method according to Fig.4.It is able to detect the drift fault with a delay of about 30 samples.

4.2.The Tennessee Eastman process

The ONMF based local HMM monitoring method is applied to the Tennessee Eastman(TE)process developed by Down and Vogel[26].The process consists of five major unit operations:a reactor,a product condenser,a vapor–liquid separator,a recycle compressor,and a product stripper.Overall 41 measured output variables and 12 manipulated variables are involved in this process.The decentralized control scheme developed by Richer is employed to generate closed-loop data[27].

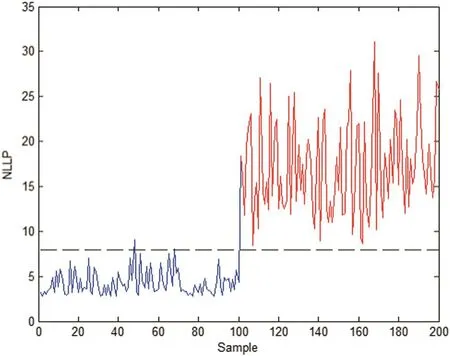
Fig.2.Monitoring results of ONMF based local HMM for Case 1.

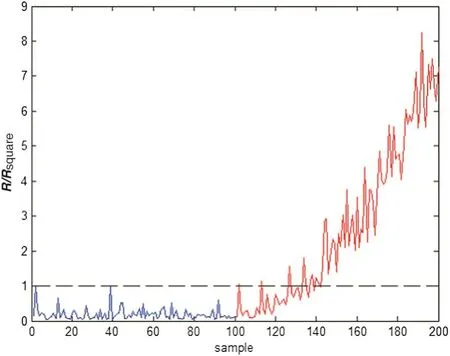
Fig.3.Monitoring results of kernel K-means based local SVDD for Case 2.

Fig.4.Monitoring results of ONMF based local HMM for Case 2.

In this paper,modes 1 and 3 are adopted to evaluate the effectiveness of the proposed method.Total 60 h normal data samples are collected from each mode as the training data.The sampling time interval is 0.03 h.A total of 31 variables,which contains 22 continuous process measurements and 9 manipulated variables,are utilized to conduct process monitoring.

First,the training data samples of modes 1 and 3 are separated by ONMF.Dimension k is chosen as 2 because the number of clusters is 2.After the calculation,the matrix W has the meaning of cluster centroids so the two columns(w1and w2)of W represent two clustering centers.Then the matrix H acts as the cluster indicator.The clustering results are presented in Fig.5.The red dots mean data samples of mode 1 while blue ones are those from mode 3.It is clear that ONMF has the ability to do clustering job well.

Fig.5.Clustering results of data samples from modes 1 and 3.

The monitoring results of the ONMF based local HMM method are compared to those of the kernel K-means clustering based local SVDD approach[16].The same training data set is selected for both methods.The thresholds of monitoring indices are obtained under 99%con fidence level to guarantee a fair comparison.In the online monitoring part,14 different faults of two modes are all tested.The test data set includes 1000 data samples where the first 200 samples are normal ones and process faults are introduced from the 201st sample to the end.The fault detection results of the two approaches are listed in Table 1.It isobvious that our proposed method has higher fault detection rates in most cases.For example,for fault 4,the fault detection rate of kernel K-means based local SVDD is 1.375%,while that of ONMF based local HMM is 100%.The monitoring results of the proposed approach for faults 10 and 11 are also much better.Table 2 gives similar results.The proposed method is quite successful in detecting faults 4 and 11.

Table 1 Monitoring results of 14 faults in TE mode 1

Table 2 Monitoring results of 14 faults in TE mode 3

5.Conclusions

A novel monitoring approach combining ONMF clustering and hidden Markov model(HMM)is developed for multimode processes.For complex chemicalprocesses with multiple operating modes and system uncertainty,the proposed method employs ONMF to classify data samples of diverse modes.The process uncertainty and dynamics can be well interpreted through the hidden Markov estimation.Then the quantification indication NLLP is responsible for fault detection.The case studies on a numerical example and the TE process show that the proposed method can effectively deal with multimode process monitoring problem.Since a transition stage always exists in various operating modes in actual processes,transitional modes will be the future research direction.

[1]S.J.Qin,Statistical process monitoring:Basics and beyond,J.Chemom.17(2003)480–502.

[2]M.Kano,K.Nagao,S.Hasebe,I.Hashimoto,H.Ohno,A new multivariate statistical process monitoring method using principal component analysis,Comput.Chem.Eng.25(2001)1103–1113.

[3]X.Wang,U.Kruger,B.Lennox,Recursive partial least squares algorithms for monitoring complex industrial processes,Control.Eng.Pract.11(2003)613–632.

[4]M.Kano,K.Nagao,S.Hasebe,I.Hashimoto,H.Ohno,Monitoring independent components for fault detection,AICHE J.49(2003)969–976.

[5]C.Y.Cheng,C.C.Hsu,M.C.Chen,Adaptive kernel principal component analysis(KPCA)for monitoring small disturbances of nonlinear processes,Ind.Eng.Chem.Res.49(2010)2254–2262.

[6]Y.X.Ma,B.Song,H.B.Shi,Y.W.Yang,Neighborhood based global coordination for multimode process monitoring,Chemom.Intell.Lab.Syst.139(2014)84–96.

[7]X.Q.Liu,K.Li,M.McAfee,G.W.Irwin,Improved nonlinear PCA for process monitoring using support vector data description,J.Process Control 21(2011)1306–1317.

[8]B.Song,Y.X.Ma,H.B.Shi,Multimode process monitoring using improved dynamic neighborhood preserving embedding,Chemom.Intell.Lab.Syst.135(2014)17–30.

[9]Z.Q.Ge,Z.H.Song,Process monitoring based on independent component analysis–principal component analysis(ICA–PCA)and similarity factors,Ind.Eng.Chem.Res.46(2007)2054–2063.

[10]J.H.Chen,J.L.Liu,Mixture principal componentanalysis models for process monitoring,Ind.Eng.Chem.Res.38(1999)1478–1488.

[11]S.J.Zhao,J.Zhang,Y.M.Xu,Monitoring of processes with multiple operating modes through multiple principle component analysis models,Ind.Eng.Chem.Res.43(2004)7025–7035.

[12]S.J.Zhao,J.Zhang,Y.M.Xu,Performance monitoring of processes with multiple operating modes through multiple PLS models,J.Process Control 16(2006)763–772.

[13]J.L.Liu,Process monitoring using Bayesian classification on PCA subspace,Ind.Eng.Chem.Res.43(2004)7815–7825.

[14]C.K.Yoo,K.Villez,I.B.Lee,C.Rosen,P.A.Vanrolleghem,Multi-model statistical process monitoring and diagnosis of a sequencing batch reactor,Biotechnol.Bioeng.96(2007)687–701.

[15]Y.S.Ng,R.Srinivasan,An adjoined multi-model approach for monitoring batch and transient operations,Comput.Chem.Eng.33(2009)887–902.

[16]L.B.Khediri,C.Weihs,M.Limam,Kernel k-means clustering based local support vector domain description fault detection of multimodal processes,Expert Syst.Appl.39(2012)2166–2171.

[17]Z.B.Zhu,Z.H.Song,A.Palazoglu,Process pattern construction and multi-mode monitoring,J.Process Control 22(2012)247–262.

[18]J.Yu,S.J.Qin,Multimode process monitoring with Bayesian inference-based finite Gaussian mixture models,AICHE J.54(2008)1811–1829.

[19]Z.Q.Ge,Z.H.Song,Mixture Bayesian regularization method of PPCA for multimode process monitoring,AICHE J.56(2010)2838–2849.

[20]J.B.Yu,Hidden Markov models combining local and global information for nonlinear and multimodal process monitoring,J.Process Control 20(2010)344–359.

[21]M.M.Rashid,J.Yu,Hidden Markov model based adaptive independent component analysis approach for complex chemical process monitoring and fault detection,Ind.Eng.Chem.Res.51(2012)5506–5514.

[22]C.Ning,M.Y.Chen,D.H.Zhou,Hidden Markov model-based statistics pattern analysis for multimode process monitoring:an index-switching scheme,Ind.Eng.Chem.Res.53(2014)11084–11095.

[23]J.Yoo,S.Choi,Orthogonal nonnegative matrix tri-factorization for co-clustering:Multiplicative updates on Stiefel manifolds,Inf.Process.Manag.46(2010)559–570.

[24]F.Pompili,N.Gillis,P.A.Absil,F.Glineur,Two algorithms for orthogonal nonnegative matrix factorization with application to clustering,Neurocomputing 141(2014)15–25.

[25]L.R.Rabiner,A tutorial on hidden Markov models and selected applications in speech recognition,Proc.IEEE 77(1989)257–286.

[26]J.J.Down,E.F.Vogel,A plant-wide industrial process control problem,Comput.Chem.Eng.17(1993)245–255.

[27]N.L.Richer,Decentralized control of the Tennessee Eastman challenge process,J.Process Control 6(1996)205–221.