音阶的另类计算法
戴念祖
(中国科学院 自然科学史研究所,北京 100190)
·乐律学·
音阶的另类计算法
戴念祖
(中国科学院 自然科学史研究所,北京 100190)
摘要:文章对五度律(三分损益律)、纯律、平均律和等程律等,提出一种简捷、实用的计算方法, 可供音乐史和科学史的教学和研究参考,也有助音乐院校学生的学习和拓展思维。
关键词:音程;五度律;纯律;琉特琴(lute)律;平均律;等程律;计算
音阶的数学计算,是科学史(物理学史)、音乐史(音乐基础理论)和乐律史必修的课程。近年来,或有人以为它是过时了的音乐学,或以为它是与乐音无关的高深知识。因涉及数学计算,它往往被人所忽略或望而却步。实际上,音阶的数学计算是音乐学的基础理论,正是它的进步才有音乐学的发展。音乐学的创新也少不了音阶知识的基础。本文不揣冒昧,提出一种或许较为简捷、实用、且易记忆的计算方法。或许有助相关学科的教学和研究、增添某些新知。不当之处,祈识者正之。
一、音程计算法
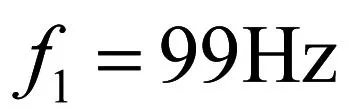
假定两个乐音的频率分别为f1、f2,其音程△则为

(2)式是音程表述的普遍形式。
大家知道,有一个对数换底公式。即以α为底的对数可以换成以b为底的对数。设真数为M,则换底公式为
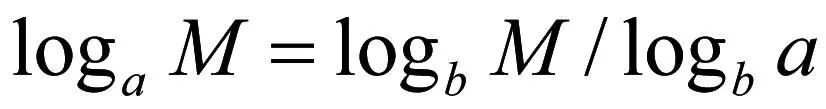
按照(3)式,可将(2)式中以β为底的对数换成以10为底的对数,即
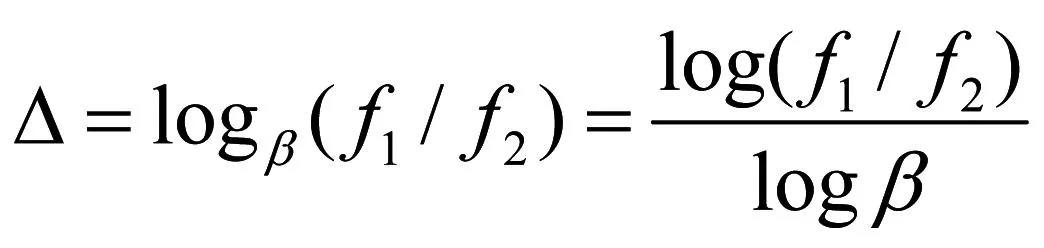
将(1)式的β值代入(4)式,
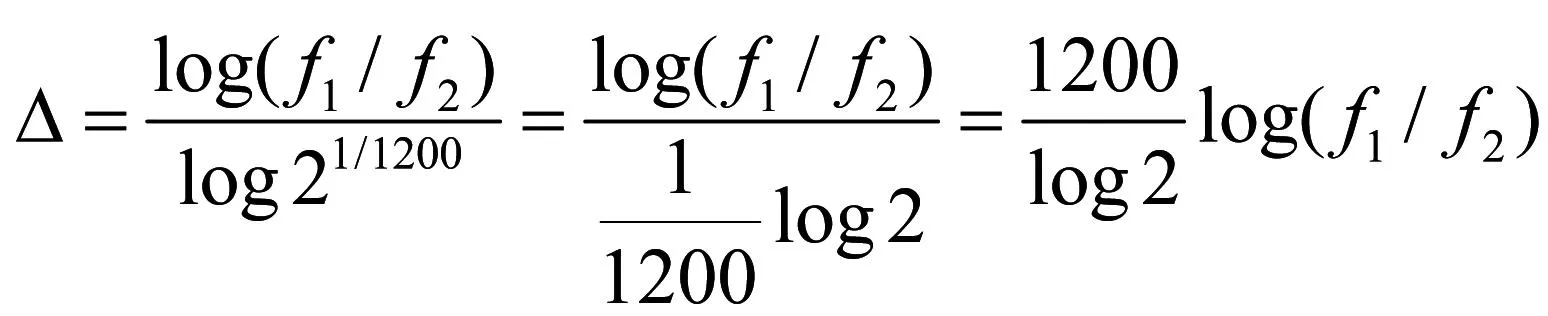
查对数表,log2=0.30103,代入(5)式作运算。因此,

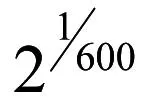
知道以上数学含义,音程计算可以简化为:
假定倍频程对数值为1200音分,即假定log2=1200,则任一音程△的音分值与之成比例,即

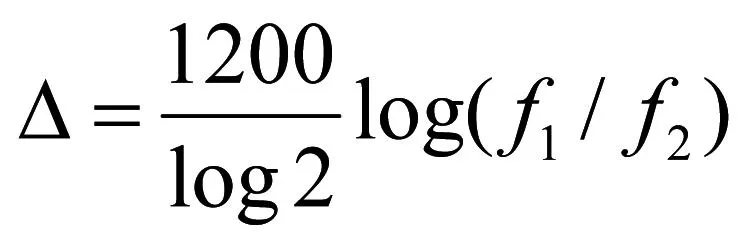
(7)式和(5)式完全相同。
二、五度律音阶的计算
五度律(fifth temperament)或五度音阶(fifth scale)的计算是律学计算的基础。它的计算方法是大家所熟悉的,其相生因子为3/2(频率比,其倒数则为弦长比)。我们仅作一简单叙述。
设C=1,计算步骤如下:
(1)由C上生得G、D、A、E、B;
(2)由B上生得#F、#C、#G、#D、#A;
(3)由起始律C下生五度得F(这是五度律计算中关键的一步!);
(4)由F下生得bB、bE、bA、bD、bG。
完成上述四步,五度音阶即计算完成。具体计算如下。以下计算中右边的数值为按上述音程计算方法所得的对应乐律的音分值。
1)由C上生G开始计算:
C=1 0(音分)
G=3/2702
D=G×3/2÷2=9/8204
A=D×3/2=9/8×3/2=27/16906
E=A×3/2÷2=81/64408
B=E×3/2=243/1281110
2)由B上生#F开始计算:
#F=B×3/2÷2=243/128×3/2÷2 =729/512612
#C=#F×3/2÷2 =729/512×3/4=2187/2048114
#G=#C×3/2=2187/2048×3/2=6561/4096816
#D=#G×3/2÷2=6561/4096×3/4=19683/16384318
#A=#D×3/2=19683/16384×3/2=59049/1000
3)由C下生五度得
F=C×(3/2)-1×2=4/3498
4)由F下生bB始算;
Bb=F×(3/2)-1×2=16/9996
bE=bB×(3/2)-1=32/27294
bA=bE×(3/2)-1×2=128/81792
bD=bA×(3/2)-1=256/24390
bG=bd×(3/2)-1×2==1024/729588
将以上计算结果制成如下表1。该表左边按升半音划分音级,右边按降半音划分音级。其中,五度音阶的规律性一目了然。如,bD不等于#C,二者相差24音分,相当于一个古代音差(即毕达哥拉斯音差)值。
表1五度律音阶(单位:音分)

三、纯律大小音阶的计算
纯律(Just Intonation)或自然音阶(Natural Scale),其C大调的大小音阶有一个简捷公式,可供记忆。
设大全音为M,小全音为m,纯律大半音为s,已知:
M=9/8,
m=10/9,
S=16/15。
则,以这三个字母表示C大调纯律大、小音阶的公式如表2。
表2大调纯律大小音阶构成公式


特别要指出,这个表供读者比较纯律大小音阶的构成方式和规律,若以其表示音高,这两种音阶中的某些阶名则有别。按照表2中的各音级公式做具体运算后,不难发现:就音高而言,纯律大音阶的E、A、B比纯律小音阶的相同音级要高70音分。纯律小音阶的这三个音级比五度律低92音分,它们之间相差几近半音了。所以,对纯律小音阶而言,这三个音级应当记为bE、bA、bB;若以五度律为标准计,这三个音级更接近#D、#G、#A(参见表1)。
以上叙述表明,由表2可进而确定各音级的音高。有个别音乐家往往忽视物理过程,只追求音高的具体数值。他们对于某律制下的音级高低、甚至音分数背得滚瓜烂熟,而对这一数值的原始由来不予问津。记得在一次全国性律学讨论会上,笔者曾将表2讲述一番。自以为在繁杂的纯律计算中发现了一个简明可记忆的公式。不料,一个其时甚有名气的音乐理论家当即反对,其理由是该表错误地表述了纯律大小音阶的音高值。这才使我深深体会到,在物理学与音乐学之间进行交流沟通并非是一件容易的事。*表2中,纯律大音阶的公式化表述最先是由美国工程院院士、电讯专家戴振铎先生提出的[2]。戴振铎将其论文初稿寄我,我们曾作过有意义的讨论。在他工作基础上,我作了纯律小音阶的公式化表述,并获得戴振铎先生的肯定。特此申明,不敢掠美。戴振铎是江苏苏州人,我是福建长汀人,由于这些学术来往,才令彼此知晓。我们不仅同姓,且是同宗同族。我们都是戴氏谯国堂的子孙。戴振铎1937年清华大学物理系毕业,是叶企孙学生;我是1964年叶企孙的最后一个学生,甚至在叶先生被软禁的文革中,还受惠于叶先生指教。这是中国物理学史上的一个故事。
四、平均律和琉特琴律
平均律(mean tone temperament,有人称其“中庸律”),只流行于17-18世纪期间,随后被十二等程律(twelve tone equal temperament)所代替。关于它的计算方法,笔者在“消亡了的平均律”[3]一文中已作了讨论,此不赘。
琉特琴(lute)流行于14-17世纪的欧洲拨弦乐器。琉特律是16-17世纪期间为lute琴采用的调律方法。它是由意大利音乐家伽利莱(Vincenzo Galilei,约1520-1591)提出的。伽利莱是近代科学创始人、物理学家伽利略(Galilei Galileo,1564-1642)的父亲。伽利莱向当时著名音乐理论家、作曲家查利诺(G·Zarlino,1517-1590)学习音乐和作曲。后来,伽利莱成为颇具声望的琉特琴手和作曲家。但他和他的社团(佛罗伦萨集社)强烈反对他们老师查利诺提出的多声部以及和声的理论。伽利莱提出,半音的音程比率为18:17,并以此对琉特琴调律:
18/17-1.05882353,相当于半音为99音分。
表3琉特琴律

以18/17的比率调琉特琴律的结果如表3。与五度律相比较,琉特律的音阶结构中无升半音音程。由表1可见,五度律升半音为114音分。可见它与五度律相差较大。但它却与等程律近似,它与等程律的最大音差在c1上,为11音分。所以,琉特琴律是一种特殊的律制,它既非五度律,也非等程律。在拨弦乐器中,琉特律很适用于类似古希腊的单音音乐,是其时最富古典正统之美、又能满足那个时代之需要,且令人满意的调律。[4]但转调甚为免强且有限,和声几无可能。因此,这种律制在当时查利诺的多声部与和声理论中不可能得到运用。但它为西方音乐理论家走向十二等程律开拓了思维线路。
五、等程律
十二等程律(twelve tone equal temperament,本文常将其简称为等程律)是由明代音乐家、数学家朱载堉(1536-1611)创建的,朱载堉称数字为“密率”,他定义等程律(朱载堉称它为“新法密律”)为:
置一尺为实,以密率除之,凡十二遍。[5]
《新物理学词典》定义为:
等程律的半音音阶在一个八度中有十三律,任何相邻两律的音程是。[6]
《新格罗夫音乐和音乐家词典》定义为:
这个最简单的方法是要为半音选择一个正确的比例,然后把它运用十二次。[7]
朱载堉对等程律的定义和《新物理学词典》完全一致,而前者是在后者之前近400年作出的。上述三个定义都表明,十二等程律是以为公比数的一个等比数列。
在中国学术界流行将“等程律”称为“平均律”。其理由是:“平均律”的八度为1200音分,将此除以12,则每律为100音分。这是对“等程律”的误解。按照这些错误说法,朱载堉创建等程律的艰苦实在是徒劳且无智之举。
关于等程律计算,可参见笔者《从传统音乐学和数学角度看朱载堉创立等程律的思维》*发表于《中国音乐学》2014年第4期。一文。在此,本文以现代的科学和音乐学概念再作一次简单介绍,并对几种计算方法作出完整的计算。
表4等程律的第一种计算法


由表4可知,#C=bD,所有升半音都等于高一律的降半音。这才是等程律区别于其他律制的本质特点。但它并非是“平均1200音分”或“平均600音分”而轻易得到的。

表5中,纵实线为等比中项解,纵虚线为四项构成的等比数列的第二项,点线为四项中的第三项。就是说,#F是CC1的等比中项,#D和A分别为C#F、#FC1的等比中项;而#C、E、G、B分别为C#D、#D#F、#FA、AC1的第二项,其余(即点虚线者)为相应的第三项。计算步骤按表5中横栏从上到下进行。这也可以完成十二等程律音阶中各个音级的计算。它也是由明代音乐家朱载堉最早发现和计算的。
如同前二种解法一样,以下第三种解法又是朱载堉最早做出来的。它的意义是,如同五度律生律法一样,十二等程律也可以五度相生,甚至还可以四度相生,等等。只要如同五度律(其相生因子为3/2)一样,找出等程律的五度相生因子,问题就解决了。
表5等程律的第二种计算法
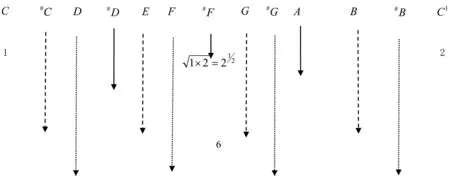

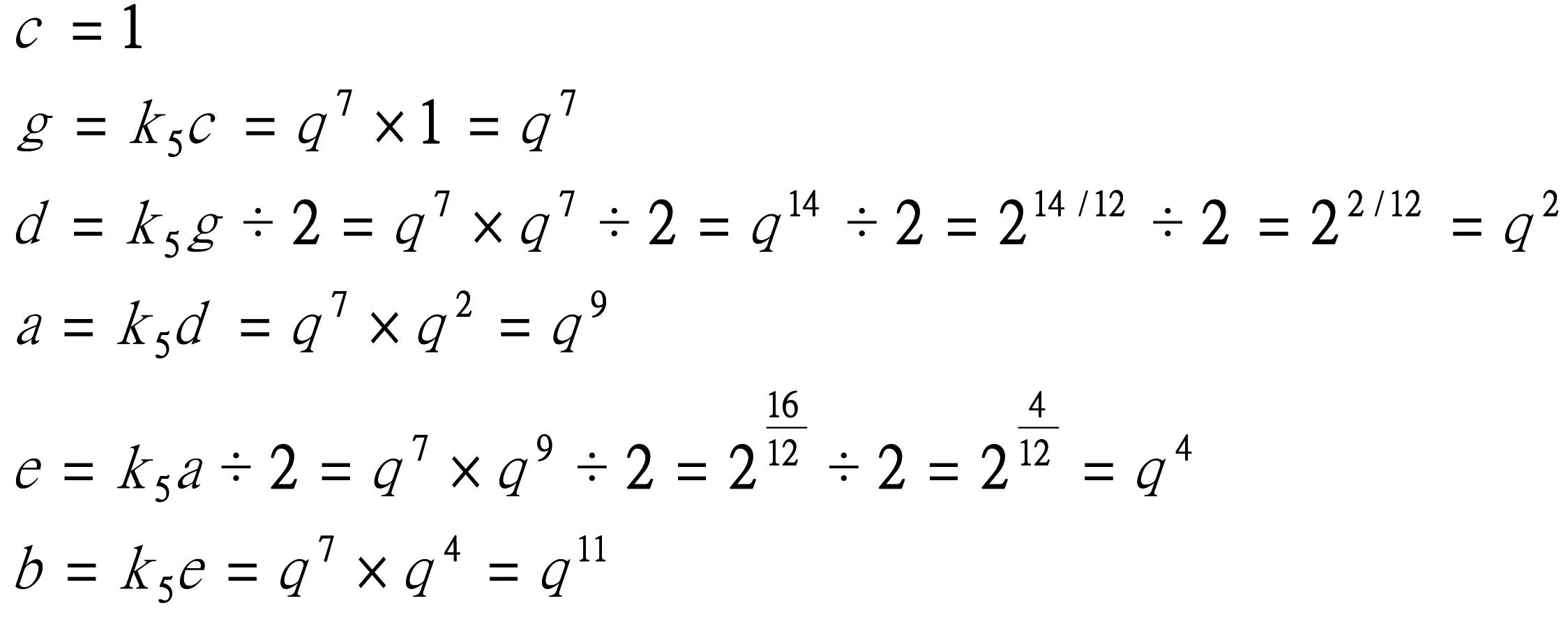
再从b上生#f开始计算,可得#c、#g、#d、#a,又从c1下生五度得f,一直到十二律算全。除了比列因子外,其计算方法与五度律完全相同。

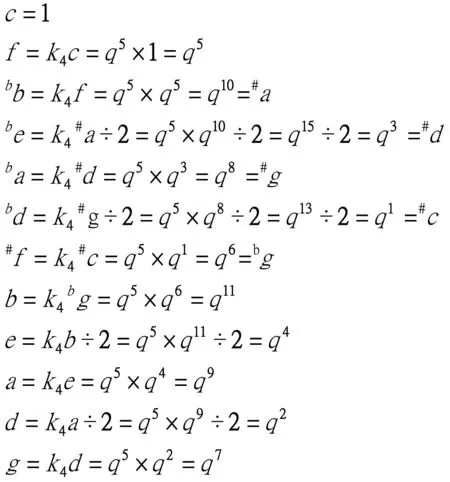
四度相生的十二等程律至此计算完毕。在此特别要指出,五度律是不可能从它的四度中产生的。这是等程律和五度律的根本不同之处。
如在表4中取上一横列数据以求k5,k4,其方法也相同,只要认清音级及其对应的频比数即可。如此,

要注意的是,相生因子k5、k4都是按照频率计算的。如果照弦长比数计算,就会得出和朱载堉相同的结果。我们将具体数值代入k5、k4中做一次计算就明白了。
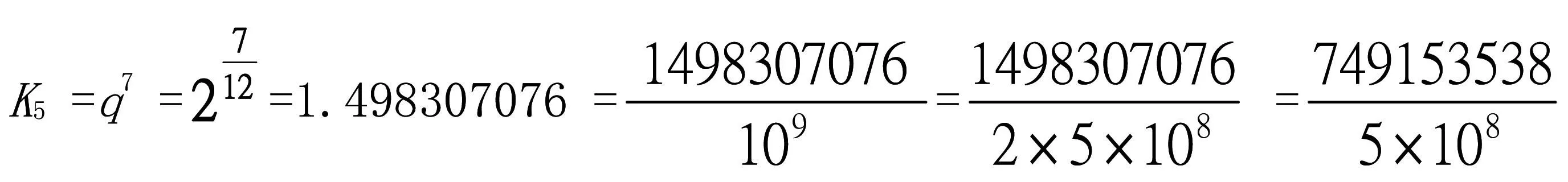

相生因子k5、k4以弦长比表示时,不难发现、它们与朱载堉在《律历融通·附音义》、《律吕精义内篇》卷一《不拘隔八相生第四》和《算学新说》三书中所述的完全一样。如此,不能不佩服朱载堉在创建新法密率中所做的音乐学和乐律学的贡献!如果知道起始音的频率或弦长,就可以用上述三种计算方法中的任何一种算出相应的等程律音阶。正如朱载堉所做的一样,十二等程律的音阶计算还有多种方法,诸如半音的上生或下生,它们都是根据等比数列的数学特性而做出的。
以上各种计算是乐律学或音乐数学的重要内容之一。历史上音乐家、科学家和文化思想大家中不乏主张,音乐是从属于数学的学科,其原因大概如此。在这些主张中,除了上古时一些贤哲的言论外,中世纪神学家阿奎那(T.Aguinas, 1225-1275)说:“音乐的基础是数学”。欧几里得(Euclid,前330-前275)《几何原本》的第一个英译者、炼金术士和数学家约翰·迪(John Dee,1527-1608)说:“音乐是一门数学科学”。法国数学家、音乐家梅森(Marin Mersenne,1558-1648)*习惯译名“梅森”,笔者时或按法语译为“默森”。是《和声学通论》的作者,他认为“音乐不外是发声的代数”。德国著名的科学文化情报人基歇尔(A.Kircher,1601-1680)著《音乐学通论》,他提出“音乐的操作模式是算术”,“音乐是从属于数学的学科”。中国的音乐理论家、十二等程律的发明人朱载堉(1536-1611)说:“乐也者,声音之学也;律也者,数度之学也”。近代科学的创始人开普勒(J.Kepler,1571-1630)、笛卡尔(Rene Descartes,1596-1650)、莱布尼兹(G.W.F.von Leibniz, 1646-1716),音乐家、作曲家巴赫(J.S.Bach, 1685-1750)等人都曾有过类似看法。但是,人们至今仍有疑问的是、为什么人类史上最早决定用“五度相生”(频率比为3/2)或“三分损益”(弦长比为2/3)而不是其他?为什么音乐家对于诸如以5/4(纯律大三度)代替81/64(五度律三度)极感兴趣?人们追求简单比数的音程,其原因在哪?实际上,毕达哥拉斯曾经发现、两个长度比愈简单的弦,他们所产生的声音的谐和程度就愈圆满。18世纪时,瑞士著名数学家欧拉(L.Eular,1707-1783)宣称,“人类的灵魂要在简单的数字比中取得性格上的爱好。”[8]赫尔姆霍茨从拍和拍音的实验中发现,“随着两个乐音的音调之差变化到使拍的干扰作用越来越明显,那么这两个音的频比数就越来越大。”[1]118-119这就解释了为什么较简单频比数的音程更令人愉快,因为此时拍的干扰愈小、甚而无干扰。笔者曾指出,频比数愈简单的音程,听感愈敏锐且愉悦。这个音乐生理现象或许也是一种回答。
作者附言:感谢中国音乐学院音乐科技系硕士生杨波先生帮助电脑输入和排版。
参考文献:
[1]H.von Helmhotz.OntheSensationofTone.Trans.Rev.andCorr[M].Alexander J. Ellis.New York:Dover Pub.Inc. 1954.
[2]戴振铎.广义三分损益律与朱载堉十二平均律及纯律的关系[J].中国音乐学,2000(4):105-114.
[3]戴念祖.消亡了的平均律[J].星海音乐学院学报,2015(2):35-39.
[4]Gene J. Cho.TheDiscoveryofMusicalEqualTemperamentinChinaandEuropeinthe16thCentury[M]. New York:The Edwin Mellen Press, 2003:233.
[5]朱载堉.律学新说:卷一[M].明万历本.
[6]H.J.Gray, A.Issacs.Edt.ANewDictionaryofPhysics[M].London:Longman,1975:190.
[7]S.Sadie. MacMillan.TheNewGroveDictionaryofMusicandMusician[M].London, New York:McMillan,1980,Vol.16:218.
[8]弗·卡约里.物理学史[M].戴念祖,译;范岱年,校.桂林:广西师范大学出版社,2002:208.
【责任编辑:吴志武】
中图分类号:J612.1
文献标识码:A
文章编号:1008-7389(2016)01-0082-09
DOI:10.3969/j.issn.1008-7389.2016.01.010
作者简介:戴念祖(1942-),男,福建长汀人,曾任中国科学院自然科学史研究所研究员,首都师范大学讲座教授,中国音乐学院音乐科技系特聘教授,主要从事科学史研究。
收稿日期:2015-08-30

