BCH-代数的BCHK-部分

李金龙，杨凯凡

(陕西理工学院 数学与计算机科学学院,陕西 汉中 723000)



BCH-代数的BCHK-部分

李金龙，杨凯凡

(陕西理工学院 数学与计算机科学学院,陕西 汉中 723000)

摘要:研究BCH-代数X的BCHK-部分即B(X),给出BCH-代数X中两个元素的乘积属于B(X)的几个条件.证明了: BCH-代数X的商代数〈X/ B(X)﹔*,C0〉是一个广义结合BCI-代数且C(0 )=B(X);在一个偏序BCH-代数X中,如果 X中的任一链都有下界,则|X/B(X)|等于X中极小元的个数.

关键词:BCH-代数;BCHK-部分;偏序BCH-代数;理想;商代数

相关文献提出了BCK-代数[1]、BCI-代数[2]、BCH-代数[3].众所周知,BCK-代数类是BCI-代数类的真子类,而BCI-代数类又是BCH-代数类的真子类,因此BCH-代数是最广泛的一类代数系统.BCI-代数的一些结论在BCH-代数中成立,一些则不成立；一些可直接推广,一些则不能直接推广.这是因为在BCI-代数中许多重要结论的证明都与公理[(x*y)*(x*z)]*(z*y)=0有关,而在BCH-代数中没有这一条公理,且BCI-代数中的一些基本性质在BCH-代数中也是不成立的.正是由于以上原因,对BCH-代数的研究就更加困难一些,只有通过别的途径来研究BCH-代数, 这样所得的结果更具有普遍性.作者提出了BCHK-代数的概念,将对BCH-代数的BCHK-部分即B(X)进行一些研究,同时讨论由B(X)所确定的BCH-代数商代数的一些性质.

为行文方便,先引入下面的一些定义和引理.

定义1[3]一个(2,0)型代数〈X﹔*,0〉叫做BCH-代数,如果∀x,y,z∈X,它满足下列公理

H-1x*x=0；

H-2x*y=y*x=0⟹x=y；

H-3(x*y)*z=(x*z)*y.

定义2[4]设〈X﹔*,0〉是一个BCH-代数,若∀x∈X,有0*x=0成立,则称〈X﹔*,0〉是一个BCHK-代数.

定义3[7]设〈X﹔*,0〉是一个BCH-代数,若

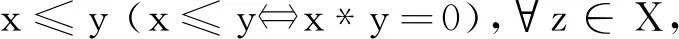
有

则称〈X﹔*,0〉是一个偏序BCH-代数.

若x≤y,∀z∈X,有z*y≤z*x, 这个性质称为BCH-代数的偏序性.

定义4[8]设〈X﹔*,0〉是一个BCH-代数,X的一个非空子集A被称为一个理想,如果它满足

(1) 0∈A;

(2) x∈A,y*x∈A⟹y∈A.

引理1[6，8]设〈X﹔*,0〉是一个BCH-代数,则∀x,y∈X,有下列结论成立

(1) 0*(x*y)=(0*x)*(0*y)；

(2) [x*(x*y)]*y=0;

(3) 0*[0*(0*x)]=0*x;

(4) x*0=x.

引理2[9]设A是BCH-代数〈X﹔*,0〉的一个理想,在X中定义一个二元关系:∀x,y∈X,x～y⟺0*(x*y)与0*(y*x)∈A,则～是X中的一个同余关系.记

定义

则〈X/A﹔*,C0〉是一个广义结合BCI-代数,且B(X)⊆C0.

引理3[9]设〈X﹔*,0〉是一个BCH-代数,令B(X)={x∈X:0*x=0},则B(X)是X的一个子代数,且B(X)是X的一个理想.

引理4[7]设〈X﹔*,0〉是一个偏序BCH-代数,则X中的二元关系≤是一个偏序关系.

1BCHK-部分的性质

在文[4]中,作者提出了BCHK-代数的概念.设〈X﹔*,0〉是一个BCH-代数, 令B(X)={x∈X:0*x=0},显然0∈B(X),称B(X)为BCH-代数〈X﹔*,0〉的BCHK-部分.下面对BCH-代数的BCHK-部分即B(X)进行一些研究,给出BCH-代数中两个元素之积属于B(X)的几个条件.

在文[5]中有结论:设〈X﹔*,0〉是一个BCI-代数,则∀x,y∈X,有[0*(x*y)]*(y*x) =0成立.文[5]是用BCI-代数中的公理[(x*y)*(x*z)]*(z*y)=0来证明的,而BCH-代数中无这一公理,但仍有下面的定理1.

定理1设〈X﹔*,0〉是一个BCH-代数,则∀x,y∈X,有

证明由引理1的(1),H-3,引理1的(2)和H-1,得

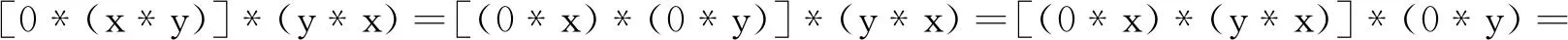
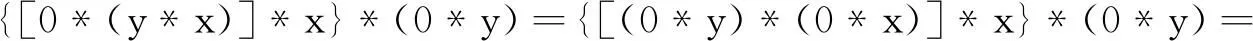
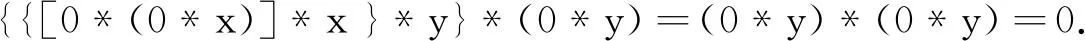
由H-3,知[0*(x*y)]*(y*x)=0⟺[0*(y*x)]*(x*y)=0,从而

所以，有

定理2设〈X﹔*,0〉是一个BCH-代数,∀x,y,a∈X,若x*a=0,y*a=0,则x*y∈B(X).

证明因为y*a=0∈B(X),由定理1得, a*y∈B(X),故0*(a*y)=0,再由H-1,条件x*a=0,引理1的(1)和(2),H-3，得

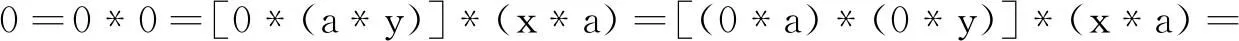
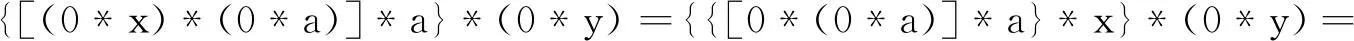
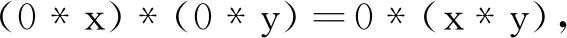
即0*(x*y)=0,所以x*y∈B(X).

该定理的几何意义是:从BCH-代数的乘法表上看,在元素a所在的那一列中,元素0所在的行对应的元素x和y的乘积x*y一定属于B(X).

定理3设〈X﹔*,0〉是一个BCH-代数,∀x,y,a∈X,若a*x=0,a*y=0,则x*y∈B(X).

证明因a*x=0,a*y=0,由H-1，得 0*(a*x)=0,0*(a*y)=0,再由引理1的(1),H-3,引理1的(2)和(3),得

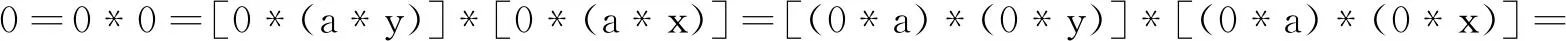
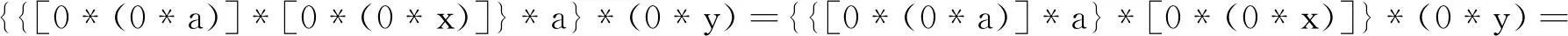
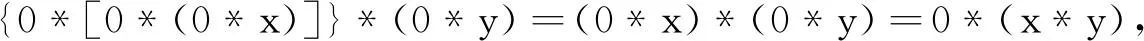
即0*(x*y)=0,所以x*y∈B(X).

该定理的几何意义是:从BCH-代数的乘法表上看,在元素a所在的那一行中,元素0所在的列对应的元素x和y的乘积x*y一定属于B(X).

注定理2的证明也可采用定理3的证明过程.这是因为x*a=0=y*a=0∈B(X),由定理1，得0*(a*x)=0,0*(a*y)=0,故由定理3的证明过程，知0=[0*(a*y)]*[0*(a*x)]=0*(x*y),所以x*y∈B(X).

定理4设〈X﹔*,0〉是一个偏序BCH-代数,∀x,y∈X,则x*y∈B(X)⟺∃a∈X,使a≤x,a≤y,即a*x=0,a*y=0.

证明充分性.由定理3,知显然成立.

必要性.因x*y∈B(X),故0*(x*y)=0,即0≤x*y,由偏序性和引理1的(4),得

又由引理1的(2),得

取

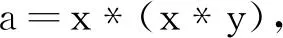
有

a≤x,a≤y.

该定理必要性的几何意义是:设〈X﹔*,0〉是一个偏序BCH-代数,若x≠y,有x*y∈B(X),则在乘法表中,一定有一行使元素0至少出现两次.

2由BCHK-部分确定的BCH-代数商代数的性质

定理5设〈X﹔*,0〉是一个BCH-代数,在X中定义一个二元关系

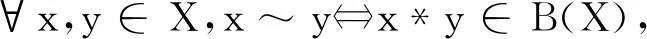
则～是X中的一个同余关系.

记

定义

则〈X/ B(X)﹔*,C0〉是一个广义结合BCI-代数,且C0=B(X).

证明由引理3知,B(X)是BCH-代数〈X﹔*,0〉的理想.先证明0*(x*y)与0*(y*x)∈B(X)等价于x*y∈B(X).

若0*(x*y)∈B(X),则由定理1和引理1的(4),得

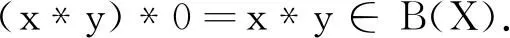
若

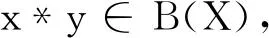
由定理1，得

故

0*(x*y)=0,

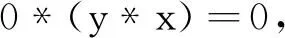
0*(x*y)与0*(y*x)∈B(X).

再证C0=B(X).设x∈C0,则x～0,故x*0=x∈B(X),即C0⊆B(X),由引理2知, B(X)⊆C0,所以C0=B(X).

综合上述,由引理2,知定理得证.

文[10]作者提出了广义结合BCI-代数,且有很好的性质,上面的定理将BCH-代数与广义结合BCI-代数联系起来了.

文[11]作者在BCI-代数中引入了渗透与极大渗透等概念,而一般的BCH-代数没有BCI-代数中的自然偏序关系,而由引理4知,偏序BCH-代数X中的二元关系≤是一个偏序关系,故作者将在偏序BCH-代数中引入渗透与极大渗透等概念,并进行一些研究.

定义5设〈X﹔*,0〉是一个偏序BCH-代数, a∈X,B⊆X且B≠Ø,记A(a)={x∈X:a≤x}, A(B)={x∈X:b≤x,b∈B},称A(a)是元素a的上截断, A(B)是集合B的上截断.如果B满足

(1) B=A(B);

(2)∀x,y∈B,∃b∈B,使b≤x,b≤y.

则称B是X的一个渗透.称X的渗透B是极大渗透,是指如果D是X的任一渗透,B⊆D,则B=D.

按定义显然有, a∈A(a);∀b∈B,b∈A(B),故B⊆A(B).

定理6设〈X﹔*,0〉是一个偏序BCH-代数, B⊆X且B≠Ø,则B是X的极大渗透的充要条件为B∈X/B(X).

证明充分性.设Cx∈X/B(X), 显然Cx⊆A(Cx);∀y∈A(Cx),由A(Cx)的定义知,∃a∈Cx,使a≤y,故a*y=0∈B(X),再由定理5知,a～y,又x～a,利用关系～的传递性得,x～y,故y∈Cx, 从而A(Cx)⊆Cx，所以Cx=A(Cx).∀a,b∈Cx,则a*b∈B(X),由定理4，得∃c∈X,使c≤a, c≤b. 因c*a=0∈B(X),故c～a,又x～a,从而c～x,c∈Cx.所以Cx是X的一个渗透.

设D是X的一个渗透,且Cx⊆D;则∀d∈D,因为x∈Cx⊆D,根据渗透的定义知,∃c∈D,使c≤x,c≤d,则c～x,c～d,故d～x,推出d∈Cx,D⊆Cx，从而Cx=D.所以Cx是X的极大渗透.

必要性.任取a∈B, 因B是X的渗透,∀x∈B,∃b∈B,使b≤x,b≤a,则b～x,b～a，故x～a,x∈Ca,从而B⊆Ca.由充分性知Ca是X的渗透,又B是X的极大渗透，所以B=Ca∈X/B(X).

该定理说明了在偏序BCH-代数中X的任一极大渗透都是X/B(X)中的一个等价类,而X/B(X)中的任一等价类都是X的一个极大渗透,所以极大渗透就是等价类.

定理7设〈X﹔*,0〉是一个偏序BCH-代数,若X中的任一链都有下界,记M={x∈X:x是X的极小元},则有|X/B(X)|=|M|.

证明任取Ca∈X/B(X),设A是Ca中的任一链,由已知条件知,A在X中有下界;设k是A的一个下界,则∀x∈A⊆Ca,有k≤x,故k*x=0∈B(X),从而k～x,又x～a,故k～a, k∈Ca.所以Ca中的任一链在Ca有下界,根据Zorn引理,Ca中至少存在一个极小元α.

假设β是Ca中又一个极小元,则α～β,故α*β∈B(X);由定理6知, Ca是X的一个极大渗透,故∃γ∈Ca,使γ≤α,γ≤β,由α与β都是极小元得,α=β=γ.这说明Ca有且仅有一个极小元α.

∀x∈X,若x≤α,则x～α,又α～a，故x～a，x∈Ca.由α是Ca中的极小元知x=α,因此α是X的极小元.所以Ca中有且仅有X中的一个极小元.

作映射φ: X/B(X)→M,∀Ca∈X/B(X),使φ(Ca)=α( α是X中的极小元),则∀α∈M,有Cα∈X/B(X),使φ(Cα)=α,故φ是满射.又∀Ca,Cb∈X/B(X), Ca≠Cb,则Ca∩Cb=Ø,从而Ca中的极小元α与Cb中的极小元β不相等,即φ(Ca)=α≠β=φ(Cb),故φ是单射.说明φ是X/B(X)到M的一一映射,所以|X/B(X)|=|M|.

在文[12]中,作者研究了BCH-代数X的原子与分支,把X中所有原子做成的集合记为L(X),证明了L(X)是BCH-代数X的一个广义结合BCI-子代数.原子的概念实质上就是极小元的概念,因此该定理说明了偏序BCH-代数商代数集合的基数与它的广义结合BCI-子代数集合的基数是相等的,即|X/B(X)|=|L(X)|.

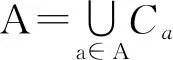
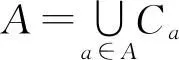
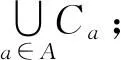
设a∈A,b∈X-A,假定b*a∈A,因A是X的理想,故b∈A,这与b∈X-A矛盾,所以b*a∉A.

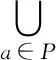
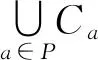
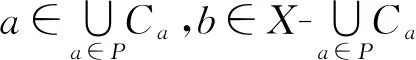
参考文献：

[1]IMAIY，ISEKIK.Onaxiomsystemsofpropositionalcalculi[J].ProcJapanAcad, 1996, 42： 19-22.

[2]ISEKIK.OnBCI-algebras[J].MathSeminarNotes, 1980, 8: 125-130.

[3]HUQP，LIX.OnBCH-algebras[J].MathSeminarNotes, 1983, 11: 313-320.

[4]李金龙,李军.关于BCH-代数导出半群的一些结果[J].安徽大学学报(自然科学版), 2015, 39(4): 1-4.

[5]孟杰,刘用麟.BCI-代数引论[M].西安:陕西科学技术出版社, 2001.

[6]李金龙.拟结合BCH-代数[J].黄冈师范学院学报(自然科学版), 2003, 23(3): 19-21.

[7]李金龙.偏序BCH-代数的一种自映射[J].河北大学学报(自然科学版), 2006, 26(3): 242-245.

[8]胡庆平.BCI-代数[M].西安:陕西科学技术出版社, 1987.

[9]李金龙.BCH-代数与广义结合BCI-代数的关系[J].汉中师范学院学报(自然科学版), 2002, 20(2): 25-29.

[10]雷天德.广义结合BCI-代数[J].纯粹数学与应用, 1985, 1: 98-102.

[11]王文良. BCI-代数序结构的特征[J].西北师范大学学报(自然科学版), 1991, 27(3): 10-15.

[12]李金龙. BCH-代数的原子与分支[J].纯粹数学与应用, 2003, 19(2): 145-148.

(责任编辑朱夜明)

BCHK-parts of BCH-algebras

LI Jinlong， YANG Kaifan

(College of Mathematics and Computer Science, Shaanxi University of Technology, Hanzhong 723000, China)

Abstract:The BCHK-part i.e. B(X) of the BCH-algebra X was researched, several conditions that the product of two elements in X belonged to the B(X) were given. It was proved that the quotient algebra 〈X/ B(X)﹔*, C0〉of a BCH-algebra X was a generalized associative BCI-algebra and C(0 )=B(X), and in a partial ordering BCH-algebra X, if any chain had lower bound , then |X/B(X)| was equal to the number of minimal element in X.

Key words:BCH-algebra; BCHK-part; partial ordering BCH-algebra; ideal; quotient algebra

中图分类号：O152

文献标志码:A

文章编号:1000-2162(2016)03-0001-05

作者简介：李金龙(1961-),男,陕西户县人,陕西理工学院教授.

基金项目:国家自然科学基金资助项目(11301318); 陕西理工学院重点科研基金资助项目(SLGKY14-03)

收稿日期：2015-04-13

doi:10.3969/j.issn.1000-2162.2016.03.001