M-矩阵Fan积的最小特征值下界的新估计

陈付彬, 赵建兴

(1.昆明理工大学 津桥学院，云南 昆明 650106; 2.贵州民族大学 理学院, 贵州 贵阳 550025)



M-矩阵Fan积的最小特征值下界的新估计

陈付彬1, 赵建兴2

(1.昆明理工大学 津桥学院，云南 昆明 650106; 2.贵州民族大学 理学院, 贵州 贵阳 550025)

摘要:利用Cauchy-Schwitz不等式给出非奇异M-矩阵A和B的Fan积A★B的最小特征值下界的新估计式，并与其他文献中的估计式进行比较.数值算例表明，新估计式在一定条件下改进了Johnson和Horn给出的经典估计式，同时也优于其他已有的几个估计式，比现有的估计式更接近真值.

关键词:M-矩阵；Fan积；最小特征值；下界

M-矩阵不仅是计算数学和矩阵理论的重要研究课题之一, 而且在生物学、物理学、经济数学等诸多领域都有着重要的实用价值. 矩阵Fan积是一种特殊的矩阵乘积, 被广泛应用于偏微分方程中的弱极小原理和概率论中特征函数等方面的研究中. 在这些研究中, 非奇异M-矩阵Fan积的最小特征值下界的估计成为研究热点之一, 并得到了一系列相关的估计式[1-11]. 文中将对这一问题做进一步探讨，给出非奇异M-矩阵Fan积的最小特征值τ(A★B)下界的一个新估计式, 该结果在一定条件下比现有的一些结果更加精确.

1预备知识

用Cn×n(Rn×n)表示n阶复(实)矩阵集,记N={1,2,…,n}.若aij≥0(aij>0)，则称A是非负矩阵(正矩阵)，记为A≥0(A>0), 矩阵A=(aij)∈Cn×n的n个特征值λ1,λ2,…,λn组成的集合称为矩阵的谱，记为σ(A).特征值的模的最大值称为矩阵A的谱半径, 记为ρ(A). 若A为非负矩阵，则由Perron-Frobenius定理知,ρ(A)∈σ(A), 且有非负特征向量x与之对应, 满足Ax=ρ(A)x[12].

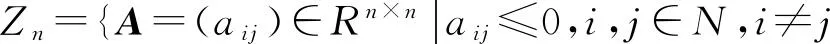
令A∈Zn, 记τ(A)=min{Re(λ):λ∈σ(A)}，由文献[1]中的结论知:τ(A)∈σ(A), 称τ(A)为A的最小特征值.

设A是非奇异M-矩阵, 则存在正向量u,v,使得Au=τ(A)u,vTA=τ(A)vT, 其中u和v分别称为矩阵A的右Perron特征向量和左Perron特征向量.

假设A,B∈Mn, 则A,B的Fan积定义为A★B=C=(cij),有

由文献[1]中的结论知：若A,B∈Mn, 则A★B∈Mn.

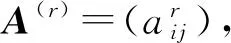
对于M-矩阵A和B的Fan积最小特征值下界的估计, 前人做了很多研究. 1991年,Johnson和Horn在文献[1]中给出一个经典的结果

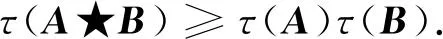
(1)

方茂中改进上述不等式, 在文献[2]中给出如下结果

(2)

黄荣同样对不等式(1)进行改进，在文献[3]中给出如下结果

(3)

刘庆兵改进不等式(2), 在文献[4]中给出下面结果

(4)

李耀堂改进文献[1-3]的结果，在文献[5]中给出如下结果

(5)

其中

论文将给出τ(A★B)的新下界作为对前人研究结果的有益补充, 并且保证这个新的下界比现有的一些经典结果更接近于τ(A★B)的真实值, 且新结果将包含文献[4]中的结论.

2主要结果

引理1设a=(a1,a2,…,an)T≥0，b=(b1,b2,…,bn)T≥0, 则

其中：m=1,2.

证明由Cauchy-Schwitz不等式容易证明结论成立.

引理2[1]设A,B是非奇异M-矩阵, D,E是正的对角矩阵, 则

引理3[14]设A=(aij)∈Cn×n, 则A的所有特征值都位于复平面的下列区域

定理1设A=(aij), B=(bij)∈Rn×n是非奇异M-矩阵, 则

(6)

其中：m=1,2.

证明显然n=1, 式(6)成立, 下面假设n≥2.

若A★B不可约, 则A和B是不可约的M-矩阵，且分别存在正向量

使得

即

设

U=diag(u1,u2,…,un),V=diag(v1,v2,…,vn).

令

即

且

由引理2可知

所以

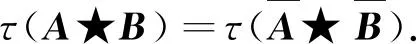
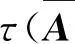
(7)

由不等式(7)，得

所以，有

若A★B为可约矩阵,Zn中的矩阵是非奇异M-矩阵的充分必要条件是其所有顺序主子式为正[15]. 定义T=(tij)为n阶置换阵, 其中t12=t23=…=tn-1,n=tn,1=1, 其余元素为零.对于足够小的ε>0, A-εT,B-εT的所有顺序主子式为正,所以，当ε>0足够小时，A-εT, B-εT均是不可约的M-矩阵. 用A-εT,B-εT代替A,B，再令ε→0,则由连续性知结论(6)仍然成立.

在定理1中令m=1,得

即是文献[4]中定理7的结果.

3数值算例

为方便计算，利用文献[5]中的例子，令

所以

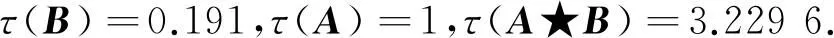
依据式(1)，得

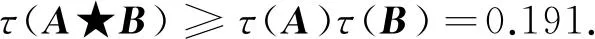
依据式(2)，得

依据式(3)，得

依据式(4)，得

依据式(5)，得

在论文定理1中令m=2，得

参考文献：

[1]HORN R A, JOHNSON C R. Topics in matrix analysis[M]. New York: Cambridge University Press, 1991.

[2]FANG M Z. Bounds on eigenvalues of the Hadamard product and the Fan product of matrices[J]. Linear Algebra Appl, 2007, 425(1):7-15.

[3]HUANG R. Some inequalities for the Hadamard product and the Fan product of matrices[J]. Linear Algebra Appl, 2008, 428(7): 1551-1559.

[4]LIU Q B, CHEN G L. On two inqualities for the Hadamard product and the Fan product of matrices[J]. Linear Algebra Appl, 2009, 431(5/6/7): 974-984.

[5]LI Y T, LI Y Y, WANG R W, et al. Some new bounds on eigenvalues of the Hadamard product and the Fan product of matrices[J]. Linear Algebra Appl, 2010, 432(2/3): 536-545.

[6]李艳艳, 李耀堂. 矩阵Hadamard积和Fan积的特征值界的估计[J]. 云南大学学报(自然科学版)，2010, 32(2): 125-129.

[7]周平, 李耀堂. M-矩阵及非负矩阵Hadamard积和Fan积的特征值界的估计[J]. 云南大学学报(自然科学版)，2012, 34(1): 9-14.

[8]李华. 矩阵Hadamard积和Fan积特征值界的新估计式[J]. 河南科学, 2012, 30(6): 680-683.

[9]LIU Q B, CHEN G L, ZHAO L L. Some new bounds on the spectral radius of matrices[J]. Linear Algebra Appl, 2010, 432(4): 936-948.

[10]杜琨. 矩阵Hadamard积和Fan积特征值的界[J]. 华东师范大学学报(自然科学版)， 2008(5): 45-50.

[11]朱雪芳. 矩阵Fan积特征值的界[J]. 数学的实践与认识， 2012， 42(2): 209-213.

[12]黄廷祝，杨传胜. 特殊矩阵分析及应用[M]. 北京：科学出版社， 2003.

[13]陈景良，陈向辉. 特殊矩阵[M]. 北京：清华大学出版社， 2000.

[14]HORN R A, JOHNSON C R. Matrix analysis [M]. New York: Cambridge University Press, 1985.

[15]BERMAN A, PLEMMONS R J. Nonnegative matrices in the mathematical sciences[M]. New York: Academic Press, 1979.

(责任编辑朱夜明)

New estimation on lower bound for the minimum eigenvalue of the Fan product of M-matrices

CHEN Fubin1， ZHAO Jianxing2

(1. Oxbridge College, Kunming University of Science and Technology, Kunming 650106, China；2. College of Science, Guizhou Minzu University, Guiyang 550025, China)

Abstract:A new lower bound on the minimum eigenvalue for the Fan product A★B of two nonsingular M-matrices A and B was given by using Cauchy-Schwitz inequality and compared the new bound with the classical results in the literature. Numerical example showed that the new estimating formula improve the result of Johnson and Horn effectively in some cases, and also was better than the other existing results, which approached the real value than existing ones.

Key words:M-matrix; fan product; minimum eigenvalue; lower bound

中图分类号：O151.21

文献标志码:A

文章编号:1000-2162(2016)03-0012-05

作者简介：陈付彬(1979-)，男，山东临沂人，昆明理工大学副教授.

基金项目:国家自然科学基金资助项目(71161020, 11501141)；云南省教育厅科学研究基金资助项目(2013C165, 2015C107Y)

收稿日期：2015-03-11

doi:10.3969/j.issn.1000-2162.2016.03.003