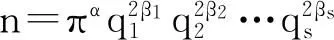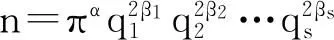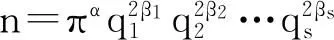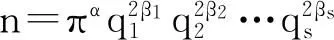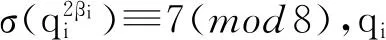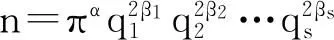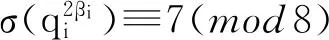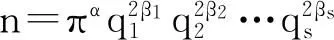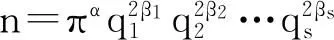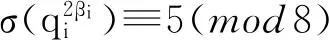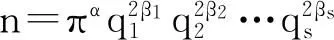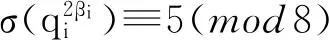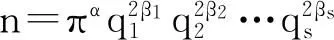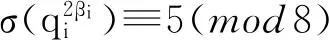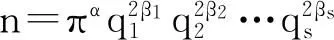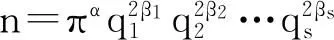奇合数n不是完全数的一些命题

张四保

(喀什大学 数学与统计学院,新疆 喀什 844008)



奇合数n不是完全数的一些命题

张四保

(喀什大学 数学与统计学院,新疆 喀什 844008)

摘要:奇完全数问题是数论中的一著名难题. 探讨形如4m+1的奇正整数是否为完全数问题，给出其在σ(π(α))≡2(mod8)条件下不是完全数的一些命题，由此可以类似地讨论其在σ(π(α))≡6(mod8)条件下的情形，从而可以给出4m+1型合数不是完全数的一系列条件.

关键词:完全数；奇完全数；条件

初等数论是密码学研究的重要基础理论[1]，其有着很多的研究热点课题.设σ(n)是正整数n所有正约数(包括1与n)的和函数.如果正整数n满足σ(n)=2n，则n被称为完全数.完全数问题是数论中的著名难题之一，许多学者对其进行了探究. 截至目前，人们只发现了49个完全数，且它们都是偶数.是否存在奇完全数，这已成为数论中的一难题[2]. 因而研究是否存在奇完全数，或者给出某奇正整数不是完全数的条件，是数论中一项十分有意义的工作.

Euler研究给出了奇完全数n的形式为

(1)

其中：π与qi(i=1,2,…,s)为互素的奇素数；q1，q2，…，qs是满足q1

1主要结论

当n是形如(1)式且为4m+1型的奇合数时，由于σ(n)是积性函数，有

由于π≡α≡1(mod4)，则π≡α≡1,5(mod8). 因而，当π≡1(mod8)时，有

当π≡5(mod8)时，有

其中：k是使得α=4k+1成立的非负整数.

此时，当k≡0(mod2)，有σ(πα)≡6(mod8)；当k≡1(mod2)，有σ(πα)≡2(mod8).

综合以上讨论，恒有

由于

8m+2≡2(mod8)，

则当σ(πα)≡2(mod8)时，有

当σ(πα)≡6(mod8)时，有

由于qi(i=1,2,…,s)为奇素数，则qi可写成qi≡±1(mod8)，qi≡±3(mod8)这4种形式.

当qi≡1(mod8)时，有

(2)

当qi≡-1(mod8)时，有

(3)

当qi≡3(mod8)时，有

(4)

当qi≡-3≡5(mod8)时，有

(5)

证明当qi都满足qi≡1(mod8)，qi的指数2βi满足βi≡1(mod4)时，有

此时，当s≡1(mod2)，即s为奇数，有

当qi都满足qi≡1(mod8)，qi的指数2βi满足βi≡3(mod4)时，有

此时，当s≡1(mod2)，即s为奇数，有

而当σ(πα)≡2(mod8)，有

因而，此时n不是完全数.证毕.

证明qi都满足qi≡1(mod8)，qi的指数2βi满足βi≡1(mod4)时，有

qi的指数2βi满足βi≡2(mod4)时，有

qi的指数2βi满足βi≡3(mod4)时，有

此时，当指数满足βi≡1(mod4)的素因子个数为偶数个，满足βi≡2(mod4)与βi≡3(mod4)的素因子个数都为奇数个，有

当指数满足βi≡3(mod4)的素因子个数都为偶数个，满足βi≡1(mod4)与βi≡2(mod4)的素因子个数都为奇数个，有

此时，当指数满足βi≡1(mod4)与βi≡2(mod4)的素因子个数都为奇数个，有

当指数满足βi≡1(mod4)个数为奇数个，而满足βi≡2(mod4)的素因子个数为偶数个，有

此时，当指数满足βi≡1(mod4)的素因子个数为奇数个，满足βi≡2(mod4)与βi≡3(mod4)的素因子个数都为偶数个，有

当指数满足βi≡3(mod4)的素因子个数为奇数个，满足βi≡1(mod4)与βi≡2(mod4)的素因子个数都为偶数个，有

此时，当满足qi≡1(mod8)的素因子的个数为奇数个，满足qi≡3(mod8)的素因子的个数为奇数个时，有

当满足qi≡1(mod8)的素因子的个数为奇数个，满足qi≡3(mod8)的素因子的个数为偶数个时，有

因而，此时n不是完全数.证毕.

此时，当满足qi≡1(mod8)的素因子的个数为奇数个，满足qi≡5(mod8)的素因子的个数为奇数个时，有

当满足qi≡1(mod8)的素因子的个数为偶数个，满足qi≡5(mod8)的素因子的个数为奇数个时，有

因而，此时n不是完全数.证毕.

此时，当满足qi≡3(mod8)与qi≡5(mod8)的素因子的个数都为奇数个，有

当满足qi≡3(mod8)的素因子个数为偶数个，而满足qi≡5(mod8)的素因子的个数都为奇数个，有

因而，此时n不是完全数.证毕.

此时，当满足qi≡1(mod8)与qi≡3(mod8)的素因子的个数都为偶数，满足qi≡5(mod8)的素因子的个数为奇数个时，有

当满足qi≡1(mod8)与qi≡3(mod8)的素因子的个数都为奇数，满足qi≡5(mod8)的素因子的个数为奇数个时，有

因而，此时n不是完全数.证毕.

2结束语

参考文献：

[1]李滨.多元一次不定方程解的结构及其应用[J].安徽大学学报(自然科学版)， 2015， 39(5)： 6-12.

[2]盖伊．数论中未解决的问题[M]．张明尧,译. 北京：科学出版社， 2003．

[3]DICKSON L E． History of theory of number[M]． Washington: Washington Carnegie Institution, 1919．

[4]BRENT R P, COHEN G L, RIELE H J. Improved techniques for lower bounds for odd perfect numbers[J]. Math Comp, 1991, 57: 857-868.

[5]MICHA E, RAO I . Odd perfect numbers are greater than 101500[J]. Math Comp, 2012, 81(279): 1869-1877.

[6]NIEISEN P P. Odd perfect numbers have at least nine distinct prime factors[J]. Math Comp, 2007, 76: 2109-2120.

[7]GOTO T, OHNO Y. Odd perfect numbers have a prime factor exceeding 108[J]. Math Comp, 2008, 77: 1859-1868.

[8]PASCAL O, MICHA E, RAO I. On the number of prime factors of an odd perfect number[J]. Math Comp, 2013, 83 (289): 2435-2439.

[9]ZHANG S B. Some results of a certain odd perfect number[J].Chinese Quarterly Journal of Mathematics, 2014, 29(2): 167-170.

[10]MCDANIEL W L, HAGIS P. Some results concerning nonexistence of odd perfect numbers of the form pαm2β[J]. The J Fibonnacci Quart, 1975, 13 (1) : 25 -28.

[11]IANNUCCI D E, SORLI R M. On the total number of prime factors of an odd perfect number[J]. Math Comp, 2003, 72: 2078 -2084.

[12]STARNI P. On some properties of the Euler’s factor of certain odd perfect numbers[J]. J Number Theory, 2006, 116(1): 483- 486.

[13]朱玉扬.奇完全数的几个命题[J].数学进展， 2011， 40(5)： 595-598.

[14]管训贵.关于完全数的一点注记[J].青海师范大学学报(自然科学版)， 2014， 30 (4)：4-7.

(责任编辑朱夜明)

Several results on the positive odd numbersnis not perfect number

ZHANG Sibao

(School of Mathematics and Statistics, Kashgar University, Kashgar 844008,China)

Abstract:The problem of perfect number was a well-known difficult problem in number theory. In this paper, the problem that the positive odd numbers of the form 4m+1 was not perfect number was studied. And in the condition of σ(π(α))≡2(mod8), some results on the composite number be the form of 4m+1 was not perfect were given. Similarly, the conditions of was not odd perfect number in the condition of σ(π(α))≡6(mod8) can be discussed. Therefore, a series of conditions of the form of 4m+1 was not perfect number could be given.

Key words:perfect number; odd perfect number; condition

中图分类号：O156

文献标志码:A

文章编号:1000-2162(2016)03-0006-06

作者简介：张四保(1978-)，男，江西峡江人，喀什大学副教授.

基金项目:国家自然科学基金资助项目( 11201411)；喀什大学科研基金资助项目(142513)

收稿日期：2015-05-25

doi:10.3969/j.issn.1000-2162.2016.03.002