关于Nesbitt不等式的上、下界

浙江省湖州市双林中学　　李建潮　　(邮编：313012)



初数研究

关于Nesbitt不等式的上、下界

浙江省湖州市双林中学李建潮(邮编：313012)

著名Nesbitt不等式：若a、b、c∈R+,则

①

(1963年莫斯科数学竞赛试题)

本文探究Nesbitt不等式①(下界)的加强，并延探其上界不等式.

1Nesbitt不等式(下界)的加强

赛题 (1983年瑞士数学竞赛试题)已知a、b、c∈R+,求证：

②

定理1 若 a、 b、c∈R+,则

③

也曾在《中等数学》2007年第9期上看到Nesbitt不等式另一加强形式：

已知a、b、c∈R+,则

定理2若a、b、c∈R+,则

④

为此，不妨先给出以下恒等式：

引理1设a、b、c∈R+,则有

⑤

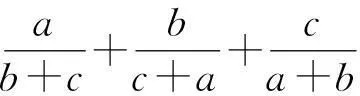
⑥

证明

即

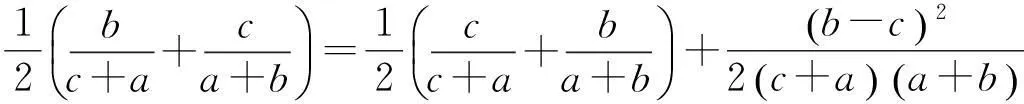
同理可得

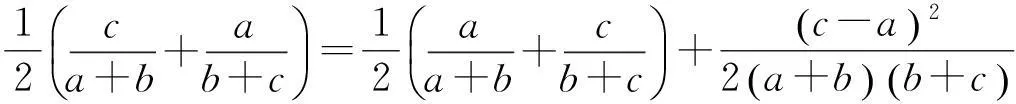
以上三式相加，即得⑤式；

下面转入定理2的证明：由a、b、c的对称性，而不妨设a≥b≥c>0.则a2≥b2≥c2,

定理2得证.

2Nesbitt不等式的上界

2.1顺手牵“羊”话上界

由引理1的⑤式，立马得到：

据此，顺手牵“羊”得到关于Nesbitt不等式的一个上界不等式：

定理3若a、b、c∈R+,则

⑦

⑧

2.1创建恒等式获取新上界

仿照引理1，再次创建恒等式：

引理2 设a、b、c∈R+,则有

⑨

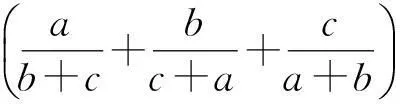
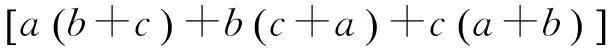
=a2+b2+c2+(bc+ca+ab)

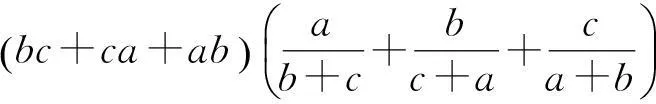
下面根据引理2探索关于Nesbitt不等式的新上界不等式：

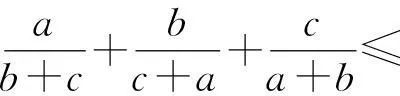
据此，得到关于Nesbitt不等式更强的新“上界”：

定理4若a、b、c∈R+,则

⑩

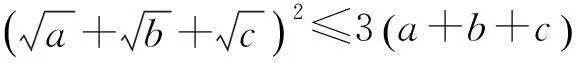
3让Nesbitt不等式加强的“下界”无上界

利用三维Cauchy(柯西)不等式，有

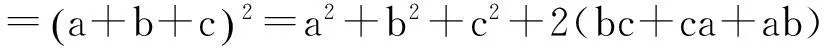
定理5 若a、b、c∈R+,则

如若直接应用作为恒等式的引理2，则将会是怎样一番景象呢？三维Cauchy不等式应用于⑨的右边，有

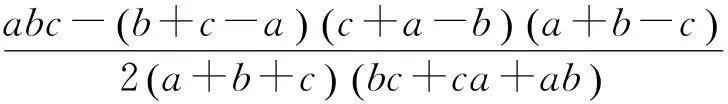
定理6若a、b、c∈R+,则

由此可见，由前面“怪异”证法得到的定理5是一个关于Nesbitt不等式“下界”的优美、和谐、精准、实用的不等式，而定理6则较定理5更科学化的了.

参考文献

1李建潮. 两个相关数学问题的加强[J].中学数学研究，2010(11)

(收稿日期：2016-01-25)