诊断问题症结做到高效复习

☉江苏省锡东高级中学滕陈英

诊断问题症结做到高效复习

☉江苏省锡东高级中学滕陈英

从近两年的江苏高考情况看，试卷中的解析几何题目一般是两小一大，分值在22分左右.二次曲线是高中数学的重要内容之一，涉及知识点多、知识面广，常与其他知识（方程、三角、函数等）彼此渗透，相互融合，是高考经典题型之一.二次曲线问题往往入手容易，但要善始善终，想获得正确完美的解答却不容易.笔者根据自己的教学实践，结合同学们在学习解析几何中常见的几类症状，有针对性地加以诊断，从而提出解决之法.

一、生搬硬套——忽视前提条件

例1若椭圆的一条准线方程为x=10，其相应的焦点为（4，0），离心率为，求此椭圆的方程.

点评：上述两种解法错误的原因是：误认为椭圆的方程是中心在原点的标准方程，从而生搬硬套乱用椭圆的标准方程，导致错误.实际上，只有曲线的中心在坐标原点，对称轴为坐标轴的情况下，才能直接套用标准方程的形式.

二、盲目互换——忽视条件的判断

例2求中心在原点，对称轴是坐标轴，一条渐近线方程为4x+3y=0，且过双曲线方程.

点评：上述解法错误的原因是：忽视焦点位置的探讨，贪图省事，盲目互换，以致出现错误.实际上，解决此类问题应该先判断双曲线的焦点位置，再设方程，事实上此题正是如此，焦点不在y轴上.

解：依题意知，双曲线的另一条渐近线方程为4x-3y=0，

三、未挖隐含——忽视二次曲线的性质“有界性”

错解：由2=4b2，椭圆方程可化1.

设P到椭圆上的点（x，y）的距离为d，

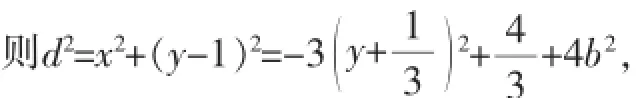
点评：上述解法错误的原因是：忽视了椭圆“有界性”，即椭圆是一个封闭曲线，在本题中动点（x，y）的纵坐标范围应为y∈［-b，b］，学生误认为时取得最

值，从而导致错误.解决此类问题应注意变量的值是否在对应范围内.

四、凭空想象——忽视图像的作用

例4一个动圆和已知圆x2+y2-2x=0外切，并与直线l∶x+y=0相切于点A（3，-），求该动圆的方程.

错解：设圆的方程为（x-a）2+（y-b）2=r2，已知圆的方程可化为（x-1）2+y2=1.

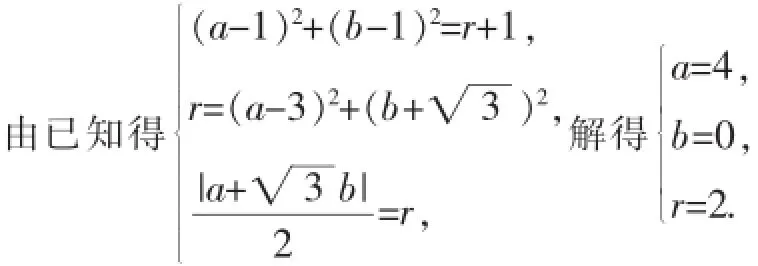
所以动圆的方程为（x-4）2+y2=4.

点评：上述解法正好验证了解析几何的特点：入手容易，坚持困难.此题思路正确，列式无误，但是计算困难，以致造成错误，遗漏了一组解.之所以出现如此情况，原因在于凭空想象，忽视了图像在解析几何中的重要作用.本题只要作出正确的图像，充分利用图形的几何性质，就能发现应该有两个结论，并且可以使运算简单化.

解：设动圆的圆心为P，已知圆的圆心为M，由已知两圆外切，则PM=1+PA.

由几何性质得动圆的圆心P在过点A且与直线l垂直的直线l′上，

五、以偏概全——忽视思想方法的应用

（1）已知椭圆短轴的两个三等分点与一个焦点构成

例5已知椭正三角形，求椭圆的方程；

（2）设过点F的直线l交椭圆于A，B两点，若直线l绕点F任意转动，恒有OA2+OB2＜AB2，求实数a的取值范围.

（2）设A（x1，y1），B（x2，y2），直线AB的方程为y=k（x-1），代入椭圆方程得

点评：直线与圆锥曲线的综合问题几乎年年都是重点考查的内容，但是上述解答错误的原因是：忽略了对直线斜率不存在这个特殊情况的讨论，导致解答不全面.直线的斜率存在时，解答同上.

教学感悟：“问渠哪得清如水，为有源头活水来”.纵观近几年的数学高考题，试题越来越“返璞归真”，既不需要深奥的知识，也没有高难的技巧，许多题目扎根于课本，由若干个基础知识经串联、加工、改造而成.因此在高三复习时要抓住主干知识进行强化复习，重视典例分析，通过引申、拓展、探究，做到解一题通一片，跳出题海，提高复习的实效性.G

验证得