一次数学选修课的实录和思考

☉江苏省海门市四甲中学沈敏鉴

一次数学选修课的实录和思考

☉江苏省海门市四甲中学沈敏鉴

数学选修课是对必修课程的一种良好补充，从学科体系来讲，数学选修比较适合开设知识拓展类等，主要以提高现有知识为主的教学比较合适.笔者选择的某次课堂是柯西不等式，基本不等式是高考的必考内容，是不等式中最基本的形态，柯西不等式是对基本不等式的补充，在解决一系列相关问题时不再需要多次基本不等式去实现，因此选修探索内容选择柯西不等式是比较切合数学教学实际的.

一、教学实录

1.缘自最近发展区，回顾a2+b2≥2ab的几何模型

师：这是2002年在北京举行的国际数学家大会的会标，源自我国古代著名的赵爽弦图（投影显示图1），图中用四个全等的直角三角形拼成了一个正方形.如果把直角三角形的两条直角边边长分别记为a、b，那么正方形的面积等于多少？

师：所以赵爽弦图中蕴含了怎样的不等关系？

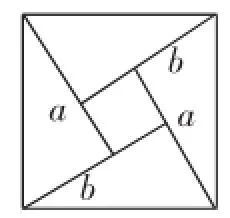
图1

生（集体）：a2+b2≥2ab.

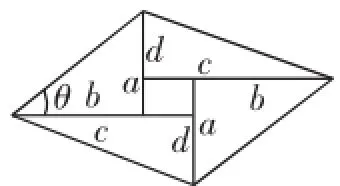
图5

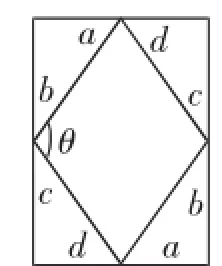
图6

师：大家能利用赵爽弦图说明上述不等式什么时候取等号吗？

生（集体）：当a=b时，四个三角形的面积和就等于正方形的面积.

师：这儿的a、b是三角形的边长，所以它们都是正数.但我们知道当a、b∈R时上述不等式均成立.我们是如何证明的？

生1：a2+b2-2ab=（a-b）2≥0.

师：很好，作差法是证明不等式最基础也是最重要的方法.

2.以小组合作形式，类比探究柯西不等式

师：以上是关于两个实数的不等式a2+b2≥2ab，赵爽弦图中用了四个全等的直角三角形，a、b分别是两条直角边边长.今天我们要更进一步，探究关于四个实数的不等式“（a2+b2）（c2+d2）≥？”，借用先贤的智慧，研究四个实数a、b、c、d需要怎样的三角形？a、b、c、d分别是什么？请大家大胆猜测.

生2：四个直角三角形，两两全等.a、b分别是其中两个全等的直角三角形的直角边边长，c、d分别是另两个全等的直角三角形的直角边边长.

师：非常好，让我们一起沿着这位同学的思路走下去.（教师发给各小组三角形模型，如图2）

图2

师：请同学们以小组为单位用这四块三角形拼成你们认为可以用来解决问题的图形.

学生代表上黑板展示：

图4

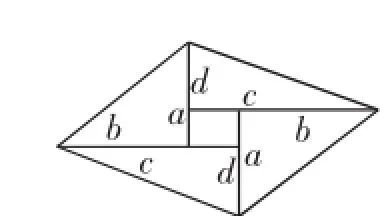
图3

师：老师看到有6个小组拼成平行四边形（如图3），2个小组拼成长方形（如图4），这两种图形都很棒.赵爽弦图中我们是从哪个角度思考得到不等式a2+b2≥2ab？

生3：图形的面积.

师：很好，请各小组按自己的图形继续你们的探究，思考其中蕴含的不等式.

教师巡视，给予指导.

学生代表1（平行四边形）：平行四边形的面积有两种算法：①如图3，把平行四边形看作由四个直角三角形和中间的长方形拼成，那么S平行四边形=ab+cd+（c-b）（a-d）=ac+bd.②如图5，设平行四边形一内角为θ，则S平行四边形=b2）（c2+d2）≥（ac+bd）2，当sinθ=1时取等号.

师：非常好，这样我们就得到（a2+b2）（c2+d2）≥（ac+ bd）2.这儿a，b，c，d取值范围是什么？

生4：a，b，c，d是三角形的边长，均为正数.

生5：a2+b2≥2ab在图形推导中仅对正数成立，但实际对一切实数都成立.这个不等式也可能这样.

师：那么这个不等式是不是对于任意实数都成立呢？让我们来进一步求证.

投影显示：试证明（a2+b2）（c2+d2）≥（ac+bd）2（a，b，c，d∈R）.

学生各自尝试，绝大多数能独立完成证明.

师：从证明中我们可以发现取等号的条件为ad=bc，这个推导过程哪个更准确？

生6：ad=bc.

师：这样我们就得到一个著名的不等式——柯西不等式的最简呈现方式，即二维形式.

3.从两个方向出发完成不等式的初步应用

师：下面让我们走进柯西不等式，请同学们完成下列填空：

（1）（x2+y4）（a4+b2）≥（_______+_______）2；

（2）（x2+y2）（_______+_______）≥（x+yz）2；

（3）（_______+_______）（m2+n2）≥（2mx+3ny）2.

生7：（1）（x2+y4）（a4+b2）≥（xa2+y2b）2；

（2）（x2+y2）（1+z2）≥（x+yz）2；

（3）（4x2+9n2）（m2+n2）≥（2mx+3ny）2.

师：这位同学的回答对吗？有没有不同的意见？

生：全对.

生8：（1）（x2+y4）（a4+b2）≥（xb+y2a2）2.

师：这位同学的回答正确吗？

生：也对.

师：所以我们在应用柯西不等式时要根据需要灵活处理.下面请大家思考下题，证明不等式.

应用1：已知a，b∈R，证明：（a4+b4）（a2+b2）≥（a3+b3）2.

师：哪位同学有思路？

生9：用柯西不等式直接可以证明.

（教师通过投影，引导其加以说明）

师：这道题用作差比较法也能解决，但过程没有如此简洁.

4.提炼探究方法提出新的问题

师：柯西不等式是著名数学家柯西发现，并以他命名的.今天同学们通过自己的努力探究也推导出了这个著名的不等式.我们在推导过程中运用了哪些数学思想方法呢？

生10：类比，由a2+b2≥2ab类比.

生11：数形结合，从图形中得到了不等式.

生12：在一开始决定要哪种三角形时进行了合情推理.

师：同学们总结得很好，你们说的这些是我们探究数学问题时的常用方法.数学王国还有很多未解决的问题，只要我们勇于探索，勤于思考，完全可以有所作为.今天我们推导出的仅是柯西不等式的二维形式，对于它的其他形式，大家有没有想法？

生13：三维形式，应该和空间向量有关系.

师：很好的想法，三维形式具体是怎样的？请大家课后思考.

二、教学反思

我们的数学选修课堂有时基于功利性的需要和认识的偏差，存在着去数学化现象.教师为了多讲一些题型，让学生多练习便“掐头去尾烧中段”，让我们的学生没有时间自己去发现问题、探究问题.在这样的数学课堂不可能培养学生高层次的思维能力，特别是探究能力.本节选修课设计以学生终身发展为目标，意在培养学生学习数学、探究问题的热情和能力.

1.多给“动起来”的机会，使学生乐于探究

课堂中学生动脑思考探究方法、动手拼图形、动笔进行运算、动口汇报成果，给学生充分“动起来”的机会，让学生充分展示自我，激发学生的学习热情，使他们乐于探究.对于学生拼成的两种图形都给予肯定，让他们有机会沿着自己的道路前进.培养学生个性化学习正是培养学生自主探究学习能力的目标.学生在对问题的探索时表现出较高的积极性.当他们自己推导并证明了二维形式的柯西不等式时，显得十分兴奋，情绪空前高涨.正式上课巡视时发现有一小组的学生用四个直角三角形拼了两个矩形，这是笔者多次课堂上都没有遇到的情况.当时认为这个图形与赵爽弦图相距较远，也害怕计划外的讨论会影响教学任务的完成，所以建议学生换个拼图方法.课后发现如果在图形外沿描绘一个矩形，这个矩形和图4中的一样.把两张图结合起来，利用空白部分的面积，可以马上得到等式sinθ.这种图形的变换可以作为柯西不等式的另一种几何诠释.这是本节课的遗憾之处.

2.进行选修教学评析，使学生善于探究

探究过程中通过提问的方式进行活动评析，确定探究方法、体会思想.探究过程的每一个环节：直角三角形的选择、用直角三角形拼四边形、从面积出发建立不等关系、不等式成立范围的讨论等等，几乎都在与不等式a2+b2≥2ab相类比.令学生对“类比”这一科学探究中的重要思想方法印象深刻，从几何直观入手的做法亦能使学生体会数形结合思想在研究不等式中的作用.课堂小结也是对探究活动的评析.总结探究时所运用的思想方法，并让学生学会提出问题，使他们善于探究.

公式的推导证明及向量形式部分耗时约25分钟，所以不等式应用环节意在让学生进一步熟悉柯西不等式，只安排了最基础的题型，没有过多地展开，应用部分将在下一课时重点教学.这样的安排不仅能较好地完成教学目标，使学生体验到探究的乐趣，还有助于学生形成正确的思维方式，培养他们发现问题、分析问题和解决问题的能力.当然探究能力的培养是长期的教学任务，不可能一蹴而就.这需要我们教师坚持不懈地反思自己的教学，明确怎样做才能有利于学生探究能力的养成，从而调整教学方法.

1.陈雪松.柯西不等式的教学实践及反思［J］.数学教学，2009（10）.

2.李广修.追求非功利化的数学教学［J］.中学数学月刊，2014（2）.G