深入挖掘 探寻课后习题的潜在功能

张建

习题对于高中数学教学来讲，既是课堂教学的重要组成部分，更是课后巩固所学知识的必备环节.虽然数学当中的知识内容都是通过课堂教学来予以呈现的，但是，课上时间毕竟有限，学生们只能完成对知识内容的初步接受，却无法从思维上深入接受并加以运用.可以说，课堂教学只完成了数学知识学习的一小部分任务，更重要的在于课后练习.因此，课后习题对于高中数学的意义不可小觑.对于课后习题加强关注，并深入挖掘出习题当中的每一分价值，更是高中教师应当思考的课题.

一、抓住跨学科习题，挖掘联系功能

数学是一门内容渗透十分广泛的学科，在生产与生活的每个角落都能够发现它的身影.因此，在很多情况下，数学知识都不是独立存在的，以数学方法解决其他学科内容的问题已经逐渐成为了一种常态.特别是在高中阶段的学习过程当中，这种跨学科的现象出现得尤为频繁.这也要求学生们不仅要学好数学知识本身，还要建立起与其他学科的联系意识.

例如，在完成对椭圆知识的教学后，我为学生们布置了这样一道课后习题：椭圆具有这样的光学性质：光线从椭圆的一个焦点出发，经椭圆反射后，反射光线必然经过椭圆的另一个焦点.现将一个椭圆形的台球盘水平放置，其两个焦点为点A和点B，长轴长是2a，焦距是2c.把一个半径忽略不计的小球从点A直线打出，当其经椭圆壁反弹后回到点A时，经过的路程是多少？经过对已知条件的分析，可以根据小球的不同运动情况得出4a、2（a-c）和2（a+c）三种答案.在这个过程中，学生清楚地看到了数学知识在物理背景中的应用.

在高中数学当中，经常会出现以其他学科内容为背景的习题，这些跨学科出现的问题，对于建立学生们的联系意识来讲很有好处.这不仅可以作用于数学学习过程之中，拓展学生们对于所学知识的应用范围，更可以作用于其他学科，以数学的思维帮助学生高效解答相应问题，实现数学与相关学科学习效果的同步提升，全面提升学生的综合能力，彰显数学学习的魅力.

二、抓住探究性习题，挖掘拓展功能

高中数学学习已经进入到了一个比较高级的阶段，它对学生的学习要求已经不再停留在知识本身，而是站在更高角度，对学生们的数学思维能力提出了要求.也就是说，学生们不仅要将基本知识理解清楚，还需要从中找到数学问题的思考方式，以之去解决更为灵活和广泛的新问题.单一的语言叙述很难将学生们的这种能力建立起来，借助习题是一个有效的途径.

例如，在学习过导数内容后，我为学生们布置了这样一道探究性习题：设函数y=f（x）的导函数f ′（x）=g（x），g（x）的导函数g′（x）在[a，b]上的值为负的充要条件是y=f（x）是凸函数（即函数y=f（x）的图象在[a，b]上均在其任一点的切线下方）.（1）求函数f（x）=x+cosx的凸区间；（2）若区间D上的凸函数满足性质：对x1，x2，…，xn∈D，恒有f（x1）+f（x2）+…+f（xn）n≤f（x1+x2+…+xnn），其中，当且仅当x1=x2=…=xn时等号成立，求证：在△ABC中，sinA+sinB+sinC≤323.这个问题具有很强的探究性，虽然难度不小，却是由既有的导数、不等式等内容拓展出来的，大大延展了学生们对所学知识的认知视角.

高中阶段的探究性习题数量不少，且经常被学生们视为“老大难”.这个类型的问题由于比较灵活和深入，解答起来难度较大.而也正是这个特点，若能把它运用得当，能够成为拓展学生思维广度的有力武器.

三、抓住实践性习题，挖掘应用功能

数学学习与实际应用之间向来存在着十分密切的联系.实际应用既是理论知识的一个重要表现形式，也是检验学生知识领会效果的有力途径.如果教师能够对一些典型的实践性习题加以挖掘，对于学生知识学习效果的提升将是很有助益的.

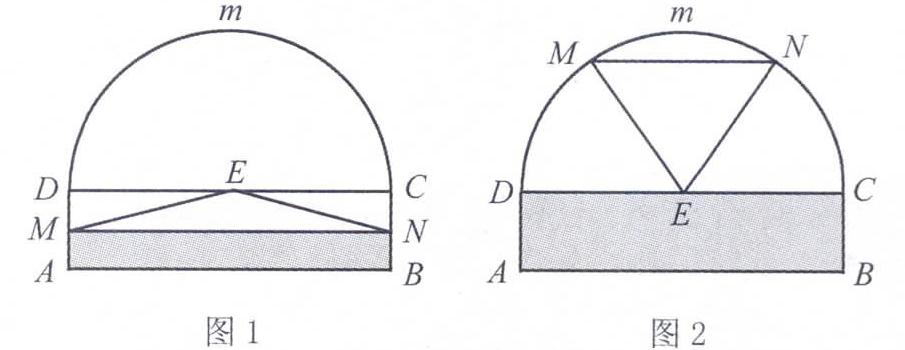
例如，在对函数内容进行复习时，我为学生设计了这样一道实践性习题：为保持仓库温度和湿度，墙上需安装如图所示的自动通风装置，装置下部ABCD是矩形，AB长2米，BC长0.5米，上不CmD是半圆，固定点E是CD中点.△MNE为三角形通风窗，可由电脑控制其形状变化，MN可沿边框上下滑动且始终与AB保持平行（MN与AB、CD均不重合）.那么，当MN与AB距离多少米时，△MNE的通风面积最大？通过解答这个问题，学生们真实地看到了函数知识在实际生活当中的有效表现，问题的应用功能也被成功挖掘出来了.

在高中数学的各类练习与测验当中，从来不乏应用问题的出现.这也警示我们，无论是从应试的直接角度考虑，还是从学习的长远发展来看，将数学知识投入到实际应用当中都是一个必为之策.教师在布置课后习题时，一定要树立起勤于应用的意识，打破“学什么，练什么”的狭隘眼光，让习题内容丰富起来，引导学生们在夯实理论基础的同时，将之运用到实际问题的解答当中去.这样的教学过程才是完成的，更是当前高中数学所需要的.

一道优秀的课后习题，其价值绝不仅仅表现在表层的练习过程上.对之进行深入挖掘，便可以发现运用该习题进行训练所能实现的理想效果.当然，这不仅需要教师善于发现的眼睛，还需要学生们勤于思考的头脑.通过本文的叙述便不难发现，高中数学课后习题的潜在功能是多种多样的，它随着习题的形式与内容的变化而变化.高中阶段的数学知识难度本就增加了许多，这对教师的教学开展提出了不小的挑战.如果能够抓住课后习题这一巧妙入口，在帮助学生巩固所学的同时，更能够为课堂教学提供有效补充.这对于教学实效的整体提升来讲，作用显著，值得每位教师予以关注和推广.