重视数形结合提高解题能力

朱庆

【摘 要】数形结合就是把抽象的数学语言、数量关系与直观的几何图形、位置关系结合起来，通过“以形助数”或“以数解形”，即通过抽象思维与形象思维的结合，可以使复杂问题简单化，抽象问题具体化，从而起到优化解题途径的目的，在数学教学中能够提高学生的解题能力。

【关键词】数形结合；数学解题；解题能力

数形结合就是把抽象的数学语言、数量关系与直观的几何图形、位置关系结合起来，通过“以形助数”或“以数解形”即通过抽象思维与形象思维的结合，可以使复杂问题简单化，抽象问题具体化，从而起到优化解题途径的目的，在数学教学中大大地提高学生的解题能力。

一、“数”向“形”转化，提高解题能力

1.“数”转化为“形”，提高证解不等式的能力

运用数形结合的思想，就是将抽象的数学语言与直观的几何图形结合起来，通过图形的认识和数形的转化，使问题化抽象为具体，最终使问题获解。

2.“数”转化为“形”，注意帮助学生提高解绝对值问题的能力

我在对绝对值部分教学时发现学生要把绝对值正确打开较难，我分析了一下原因：主要是学生只会想到代数中去绝对值的三种情况（当未知数大于0；当未知数小于0；当未知数等于0）如果纯粹用代数方法告诉三种条件中任意一种学生都能做对，但条件隐藏在几何图形或者数轴中时就做不对了；还有不会利用图像法解决绝对值的题。我在教学时教会找准绝对值中数与数轴中的点有一一对应关系就是契合点，一定要把数轴中的点表示数的大小关系、绝对值关系弄懂才是解对题的前提，另外用利用图像法可以解除学生对于绝对值的思维障碍，顺利的解决问题。

二、“形”向“数”转化，提高解题能力

1.“形”向“数”转化，提高解决函数问题的能力

在数学中，发现不少学生不会分析图形，正确认识图，更不会把图形数字化，模拟化，从而造成题不会解或解错，所以平常要注重培养学生识图能力，把形向数转化，使学生的解题能力得以提高。

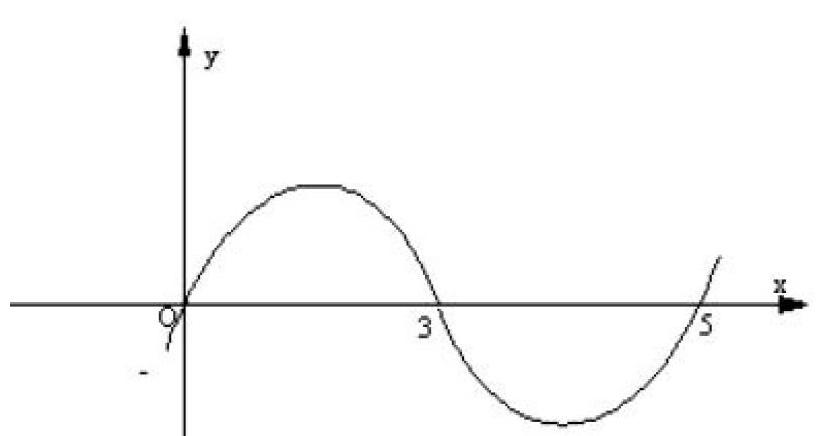
例：已知f（x）=ax3+bx2+cx+f 如图

求：b范围。

解析：设f（x）=ax（x-3）（x-5）= ax3+bx2+cx+f

∴b=-8a 由f（-1）=-a（-4）（-6）=-24a<0

∴a>0 故b=-8a<0

此例是典型的以形化数，由图形观察特殊点的函数值获取不等式，若学生没有较好识图能力和转化能力是不解决题的。可见培养学生形化数在解题能力培养方面的重要性。

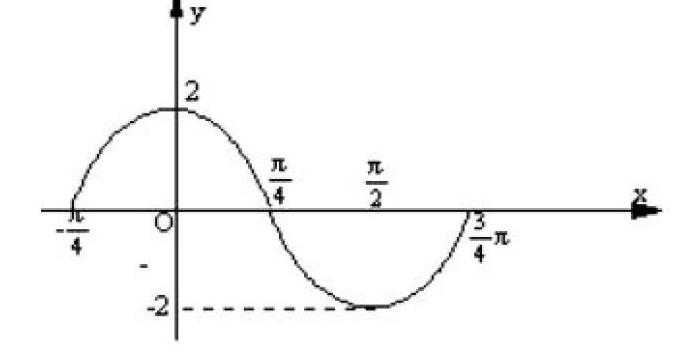
例：看图填空

函数y=Asin（wx+Q），则A= 2 ，周期T= π ，w= 2 ，Q= y= 2sin（2x+）

此例是由图形求三角函数解析式问题，此例不但要理解A、W、Q的作用，更要能识图，二者必须紧密结合，做到形与数的等价交换，方可快捷准确解题。

2.“形”向“数”转化，注意帮助学生提高解几何问题的能力

在平面几何教学时遇到一些几何题用学过的几何知识是没有办法解决的，不论用多少时间是无法做对的，学生如果掌握一些形转化为数的知识，对这类型问题就会迎刃而解，我在讲解时总是抓住几何的基本思想就是数形结合，在解题中善于将数形结合的数学思想运用于对有些图形太过于简单，直 接观察却看不出什么规律来，这时就需要给图形赋值，如边长、角度等。

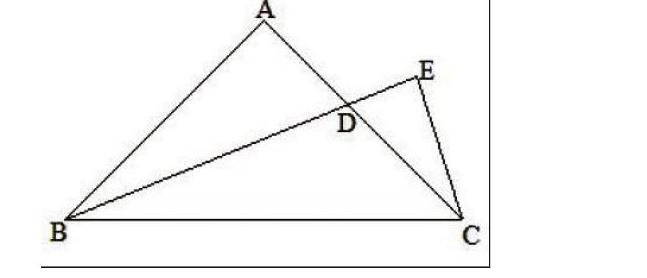
例 在Rt△ABC中，∠BAD=90°，AC=AB，BD是∠ABC的角平分线，CE⊥BE，求证：BD=2CE

解析：设AB=AC=a，由已知很容易得到∠ABD=22.5o，那么

BD= AD=atan22.5°

EC=（a-atan22.5°）cos22.5°

然后用BD除以AD，通过三角化简可得=2

通过图形数字化，并标在图上，易寻找二者的关系，用代数计算解决图形证明，做到形化数，在教学中只要牢牢地掌握这种形转化为数方法总会提高解题能力。形向数转化，可提高函数问题，几何问题的解题能力，没有准确的识辩图能力，不能有效把形转化为数，影响一些题的解决，只有很好做到形与数转化，使形与数形神兼备，才能很好提高学生的解题能力。

【参考文献】

[1]罗增儒.数学思维的一个案例——对两篇文章的再认识[J].中学数学教学参考，2003（1）：36-39

[2]陈皓.数形结合思想在《数列》教学中的应用[J].宁德师专学报（自然科学版），2004（4）

[3]初二数学教辅读物《学习指导》