绕曲线旋转母线长度不变性及其应用

高明海， 刘守鹏， 祁爱琴， 刘 琳， 刘 芳（滨州医学院公共卫生与管理学院，山东烟台264003）



绕曲线旋转母线长度不变性及其应用

高明海， 刘守鹏， 祁爱琴， 刘 琳， 刘 芳
（滨州医学院公共卫生与管理学院，山东烟台264003）

［摘 要］以椭圆曲线为旋转轴、平面曲线为母线，讨论母线保持长度不变性的旋转变换．首先，给出母线保持长度不变的条件、相关参数的取值范围以及参数之间的关系．其次，建立旋转变换模型．最后，以光滑曲线和折线为例，研究旋转变换的可行性及旋转模型的实用性，为折叠桌设计开槽曲线．

［关键词］母线；旋转变换；长度不变性；方程；参数

1　引 言

讨论绕曲线旋转的文献不多，研究此类问题的理论更少见．以曲线为轴的旋转变换涉及到旋转对象几何性状的变化，是空间旋转内容中较难处理的问题．2014年全国大学生数学建模竞赛B题［1］提出桌腿展开后可以与圆形桌面构成一张平板的平面折叠问题．截至目前相关文献很少，而且其中折叠桌设计方案都是取直线型钢筋连接桌腿且以折叠过程中钢筋起始位置和结束位置为边界开凿大面积槽口［2－3］，文献也没有涉及到曲线变换理论．

2　预备知识

2．1 符号说明与旋转假设

（i）参数a，b，L分别表示椭圆两个半轴长、矩形长边的一半；m，n，c为母线数据，H和h表示桌面高度和厚度，d表示桌腿旋转轴的量．

（ii）平面是由相互平行的一簇直线构成，直线不能弯曲；直线与直线之间可以弹性变化．

（iii）平板厚度不对旋转产生影响．

（iv）在推导过程中，旋转参数φ∈（－π／2，π／2）、椭圆参数θ∈（0，π／2）； φ（0）＜0，φ′（θ）≥0．

2．2 绕曲线旋转母线长度不变变换

在空间直角坐标系O－xyz中，有一个中心在坐标原点的椭圆

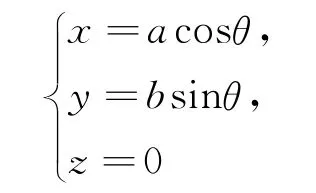
以及长为2L宽为2b的矩形．椭圆内切于矩形长边的中点，如图1所示．坐标平面xOy第一象限内存在一条以θ为参数的曲线MN，其参数方程为

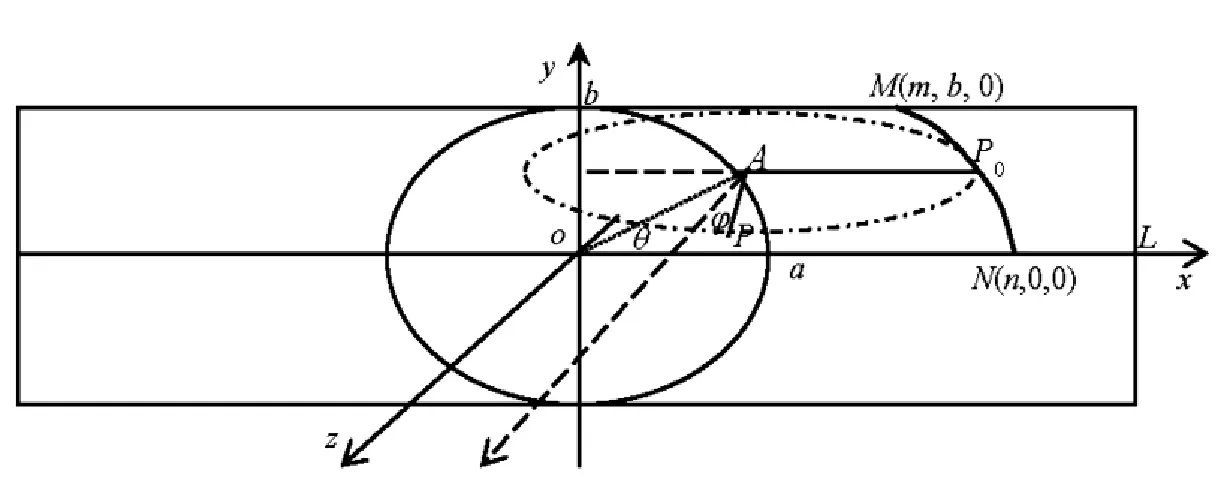
图1　曲线MN绕椭圆曲线旋转示意图

曲线MN上任意点P0与椭圆上点A具有相同y坐标，线段AP0绕A点旋转，P0终止于P，φ为AP与z轴的方向角．旋转终止时曲线MN对应的空间曲线为

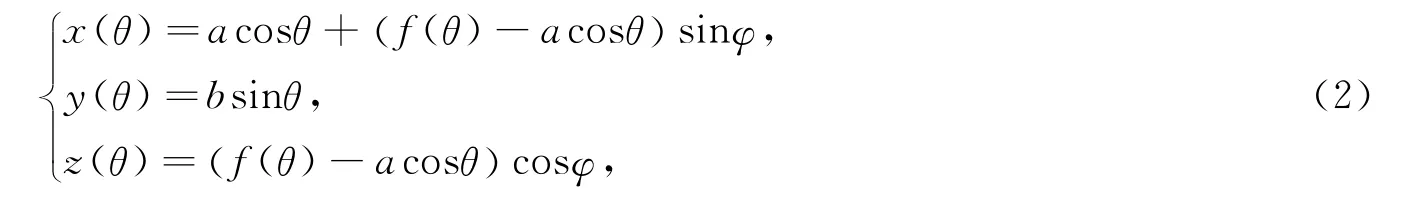
其中φ与θ具有关系φ＝φ（θ）．若旋转过程保持曲线MN长度不变，则式（2）满足

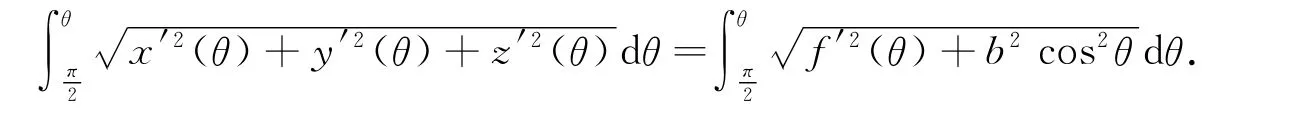
求导得

综合式（1），（2）和（3）得

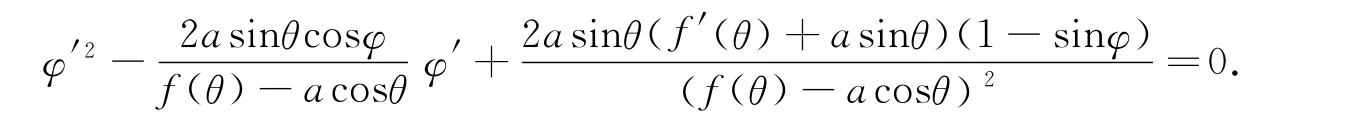
解得

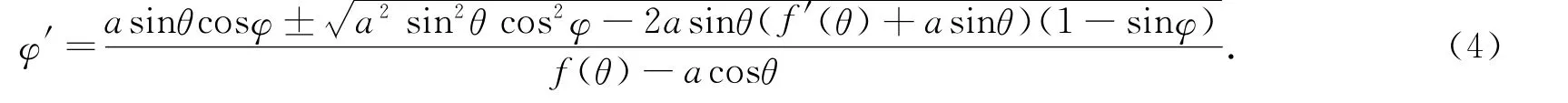
若要实解存在，由判别式大于等于零得

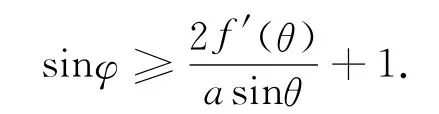
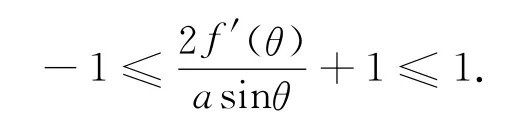
解不等式得到f（θ）的取值条件

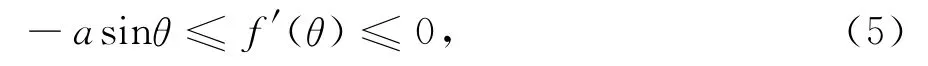
结合定积分性质，上式各部分分别在［θ，π／2］上积分得到

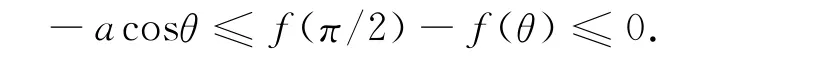
由f（π／2）＝m，得

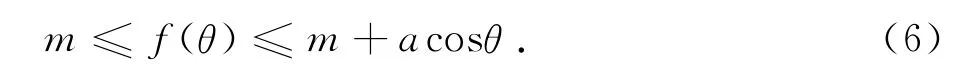
式（5）和（6）的几何意义如图2和图3所示，其中m可以小于a．式（6）有两种特殊情况．

情况1 当f（θ）＝m时，由式（4）得φ＝π／2，即直线MN的初始状态．

情况2 当f（θ）＝m＋acosθ时，

根据假设条件，若上式取大于号，得到f′（θ）＜0，则f（θ）存在范围宽泛；此处用取等号成立来限制f（θ）的范围，则有

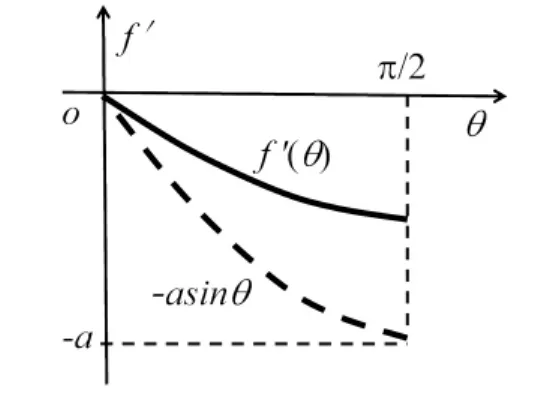
图2　f′（θ）的范围示意图

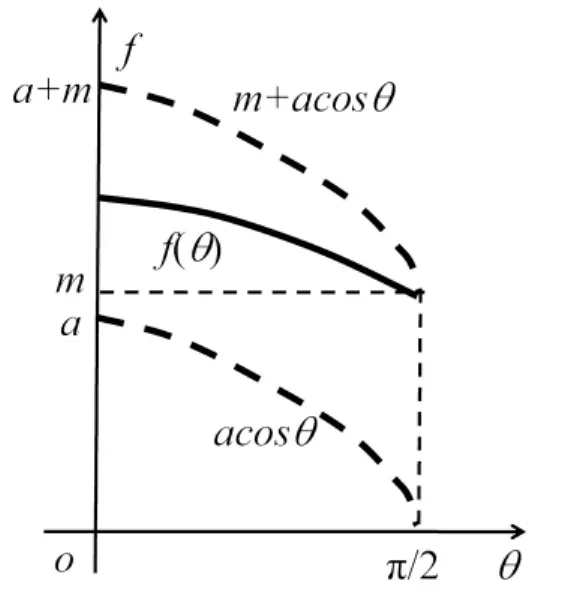
图3　x＝f（θ）分布示意图

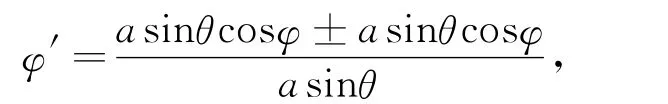
（i）分子取差．得φ＝φ0，φ0是由初始条件确定的任意常数，即旋转是自由的．

（ii）分子取和．φ与θ的函数关系为

其中C由初始条件确定．

除了两种特殊情况，f（θ）可以是满足条件式（6）由式（4）确定的任何连续曲线．

2．3 光滑曲线长度不变旋转模型

以端点M固定作为初始条件，曲线MN绕椭圆曲线旋转，保持长度不变须满足

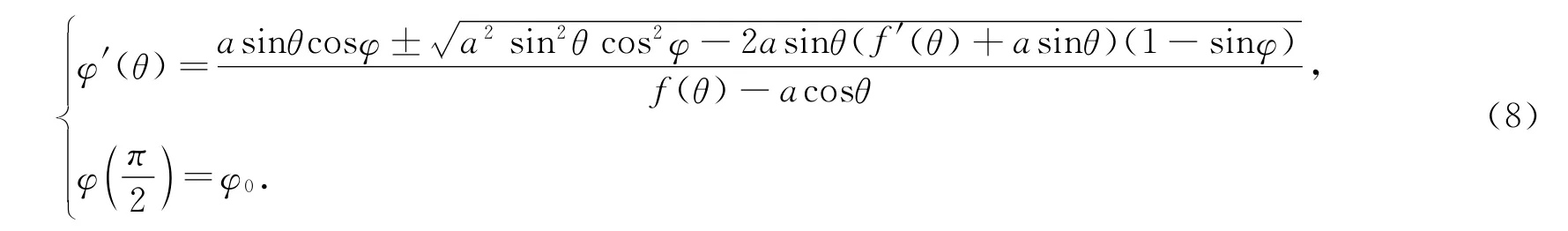
2．4 折线长度不变旋转模型

在实际情况下，由式（1）确定的曲线较难实现，取而代之的可以是整体形状与光滑曲线相似而局部差异较大的折线．根据式（5）得到

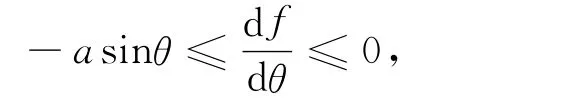
由式（1）得到

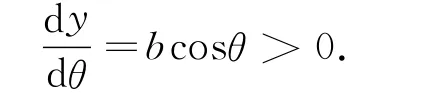
综合这两式，得

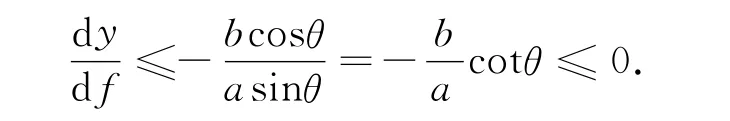
此式右端是椭圆上对应参数θ的点处切线斜率，即与椭圆具有相同参数θ的点处，折线MN的斜率不大于椭圆切线的斜率．如图4所示．

图4　折线MN上第1段旋转轴与第i＋1段示意图

k等分y的取值区间［0，b］．考虑到式（5）限制，令折线MN上i分点与i＋1分点连线斜率等于i＋1分点对应的椭圆上点处切线斜率－bcotθi＋1／a；由于k分点处相应斜率不存在，令xk＝xk－1．分点的横坐标递推公式为

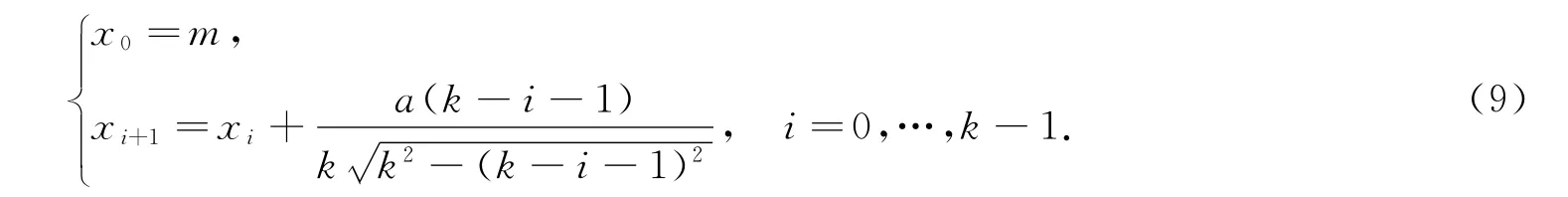
曲线换为折线，曲线旋转变换局部变成线段绕平面xoy内平行于y轴的直线旋转．折线旋转变换完

全由折线分界点旋转状态确定，记折线分段点处旋转角为φi＝φ（θi）．变换后的空间曲线由

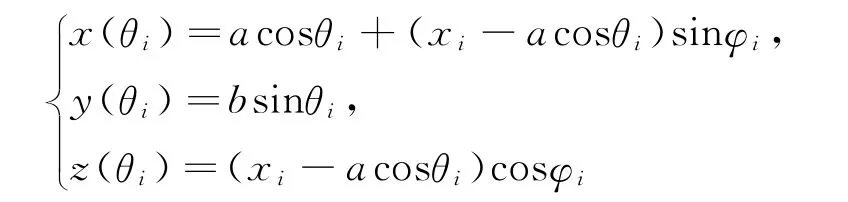
确定．保持长度不变变换的条件式（3）换为差分方程，即φi＝φ（θi）由

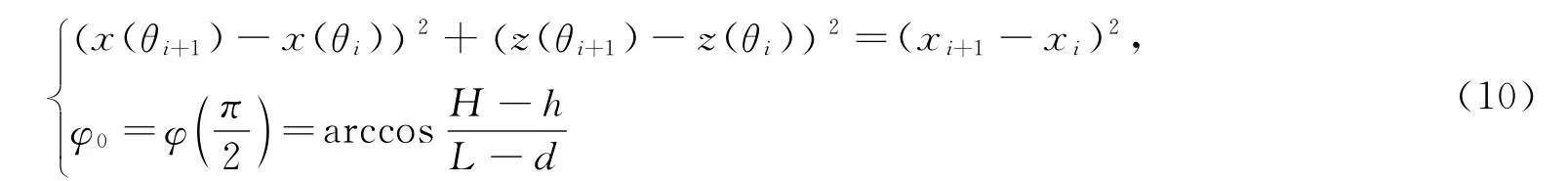
确定．折线的一段如图4所示，直线x＝d是第一段折线的旋转轴．

折线上不同的线段绕着不同的轴旋转，分段点既要满足前一线段旋转要求又要满足后一线段旋转要求，这种矛盾需要通过改变设计参数得以解决．如增加MN旋转自由度、旋转轴离散化为点等．

3　旋转轴为圆周的折叠桌模型

取参数L＝60cm，a＝b＝25cm，m＝30cm，H＝53cm，h＝3cm．可以验证，若式（4）中分子取和，则φ相对于θ的变化率太大即φ的取值范围过大，实际情况难以满足，下面仅讨论取差情形．

3．1 光滑曲线折叠桌模型

以光滑曲线f（θ）＝m＋ccosθ为例讨论．假设构成桌腿的窄木条足够多，木条绕点作中心旋转，中心都在圆周上．由桌高要求可以得到初始条件因此式（8）变为积分方程问题

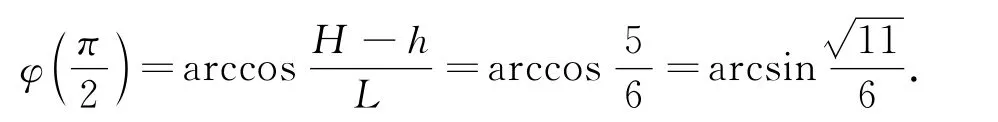
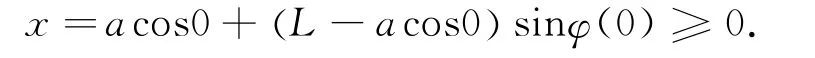
又因为折叠桌伸展平面关于y轴对称，其宽边中点旋转后的空间横x坐标不能小于零，即

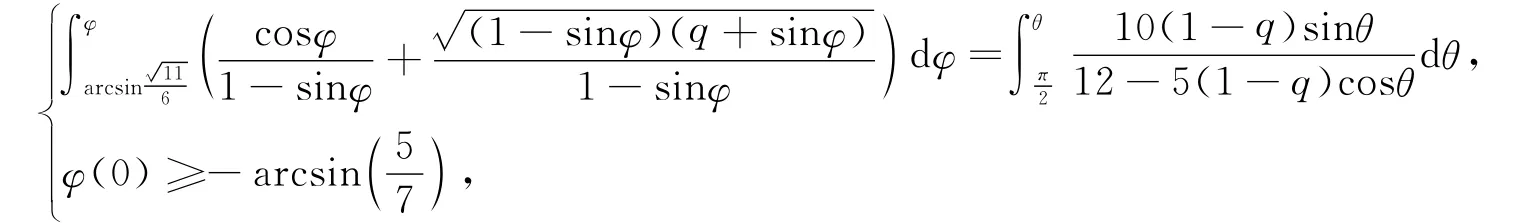
其中q＝2c／a－1．

积分方程右端积分上限θ等于零时，方程左端上限φ与参数q（或c）建立了函数关系．此问题只有唯一解q＝1（或c＝a）．若要得到其它解，可以通过优化参数L和c实现．

3．2 折线折叠桌模型

在实际情况下，连接桌腿的槽线呈曲线性状较难实现或造价高、呈平行于y轴的直线会造成桌面内槽太长；假设桌腿足够多且以点为中心旋转也是较为理想化的．比较切合实际的是MN为折线．根据式（9）取k＝10，可以得到折线MN的长度约为32．33cm，参数n＝46．90cm（此时折线比光滑曲线长约0．78cm）．其它相关参数，见表1第一、二、三行．

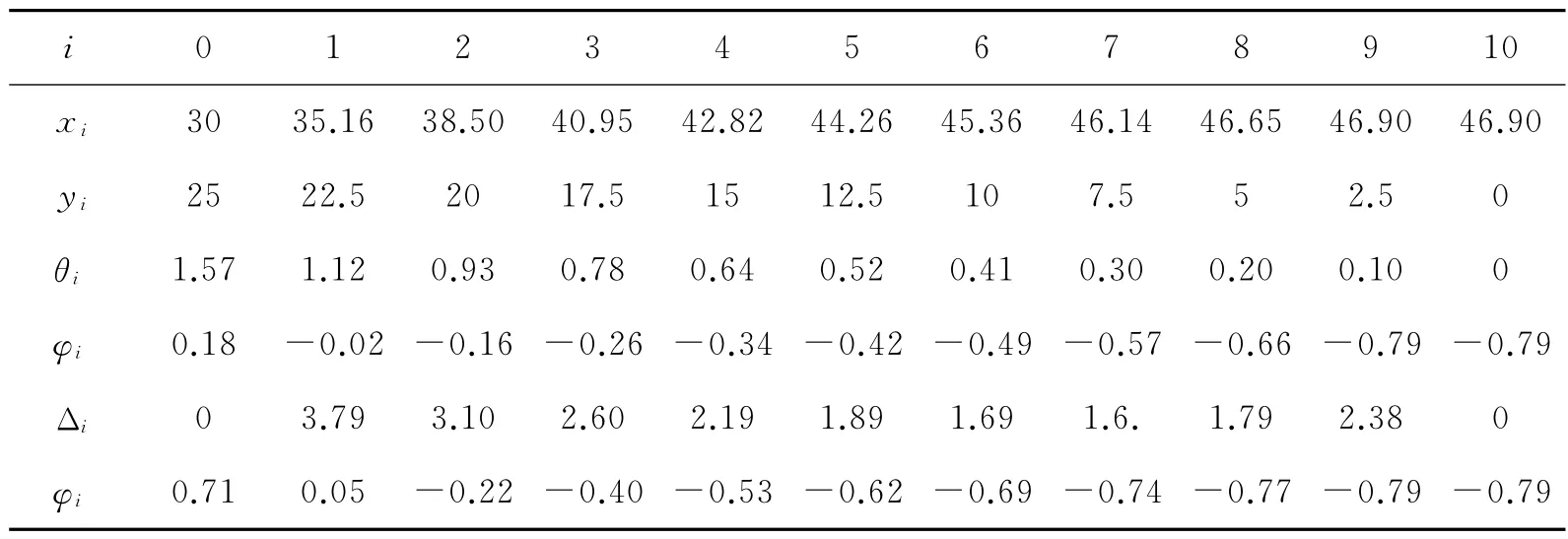
表1　折线分点坐标、内侧槽口长度（cm）和木条旋转角

木板对称性要求，其一侧宽边旋转结束时不能影响另一侧，即桌脚线中点横坐标x不为负：

此时旋转限制条件（10）变为

相邻折线旋转轴不同导致的矛盾，可以通过改善参数得以解决．方法是在每条桌脚宽木条的内侧开凿一定长度的线槽，也就是说把桌腿的每一宽木条槽口形状设计成喇叭形或三角形（如图5所示），以此保证位于同一分段点两侧的木条在旋转过程中其槽内槽线有足够活动范围，即给槽线增加一个自由度．活动范围即内侧槽口长度由桌面稳定折叠后相邻两木条旋转角φi与φi＋1的差异及其它相关参数决定．因为初始状态时相邻两木条对应的折线分段点重合，旋转变换导致位于两木条原本重合的分段点逐渐分离，分离长度Δ（θi）简记为Δi，如图5和图6所示．最后一木条（i＝9分点内侧）不需要扩大槽口．折线MN的i＋1分点对应的P0有两个旋转变换中心A 和A′，一个是相对于前一段折线，中心轴是x＝25cosθi（i≠0）；一个是相对于后一段折线，中心轴是x＝25cosθi＋1．同时，P0绕A（或A′）旋转变换后的P（或P′）点对应有两个旋转角记为φi（或φi＋1），其旋转轨迹在zox坐标平面的投影如图6所示，槽口形状见图5，槽口长度见图5和图6．

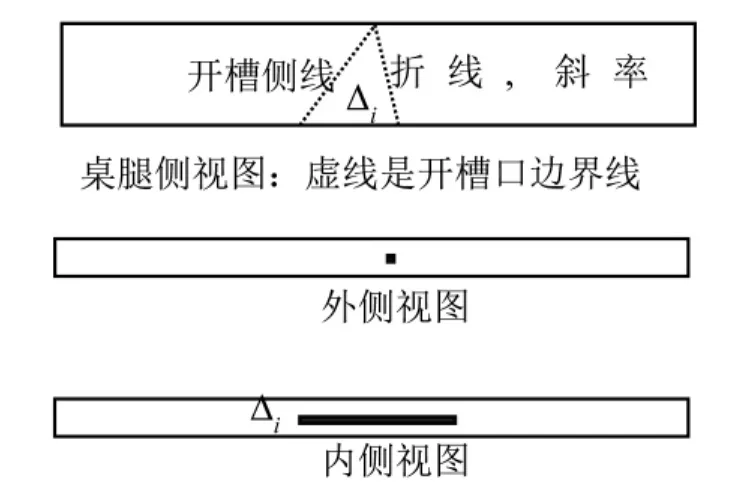
图5　桌腿宽木条开槽示意图

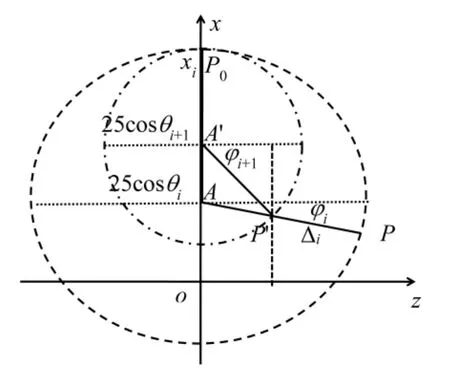
图6　折点旋转轨迹在zOx平面投影示意图

差分方程难以得到分析解，但可以换一个角度分析，根据图6得到关于φ的两个等式

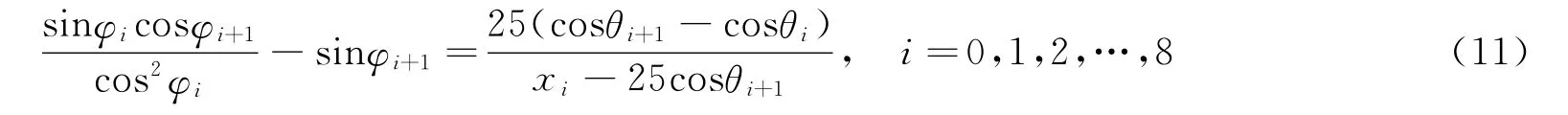
以及

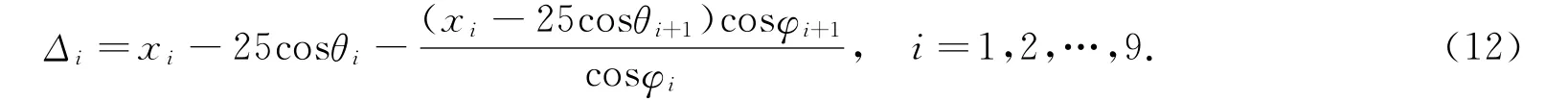
式（11）是差分方程的解．Δi与φi计算结果数据见表1倒数第二、三行．考虑到旋转终止条件，修正槽口长度和参数d．最后得到参数d≈9．16cm，旋转变换后曲线长度为30．40m．

桌体形状以及桌脚边缘的空间曲线图形如图7所示，桌脚线最高点距桌面和地面都是25cm，关于y轴对称触地桌脚相距约36．70cm，桌体稳定性较好．对称桌角线在最高点重合，便于借助外部部件固定桌体．

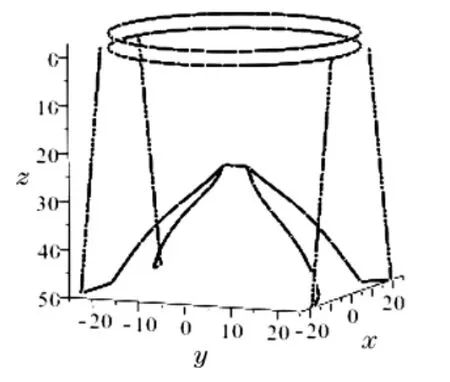
图7　桌体与桌脚线示意

3．3 模型参数优化

3．3．1 光滑曲线参数优化

若不考虑力学因素，桌体的稳定性需要考虑两个方面：一是对称桌腿底端距离不易太小；二是旋转结束状态稳定，可以通过外部构件使桌体宽边的中点重合在一起后借助外部附件实现，即满足φ（0）＝－arcsin［a／（L－a）］．实现的方法较多，如优化初始条件φ0、矩形长度L、位置参数m等等，也可以通过矩形宽边向内弯曲达到目的．此处只考虑优化矩形长度L，由式（8）得

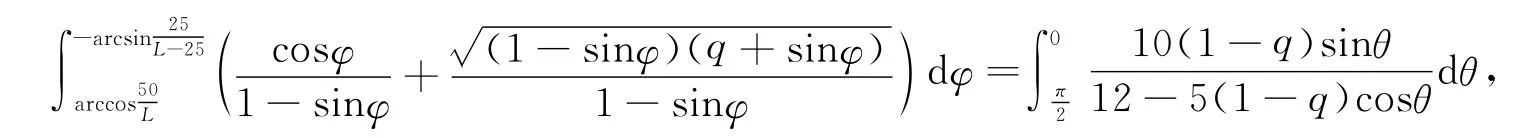
其中q＝2c／25－1，参数L和c的关系图形如图8所示．

只需取L＝59cm，c＝22．10cm即可．曲线MN的参数方程为

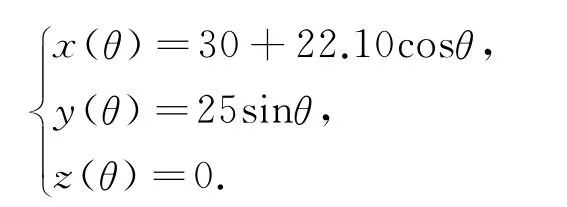
曲线端点N的坐标为（52．10，0，0）．此时折叠结果如图9所示，其中红色部分为桌脚线空间图形．

3．3．2 折线参数优化

折线模型的理论依据是光滑曲线模型，由以上讨论可知，可以进行参数优化．在桌高和板厚一定情况下，利用L与d的关系可以优化参数．根据式（10），取k＝10．即

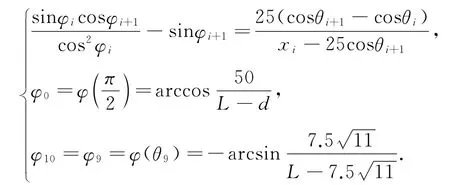
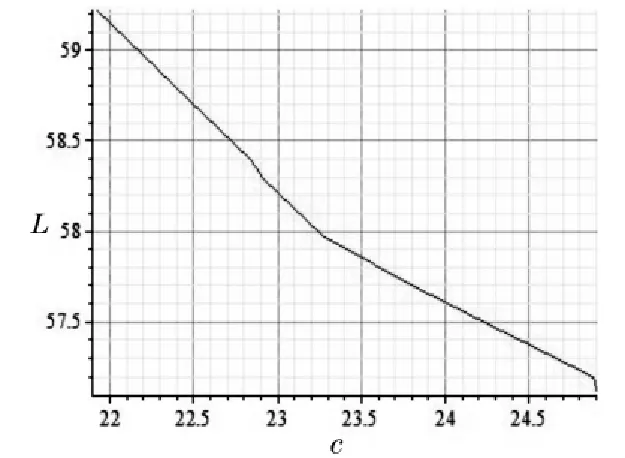
图8　L与c的关系图

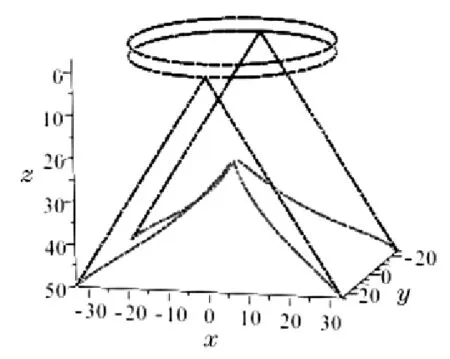
图9　红色为桌脚线空

虽然模型已知，但递推过程较长、运算过程难实现．此处讨论φ（0）恰好取到最小值时的情况，采用步长搜索［4］确定参数L的最优值，步长为0．5cm，数据见表2．

表2　参数优化（L与d的关系）步长0．5cm

根据需要取最优解，如L＝60cm，d≈1．35cm，图形与图7相似．

3．3．3 利用边界条件曲线优化

当式（6）达到最大值边界即f（θ）＝m＋acosθ时得到式（7），利用式（7）确定分段点把连续曲线离散化为折线，也可以实现参数优化．优化过程与结果如下：

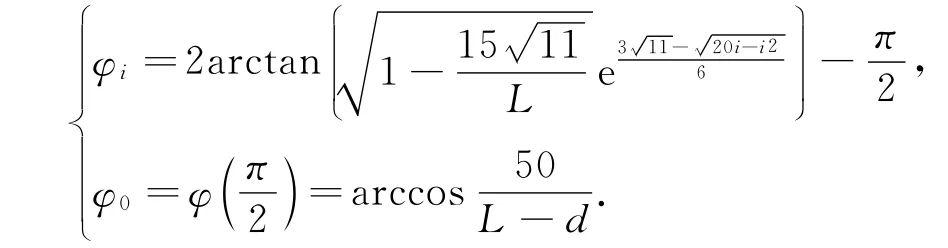
由此可以得到对应于参数θi的旋转参数φi，利用（12）也可得到数据Δi．在L＝60cm时，数据见表1最后一行．利用步长搜索法优化参数L和d，结果数据见表3．

表3　参数优化（L与d的关系）步长0．5cm

考虑到桌体的稳定性、美观性，两对称桌腿的距不能太小、d不要过小且尽量保证与其后两个旋转轴位置成单调数列，可以在表3中选取一对数值，如L＝57cm，d≈6．75cm．具体情况，可以根据实际需要确定参数值．对比两种优化参数d值，1．35cm牢固性差，6．75cm会更合理．

4　结 论

本文以椭圆曲线为旋转轴、平面内曲线为母线，研究在旋转过程中母线保持长度不变的变换，给出母线保持长度不变旋转变换应具备的条件、旋转参数的取值范围及参数之间的关系，建立绕椭圆旋转的分析模型．利用模型为折叠桌设计开槽曲线，并讨论了相关参数的优化设计策略．

在理论推导过程与模型数据检验过程中发现，参数之间的关系密切且变化率大．如参数c的较小变化量会导致φ有较大变化、d对L的影响也比较大、分段点确定方式对设计参数的影响较大．

［参 考 文 献］

［1］ 高教社杯全国大学生数学建模竞赛．B题：创意平板折叠桌，2014．http：／／www．mcm．edu．cn／problem／2014／cumcm2014problems．rar

［2］ 侯勇超，张大全，李媛媛，等．一种平板折叠桌的动态建模和最优设计［J］．巢湖学院学报，2014，16（6）：24－28．

［3］ 刘睿，张蒙，张政．创意平板折叠桌优化设计［J］．西安航空学院学报，2015，33（3）：65－71．

［4］ 高明海，刘守鹏．容器变位识别与容量表标定模型研究［J］．工程数学学报，2014，31（3）：321－340．

The Invariance of Length of a Generatrix Revolved about a Curve and Its Application

GAO Ming－hai， LIU Shou－peng， QI Ai－qin， LIU Lin， LIU Fang
（School of Public Health and Management，Binzhou Medical University，Yantai 264003，China）

Abstract：The rotation transform，with its axis is an elliptic curve and its generatrix is a plane curve，will be discussed，and the generatrixwill keep up its length in rotation．Firstly，the conditions of rotation，the range of parameters and the relationships between parameters will all be given．Secondly，the transformation model will be built up．Finally，the feasibility of the rotation transform and the practicality of the rotation model will be searched，and then the throating will be designed in the table legs，such as an elliptic curve and a broken line．

Key words：generatrix；rotation transform；invariance of length；equation；parameter

［基金项目］国家自然科学基金（11001117）；山东省教育科学“十二五”规划课题（YBS15019）

［收稿日期］2015－10－09

［中图分类号］O13；O172

［文献标识码］B

［文章编号］1672－1454（2016）01－0049－07