渗透核心概念落实课堂教学——《乘法口诀表的整理与复习》案例分析

莫国丽

义务教育《数学课程标准》（2011年版）给出“十个核心词”，即“数感、符号意识、空间观念、几何直观、数据分析观念、运算能力、推理能力和模型思想”以及“应用意识”和“创新意识”，也有专家认为它们就是学生在义务教育阶段数学课程中最应培养的数学素养。既然如此，教师应该以此为目标取向，通过一节一节课予以有效地落实。本文试以二年级《乘法口诀表的整理与复习》的教学实践为例，提出个人的一些思考，供大家讨论。

【过程1：出示课题，寻找九九表中的积】

师：今天我们要上一节复习课，在复习之前，老师想先知道你们对乘法口诀掌握到了什么程度。看屏幕，看得数说口诀。

（PPT逐一出示：2、10、40、7，学生逐一回答，同时教师逐一将积贴于乘法表格中）

师：（出示20）你们知道20贴在哪里吗？为什么？

（学生用手势指出20的位置）

师：四五 20（手势），原来20的位置和他的两个乘数有关系。

师：（出示15）请问贴哪里？为什么贴这儿？

师：接下来还有这几个数（48、63、21），分别应该贴哪里呢？请你用手对着表格指一指，他们分别在什么位置上？

（指名三个学生去表格上贴数字卡）

这个环节中，教师先让学生根据得数说出口诀，再一一将得数贴到表格中，学生观察、感悟制表的原理，了解九九表中积的位置跟两个乘数之间的对应关系，并进一步通过学生自己贴得数来作印证和巩固。一方面，这个过程本身是一个推理的过程，另一方面在这个推理的过程中，学生熟悉了表格的结构，为接下来的任务探索做好了准备。

【过程2：复习归纳积相等的口诀】

师：这是一张方格图，我在上面画了一些阴影。你能帮我算一算阴影部分一共有多少个小正方形吗？

生：一列有6个，一共有2列，2×6=12。

师：口诀是什么？

生：二六 12。

师：乘法算式可以怎么列？

生：2×6=12或者 6×2=12。

师：以6×2=12为例，你能说一说乘法算式各部分的名称分别是什么吗？

生：6是乘数，2是乘数，12是积。

师：还有哪句口诀的积也是12？

生：三四12。

师：可以怎么列式？

生：3×4=12或者 4×3=12。

师：问题来了：三四12，用阴影怎么画？

生：画3列，每列画4个。

师：还可以怎么画？

生：画4列，每列画3个。

师：由于老师的方格纸空间有限，选择其中一种方式画下来。画了4列，每列画3个。

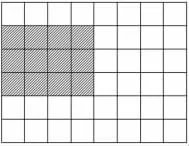
师：我们用阴影表示出了二六12和三四12，它们有什么地方是一样的？

生：积都是12。

师：我们把二六12和三四12称为一组积相等的口诀。

师：在我们的乘法口诀表里，你还能找到其他积相等的口诀吗？

生：四六24，三八24。

生：三六18，二九18。

师：请你好好想一想，在乘法口诀表里一共有多少组积相等的口诀？同桌之间互相交流写一写。

（一学生汇报口诀，另一学生根据口诀快速地将相应的积贴于九九表中）

师：好了，看起来同学们找得差不多了。我们数一数，一共有几组积相等的口诀呢？

生：9组。

师：通过我们的努力，得到了9组积相等的口诀。一起来读一读，记一记。

数形结合引出三四12和二六12，告诉学生像这样积都是12的两句口诀称为一组积相等的口诀，进一步展开合作与交流，引导学生有序地收集到全部9组积相等的口诀，并在乘法九九表中找到位置，强化记忆。

【过程3：归纳总结乘数相等的口诀】

师：刚才我们在方格纸里画了二六12、三四12，像这样根据口诀去画阴影图，你会吗？请你在表格里面先找一个自己想要的数，想一想你选的这个数所对应的口诀，并把口诀所表示的意思用画阴影的方式画在方格纸上。方格纸在练习纸的背面。注意：只要画阴影，口诀藏在心里就可以了。

（学生画阴影）

师：画好之后，去考一考你的同桌，问问同桌，我画的阴影所表示的口诀是什么？

师：我看到有些同学还画了一些很特殊的阴影，我把它们输入了电脑。大家一起看屏幕。这些图分别表示什么口诀呢？

生：一一得 1，五五 25，七七49，八八 64，九九 81

师：你们有什么发现？

生：这些口诀的乘数是相同的。

生：画出来的都是正方形。

师：看来乘数相同的口诀画出来的图形都是正方形的。你还能想到其他乘数相同的口诀吗？

生：二二得 4、三三得 9、四四 16、六六 36。

（屏幕展示从一一到九九的9个图）

师：你又发现了什么？

生：每次多5。

师：是吗？

生：每次多3。

师：是吗？每次增加的数一样多吗？

生：不是。

生：一一得1到二二得4，增加了3，二二得4到三三得9增加了5……

生：每次增加的数在不断变大，而且是有规律的。

师：数一数乘法口诀中一共有几句这样乘数相同的口诀？

生：9句。

（学生念口诀，教师将得数一一贴于表格中）

师：你们发现了什么？

生：乘数相同的数的积正好在表格的斜对角线上。

师：我们通过努力，又找到了9句乘数相同的口诀。

数形结合，丰富对乘数相同的口诀的理解，可以看成整体的正方形，也可以看成一层一层的增加，这是对乘法口诀极为贴切的几何直观。填入表格后又发现同数相乘的积正好位于一条直线上，渗透函数观念。

【过程4：寻找归纳积是反序数的口诀】

师：九九表中还有一些空白处，谁来帮我们填一填？

（学生练习纸上填九九表中剩下的积）

师：继续观察表格中的积，你还能找到哪些有特殊关系的数？

生：18 和 81。

师：特殊在哪里？

生：两个数的个位和十位反了一下。

师：我们把像18和81这样的称为一组积的个位、十位交换位置的口诀。像这样的口诀还有吗？

师：拿出练习纸，请你填一填像18、81这样积的个位、十位交换位置的数。

（指名展示：个位、十位交换位 置 的 积 还 有 27、72；45、54；24、42；36、63；12、21）

师：这次我们找到了几组积的个位、十位交换位置的口诀？

生：6组。

师：又找到了6组特殊的口诀——积的个位、十位在交换位置的口诀。

《数学课程标准》指出：创新意识的培养是现代数学教育的基本任务。学生自己发现和提出问题是创新的基础；独立思考、学会思考是创新的核心；归纳概括得到猜想和规律，并加以验证，是创新的重要方法。这一环节在前面活动的基础上，鼓励学生在九九表中自主寻找存在特殊关系的数，提供了创新的机会，培养了创新的意识。

【过程5：填写九九表，总结归纳】

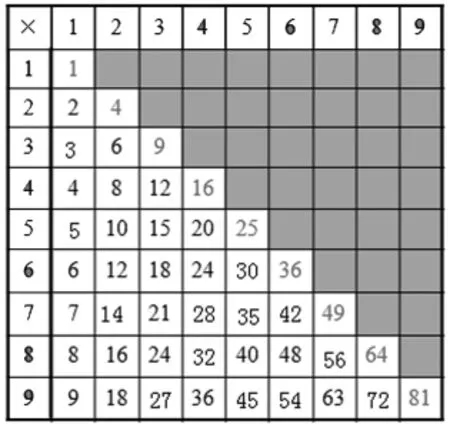
师：这个表格的灰色部分你会填吗？能填得又对又快吗？如果要填得又对又快，你有什么好方法？

生：心里念着乘法口诀。

师：还有比这更好的办法吗？想一想。先不说，我们比一比，看谁填得快。等下请最快的前10名同学来介绍经验。

师：1、2、……10，停！我相信你们都会填，那为什么有的同学填得那么快呢？我们请他们来介绍经验，好不好？

生：我发现第一行的答案就在第一列，第二行的答案就在第二列……

师：大家看屏幕，原来第一行的答案和第一列的答案是一样的。第二行呢？第三行呢？第四行呢……接下去是不是都是一样的？

师：啊，我觉得我们可以用一个词语来形容白色部分和灰色部分——

生：对称。

师：请问对称轴在哪里？

生：对角线。

生：就是正方形口诀（同数相乘的积）。

师：这节课我们复习了乘法的口诀，你印象最深的是什么？

生：我们整理了同数相乘的口诀，同数相乘的口诀在一条斜线上。

生：原来口诀不仅可以按1的口诀，2的口诀那样分，也可以按积相等、积的数字相反这样来整理。

把问题指向灰色部分积的最佳填写方法，引导学生关注表格的特点，培养学生观察、分析和推理的能力，提高思维的灵活性。