《两位数乘两位数》教学设计
章海燕
【教学内容】
浙教版三年级第60、61页。
【教学准备】
教师(大号红色记号笔)
学生(大号黑色记号笔,练习纸一张,展示卡一桌一张)
【教学过程】
一、导入
(播放学生测量篮球场的照片)
师:同学们还记得我们在做什么吗?
生:步测和目测。
师:是的!我们用步测和目测估计了学校篮球场的长和宽,还用卷尺测量了准确的长度。
(出示标准篮球场的图片)

师:我们一起走进体育馆,看看标准的篮球场。看图,你能提什么数学问题?
生:标准篮球场长28米,宽15米,它的面积有多大?
师:怎么列式?
(根据学生回答板书:28×15)
生:篮球场一排有23个座位,有19排,可以坐多少个观众呢?
师:怎么列式?
(根据学生回答板书:23×19)
师:观察这两个算式:28×15、23×19有什么共同点?
板书课题:两位数乘两位数
二、算法多样化:研究28×15的计算方法
1.学生独立思考,记录计算方法。
师:想办法算一算,你能想到几种计算方法就写几种,记录在练习纸第1题中。
(学生独立思考,记录计算方法)
(同桌交流:听一听同伴的方法,评一评对不对,好不好)
2.学生按要求学习,教师巡视、收集各种算法。
师:2人1组,把自己组认为好的方法记录在展示卡上,并贴到黑板上。
(提醒:每次贴时看一看,如果方法和已有的一样就不要往上贴了)
3.第一次归类。
师:同学们,你们太厉害了!想到了这么多种计算方法。为了方便交流,老师给每一种方法都标上序号。仔细观察这些方法,你能把它们分一分类吗?同桌可以商量一下。你们打算怎么分?依据是什么?


生:②和⑥为一类,其他的为一类。
师:你是怎么想的?
生:②和⑥是竖式的样子,其他都是递等式。
师:哦,原来你是看“样子”进行分类的呀!还有不同的想法吗?
生:①②④⑤⑨为一类,它们都把一个因数拆成两个数的和或差;⑦⑧为一类,它们都是把一个因数拆成两个数的积。③为一类,是估算;⑥为一类,是竖式。
师:听起来比只看“样子”要深入很多。
4.深入理解算理,评价算法。
师:先看第一类①②④⑤⑨。你有什么想说的?
生:我发现②和④完全一样,只是写法不同。你们看,都是把15分成10和5,分别计算28×10 和 28×5,再相加。
师:是这样吗?你们能结合篮球场的面积图来说一说这样计算的依据吗?

生:把篮球场的宽分成10和5,先算上部分的面积28×10=280,再算下部分的面积28×5=140,然后把这两部分面积相加280+140=420就是整个篮球场的面积。
生:其实就是乘法分配律。
师:(竖起大拇指)28×15=28×10+28×5,依据的就是——
生:乘法分配律。
师:那么①⑤⑨呢?
生:①也是乘法分配律。是把 28分成 20和 8,28×15=15×20+15×8。
生:⑤是把28分成30-2,也是乘法分配律。
师:同意吗?能到面积图上来解释一下吗?
生:先把篮球场的长看成是30,算出整个扩大后篮球场的面积,再减去多算的面积。

生:可以拆成和,也可以拆成差。
生:⑤拆的是28,⑨拆的是15,把15拆成了20和5的差。
师:(指两种方法)同意吗?
师:再看第二类。方法⑦和⑧该怎么解释?
生:老师我来画个图。28×5×3=420的意思就是把篮球场的宽平均分成3等份,先算出长28米宽5米的小长方形面积,3个就乘3。
生:15×4×7=420就是把篮球场的长平均分成7等份,先算出长15米宽4米的小长方形面积,再乘7。
师:我们现在分的这两类,依据是什么?
生:乘法分配律和乘法结合律。
(教师在相应的分类上板书乘法分配律、乘法结合律)
师:这就把“样子”不一样的算法背后一样的“道理”给挖掘出来了。老师为你们点赞。不过,我还想问问:这两类方法之间有没有一样的地方呢?
生:都把其中一个数进行拆分。
生:只不过一个拆成和或差,一个拆成积。
生:都是把我们还不太会算的两位数乘两位数,变成我们学过的、会算的几十乘几和几乘几。
师:把新问题转化成旧知识是了不起的数学本领。
师:再来看方法③,大家有新想法吗?
生:老师我觉得他上面写的是估算的答案,下面这个精确的答案和⑤一样。
生:对,③和⑤一样,也是把28算成30-2,应该归入“乘法分配律”这一类。
5.沟通竖式与其他算法的联系。
师:好,还剩下⑥。大家能看懂这个竖式的意思吗?先请这位同学自己来介绍一下。

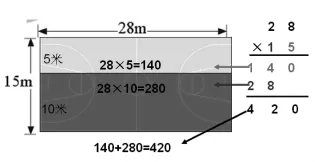
生:我用竖式算。先算个位上5×28=140,写在这里,再算十位上1×28是28个十,写在这里,最后加起来等于420。
师:照这样说,其实和我们刚才的哪种方法是一样的?
(根据学生的回答,取出对应的方法,并请学生在面积图上指一指)
生:那也就是说,竖式的根据也是乘法分配律。
生:⑥②④是一种算法的不同写法。
(学生鼓掌)
师:对,⑥是老算法,新写法。我们一起再来写写竖式。
(师生边对话边完成竖式板书)
师:第一步算什么?
生:28×5=140。
师:写在哪里?为什么?
生:140个1,末尾和个位对齐。
师:接下来算——
生:28×10=280。
生:只要写28就行了,末位和十位对齐,表示280。
生:十位上1×28是28个十,28的末位要和十位对齐。
师:最后——
生:加起来,等于420。
师:竖式的计算步骤大家都看明白了吗?有问题请举手。
三、算法一般化:研究23×19的计算方法
1.尝试计算 23×19。
师:刚才我们用这么多种方法算出了球场的面积是420平方米,现在我们一起来算算,这一部分观众席的座位到底有多少个?
(学生独立尝试,教师巡视、收集)
2.反馈。
投影展示四种不同的方法——
方法 1:23×(10+9)=23×10+23×9
方法 2:(20+3)×19=20×19+3×19
方法 3:23×(20-1)=23×20-23×1
方法4:竖式计算(略)
(教师分别统计:用这种方法计算的请举手)
师:为什么不利用乘法结合律来计算了呢?
(学生回答略)
师:看来遇到这样的数时,乘法结合律不适用,而竖式和乘法分配律却还是通用的。现在我们用通用的竖式来练一练。
(师生合作完成竖式)
师:(手指着竖式中“207”和“23”)哪个大?为什么?
生:下面的“23”是 23个十,也就是“230”,230>207。
四、总结
1.本节课中你对哪种方法的印象最深刻?
2.课外阅读资料:铺地锦的算法。

铺地锦原来是古代阿拉伯人计算乘法时用的一种方法,500多年前意大利的一本算术书中就讲述了这种“格子乘法”,后来传入我国,由于这种乘法的图式,很像用瓷砖铺的地面,故而得名“铺地锦”。

