由圆包络获取车轮磨耗曲线的算法研究
李静年,周文祥,李政璋
(1.西南交通大学 牵引动力国家重点实验室,四川 成都 610031;2.西南交通大学 机械工程学院,四川 成都 610031)
列车在行驶过程中车轮与钢轨相对滑动产生磨耗,为了能够检测钢轨或车轮磨耗后的断面曲线,一些接触式测量仪应运而生,包括丹麦绿林公司生产的Miniprof二连杆测量仪和牵引动力国家重点实验室研制的五连杆测量仪,其测量杆末端与测量轮连接,测量轮滚过被测对象,如钢轨轨头断面或车轮踏面外形。连杆机构带动编码器旋转,检测系统采集到角度数据。通过角度数据和数学模型只能得到测量轮的轮心坐标,要想得到被测对象断面曲线的坐标数据,还需要对轮心轨迹二维数组进行半径补偿。二维半径补偿的常用算法有测量方向补偿法、线线补偿法、二点补偿法和三点共圆补偿法等[1]。但是这些方法中采用了离散数组的数值处理方法(类似图像点处理方法),由于五连杆测量仪计算得到的离散轮心坐标数组量化误差较大,使用这些算法不尽理想。
考虑到求被测对象断面曲线(下文简称被测曲线)就是轮心曲线沿法矢方向偏移测头半径长度的结果,曲线拟合已广泛应用于测头半径补偿过程。文献[2-5]运用三次样条函数和二次曲面直接拟合轮心曲线,效果比较明显,但针对复杂曲面存在一定局限性。19世纪,Fourier得出任意周期函数都能展开成Fourier级数的结论。Fourier级数促进了偏微分方程理论的发展,成功解决了关于弦振动问题的解的争论;同时,Fourier级数是“信号与系统”课程的核心,也是处理科学和工程诸多问题不可或缺的理论工具。另一方面,Fourier函数拟合也被运用到各种实际问题中。文献[6]用傅里叶级数对客运量进行拟合与预测,得到了较好的效果。文献[7]利用Fourier级数时间序列模型拟合出自然灾害损失的变化趋势,并对未来5年内的情况进行了高精度的预测。本文也尝试用Fourier函数对车轮踏面曲线进行拟合。
1 轮心曲线拟合法
1.1 传统半径补偿方法
传统方法中采用两点法进行测量轮半径的补偿,如图1所示,已知测量轮中心C1、C2两个相邻点坐标,过C1作C1C2的垂直线与被测量的踏面曲线相交于O3,可得出△C1C2B与△C1O3C相似,从而得出点O3即踏面曲线上的点的坐标。
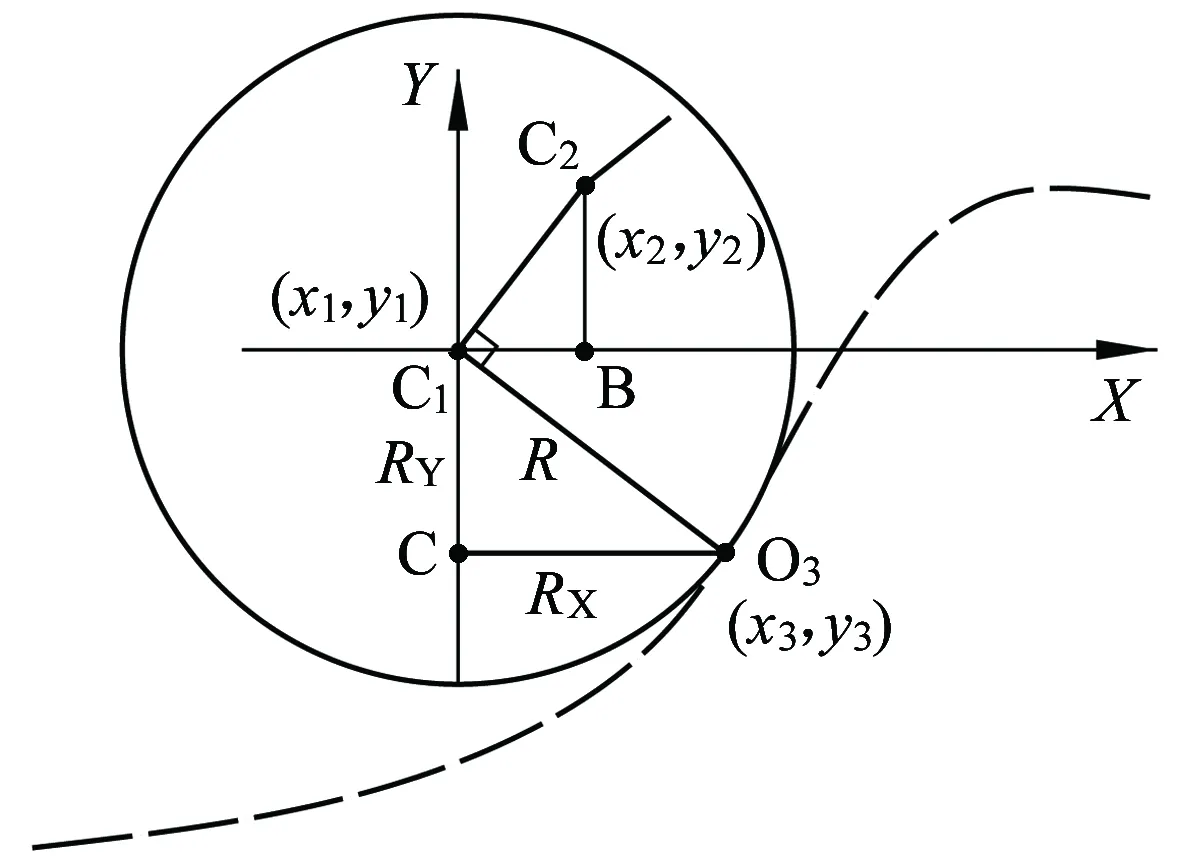
图1 测轮半径补偿
1.2 曲线拟合半径补偿方法
由于计算过程中只得到离散的轮心曲线坐标,在传统半径补偿过程中用差商代替导数值计算求出切点坐标(x,y)的值,此计算方法存在一定误差,而且编码器量化(取整)使数据产生局部趋势,数据整体不够平滑,半径补偿后的曲线容易出现自相交[8],同时也增大了测量数据的误差值。为解决自相交的问题,并进一步提高精度,尝试用曲线拟合的方法得到轮心的拟合函数曲线,用拟合函数的导数值计算半径补偿,求得被测曲线。
对于闭区间上的连续函数f(x),其Fourier展开若收敛必收敛于f(x)本身,即f(x)可以表示为
(1)
n=0,1,2,…,∞
(2)
n=1,2,…,∞
(3)
车轮曲线及其轮心曲线属于自由曲线。对于曲线拟合,拟合函数的选择影响拟合的结果,而对于任何闭区间上连续的自由曲线,其Fourier展开若收敛必定收敛于其本身[9],故考虑用n阶Fourier函数拟合轮心曲线。
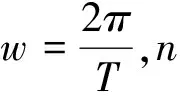
最小二乘曲线拟合中的度量指标向量的2范数达到最小[10],即
(4)
如果令
f=[f(x1)f(x2) …f(xN)]T
φi=[φi(x1)φi(x2) …φi(xN)]T
s=[s(x1)s(x2) …s(xN)]T
式(4)可化简为
(5)
在内积表示下
(f,f)-2(f,s)+(s,s)
(6)
由于
(s,s)=(a0,a1,b1,…,an,bn)·
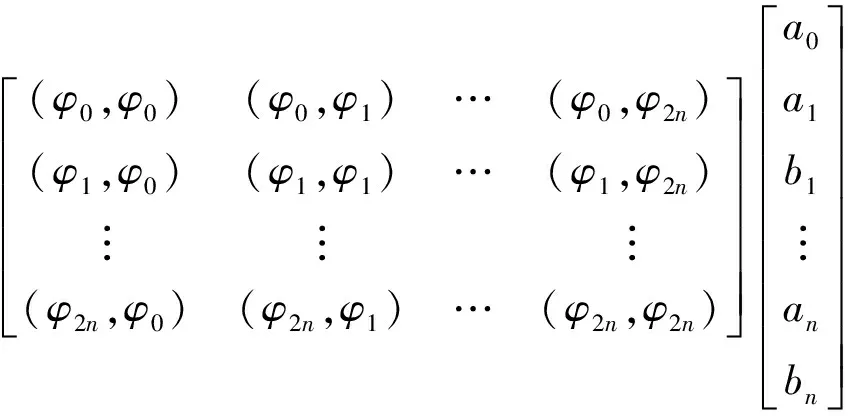
(7)
(8)
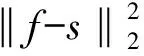
(9)
F(a0,a1,b1,…,an,bn)在R2n+1上连续,且存在偏导数。令各偏导为0,有
(10a)
(10b)
可得
(11)
求解出式(11)代入s(x)可以得到
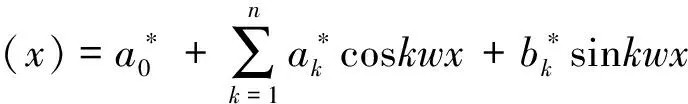
(12)
2 算例
为了能刻画出上文叙述方法所产生的误差,本文采用误差模型为:标准曲线偏移测量轮的半径长度得到轮心标准曲线,离散化获取一组轮心坐标,带入五连杆逆解模型,求得一组对应的编码器角度值,取整之后带入五连杆正解模型,得到一组轮心坐标。对这一组轮心坐标进行曲线拟合,并利用1.2节描述的方法求得拟合曲线包络,求得的包络即是实际断面曲线。通过比较实际断面曲线与标准曲线,计算法向误差。如图2所示。
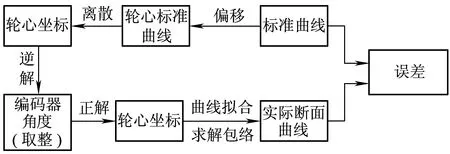
图2 误差模型
用MATLAB编出程序语言,以TB/T 449—2003《机车车辆车轮轮缘踏面外形》中JM3的几何标准曲线带入计算,为了提高拟合精度,减少计算量,将轮心坐标分成5段分别用8阶Fourier函数进行拟合。Fourier函数拟合的误差均维持为微米级,半径补偿结果如图3所示,计算误差如图4所示。用传统方法进行半径补偿得到的计算误差如图5所示。
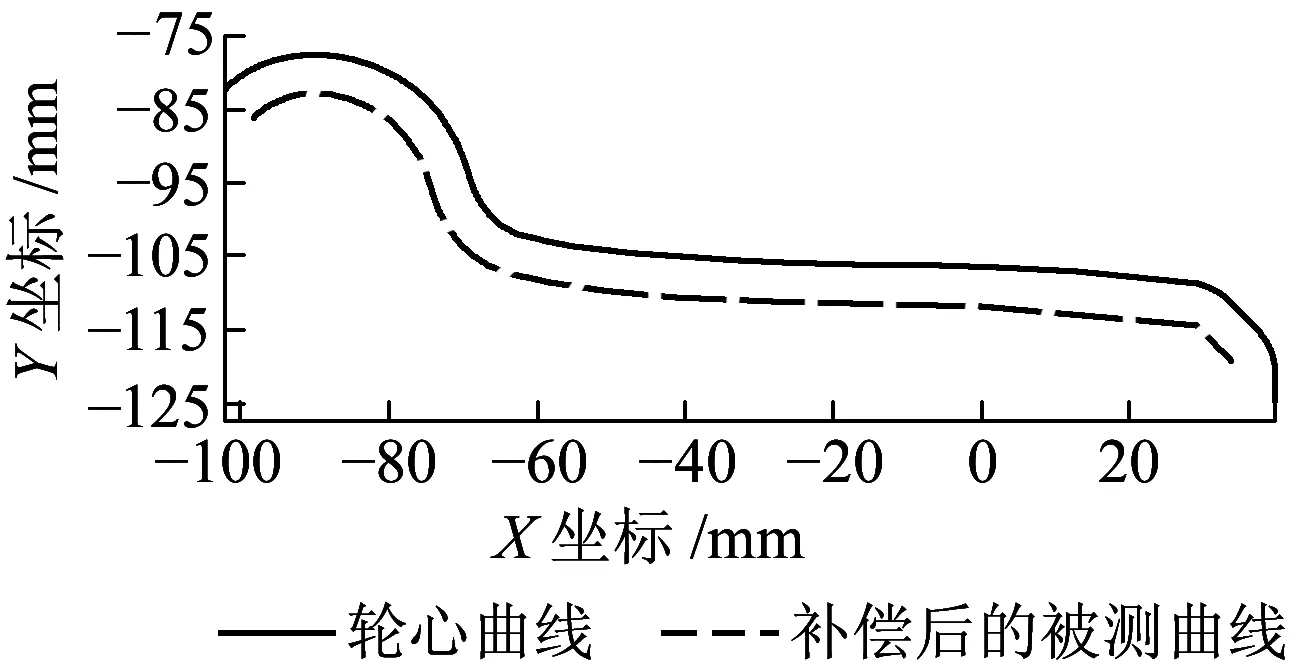
图3 曲线拟合半径补偿后的被测曲线
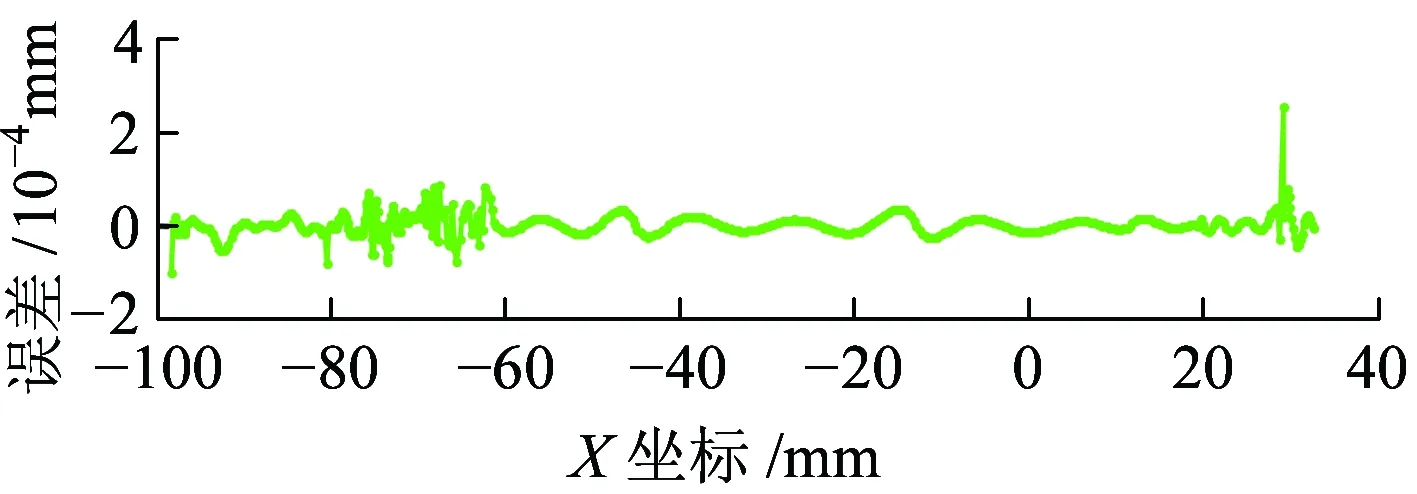
图4 曲线拟合半径补偿误差结果
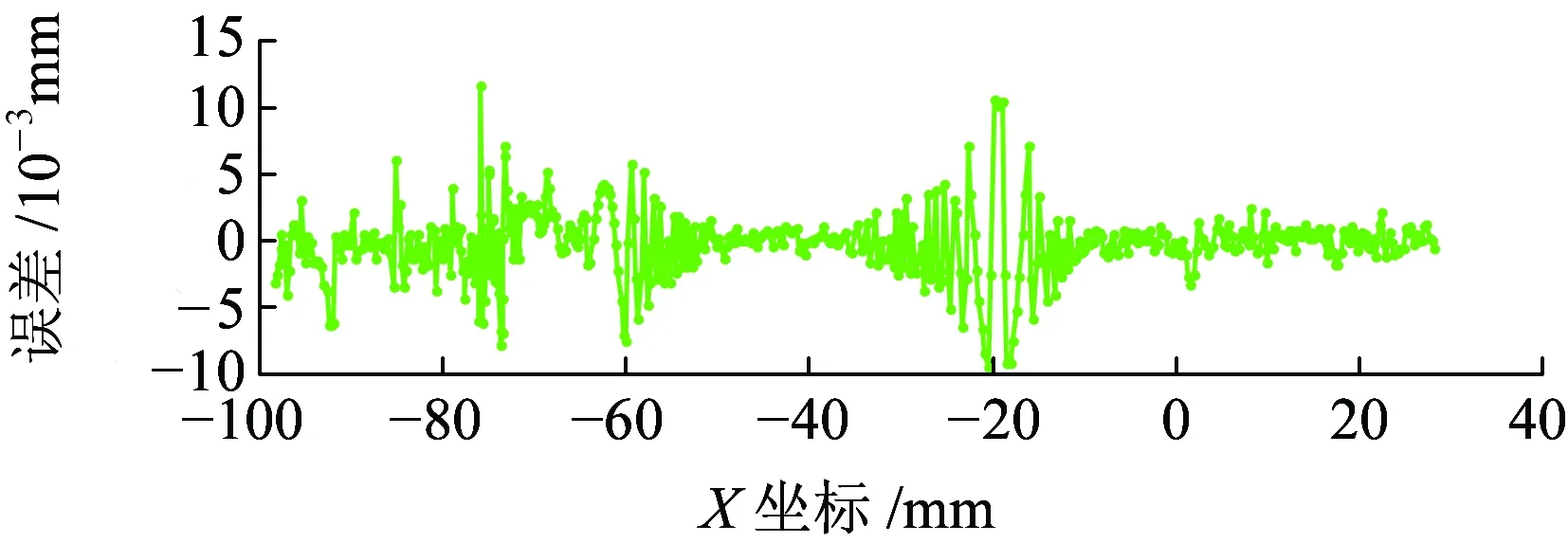
图5 传统方法半径补偿误差结果
误差结果显示,利用该方法所产生的误差绝对值小于3×10-4mm,在x=30附近误差相对较大,这是因为该点所对应的轮心曲线上的点处斜率发生突变,导致导数不连续。不过该点对结果影响不大。故被测对象具有较高的参考价值。
以下用Miniprof测量磨耗后的CRH5型车轮踏面的数据进行Fourier曲线拟合,如图6所示,拟合效果符合要求。
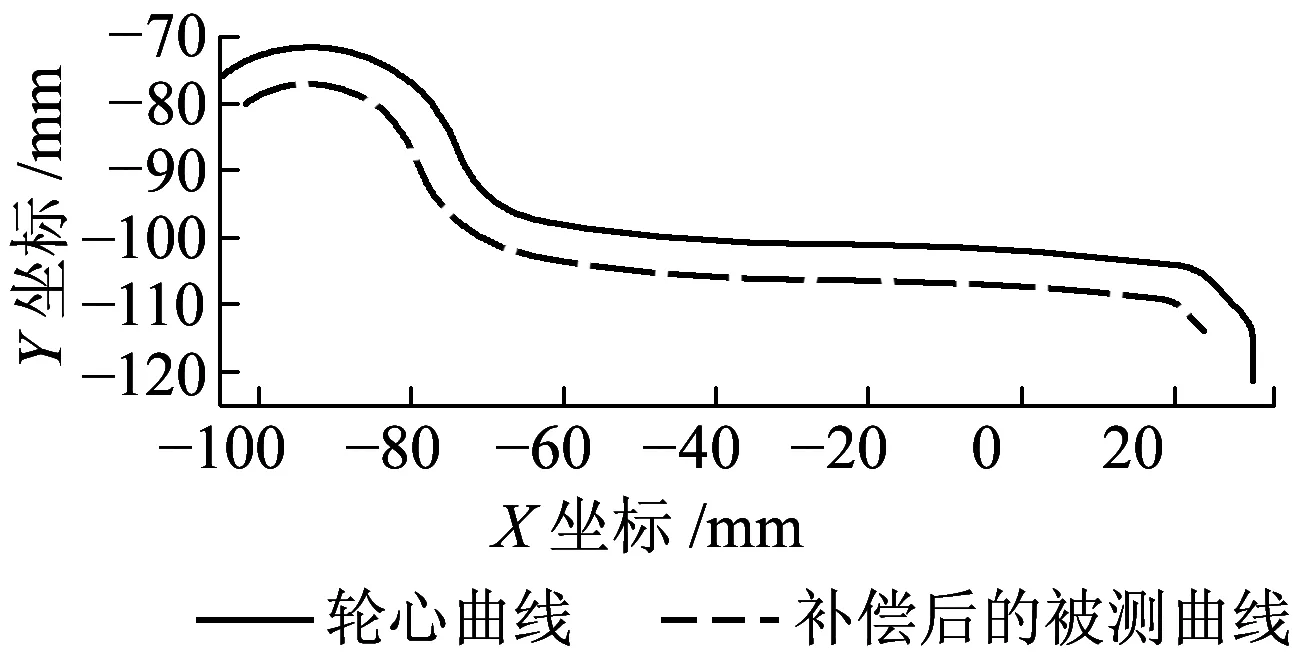
图6 曲线拟合磨耗后的车轮轮心曲线
3 结束语
由算例结果可知,采用本文的半径补偿方法,通过求解轮心拟合曲线包络的方式计算磨耗曲线能够较好地消除由编码器量化所产生的局部趋势,并减小由编码器量化和半径补偿过程带来的误差。并且该方法也成功拟合出磨耗后的车轮轮心曲线。本文采用8阶Fourier函数对由标准曲线经角度量化后得到的轮心曲线进行拟合,利用 MATLAB软件编程实现,拟合误差在微米级,通过求解轮心拟合曲线的包络得到实际断面曲线。与标准曲线比较,误差(法向距离)控制在微米以内。
参考文献:
[1]朱冰冰.便携式钢轨测量仪的改进及检验[D].成都:西南交通大学,2014.
[2]廖菲.基于CMM复杂曲面测量的采样方法及测头半径补偿研究[D].长沙:中南大学,2009.
[3]包园园.基于三次样条函数的自由曲线测量中数据处理方法研究[J].精密制造与自动化,2008(4):41-47.
BAO Yuanyuan.Research in Data Processing Method of Scribble Measurement Based on Cubic Spline Function[J]. Precise Manufaturing&Automation,2008(4):41-47.
[4]徐丽丽.接触式测头测量中测头半径补偿的研究[J].机械工程与自动化,2006(6):61-66.
XU Lili. Compensatory Method of Probe's Radius in Contact Measurement[J]. Mechanical Engineering & Automation,2006(6):61-66.
[5]许克凤.柔性测量臂测头半径补偿算法及平衡机构研究[D].武汉:华中科技大学,2009:42-47.
[6]于俊,陈国华.基于傅里叶级数的铁路客运量预测研究[J].铁道运输与经济,2011,33(2):92-94.
YU Jun,CHEN Guohua.Forecast of Railway Passenger Traffic Volume Based on Fourier Series[J]Railway Transport and Economy,2011,33(2):92-94.
[7]周长锋,龚日朝,肖国安.基于傅里叶级数的自然灾害损失预测模型研究——以湖南省自然灾害经济损失预测为例[J].中国安全科学学报,2009,19(8):5-9.
ZHOU Changfeng,GONG Richao,XIAO Guoan.Research on Natural Disasters Loss Prediction Model Based on Fourier Series: A Case Study of Human Province[J].China Safety Science Journal,2009,19(8):5-9.
[8]尼古拉斯M.巴利卡拉克斯.计算机辅助设计与制造中的外形分析[M].叶修梓,译.北京:机械工业出版社,2004:293-316.
[9]陈纪修.数学分析(第二册)[M].2版.北京:高等教育出版社,2004:405-425.
[10]徐跃良.数值分析[M].成都:西南交通大学出版社,2007:55-88.

