多绕组调节模式下变压器式可控电抗器工作绕组电流计算及其谐波分析
柳轶彬,田铭兴,赵茜茹,尹健宁
(兰州交通大学 自动化与电气工程学院,甘肃 兰州 730070)
电气化铁道供电方式特殊,负荷运行条件复杂,铁道无功负荷变化范围宽,波动大,冲击性与随机性强[1-2]。近年来,我国高速电气化铁路的建设规模不断扩大,需要性能更高的无功补偿装置对牵引供电系统进行无功补偿以提高其功率因数[3-4]。传统的固定电容器FC(Fixed Capacitor)、晶闸管投切电容器TSC (Thyristor Switched Capacitor)不能平滑调节输出无功[5-6];静止同步补偿器STATCOM(Static Synchronous Compensator)虽然调节性能良好,但维护困难、造价高[7]。相比之下,可控电抗器配合固定电容器[8]能平滑调节无功、响应速度快、投资少、见效快、可靠性高,是电气化铁道中比较理想的无功补偿方案;而选用性能良好的可控电抗器则是实施该方案的关键。目前电气化铁道无功补偿中的可控电抗器主要采用晶闸管控制电抗器TCR(Thyristor Controlled Reactor)和磁饱和式可控电抗器MSCR(Magnetically Saturated Controllable Reactor)[9-10],但二者的共同缺点是均会产生较大的谐波电流。
变压器式可控电抗器CRT(Controllable Reactor of Transformer Type)是一种能大范围快速平滑调节输出功率的无功补偿设备[11],特别适用于电气化铁道电力机车运行方式多变、负荷变化快的特点;与MSCR相比,其响应速度快且运行时噪声小;相比TCR,其谐波含量较小;与STATCOM相比,其制造成本低而且运行可靠,将其与固定电容器配合将是解决目前电气化铁道动态无功补偿问题的一个理想方案。
文献[11-13]对CRT的基本理论问题进行了详细研究,文献[14]对包括CRT在内的多种可控电抗器进行了系统地总结分析。但文献[11-14]的分析均只限于一个控制绕组处于调节状态。仅让一个控制绕组处于调节状态,控制策略简单,但其谐波含量不可控,而且在某些工况下仍然较大;事实上,CRT各控制绕组均可处于调节之中,满足同一个输出容量的触发角组合远不止一种,而工作绕组的谐波电流在不同的组合下却差异很大。因此,有必要研究CRT工作绕组电流的各次谐波有效值与各控制绕组的晶闸管触发角之间的定量关系,这对于优化CRT的谐波含量,提高其补偿性能具有重要意义。
基于以上目的,本文定义触发角向量,规定标准/非标准触发次序,引出多绕组调节模式的概念。采用分段线性化的办法求得CRT工作绕组电流在各时间段上的瞬时表达式。求出工作绕组电流各次谐波分量傅里叶系数与触发角向量的多元非线性函数的矩阵表达通式,进而给出基波与谐波电流有效值的计算公式。设计算例,验证了本文所给计算公式的正确性。
1 多绕组调节模式
CRT是一种对外等效电抗能在大范围内快速平滑调节的可控电抗器,将其与FC并联于牵引变压器的二次侧便可对牵引供电系统进行动态无功补偿,其基本原理如图1所示。
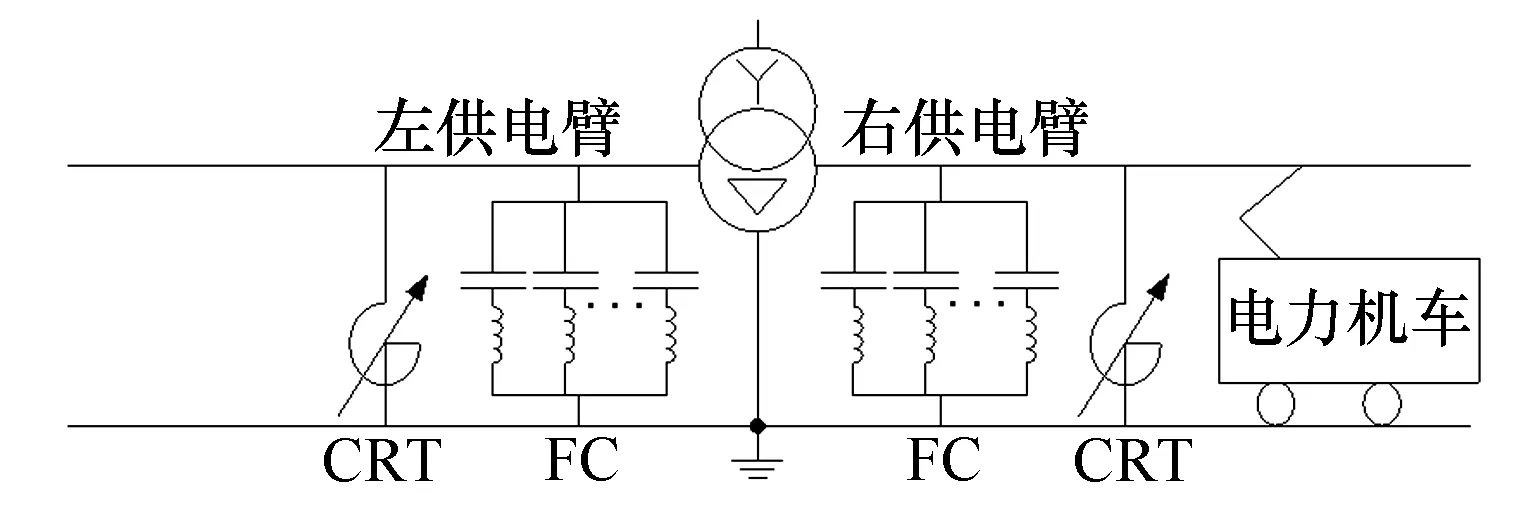
图1 CRT与FC的综合无功补偿示意图
图1中FC由若干个电容支路并联而成,且每条支路还串联一特定取值的电感,通过谐振可滤除特定次谐波电流(以抑制奇次谐波为主,主要为3、5、7频次谐波)。总体来看,FC能产生固定大小的容性无功;而CRT可发出介于其空载与满载之间的任意大小的感性无功;牵引负荷无功一般呈感性,其变化范围较大。因此,若采用合理的控制策略,在机车运行时的任一工况下,通过对CRT各控制绕组晶闸管触发脉冲的相位进行控制,使其产生的感性无功总能与FC发出的容性无功及牵引负荷无功相平衡,即三者之和始终接近于0,整个牵引供电系统的功率因数便能始终维持在接近于1的水平,可以提高机车的运行效率。
以上内容说明了CRT进行无功补偿时的应用环境,接下来,介绍CRT的工作原理,并引出多绕组调节模式的相关定义。CRT的电路原理如图2所示,图中W1表示工作绕组,与固定电容器一起并接在牵引变压器的二次侧;W2,W3,…,Wn为n-1个低压控制绕组;u1为W1的端口瞬时电压。
图2所示CRT为一台各低压控制绕组均串联了TCR的高漏抗多绕组降压变压器,其中T2,T3,…,Tn及X2,X3,…,Xn分别为各TCR所对应的反并联晶闸管及串联电抗(本文中称为限流电抗)。CRT采用高漏抗降压变压器,一方面具有降压隔离的作用,相比直接将TCR并联在高压牵引母线上,不仅可降低各反并联晶闸管的耐压等级,而且能隔离牵引母线的故障,提高设备可靠性;另一方面,各绕组较高的漏电抗可直接充当电感元件进行无功补偿,能减小各绕组所匹配的限流电感。
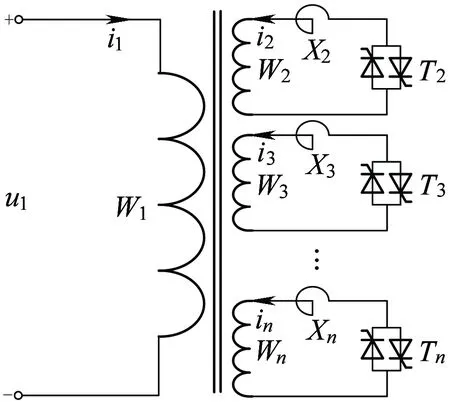
图2 CRT工作原理图
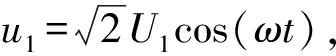
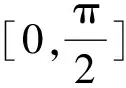
(1)α1≡0,表示工作绕组W1的触发角始终为0。虽然实际CRT的工作绕组W1中并没有串联晶闸管,但这里假想给工作绕组也串联了一个始终全导通的反并联晶闸管。这种处理并不改变CRT原有的工作原理,却非常有利于后文中公式的统一表示。
(2)除α1的下标始终是W1的编号外,αn其余各元素的下标不一定是图2中剩余各绕组的编号。αk(2≤k≤h≤n)对应第k-1个导通的控制绕组而不一定对应Wk,也就是说αn各元素下标代表的是相应控制绕组的触发次序,下标越小说明相应的控制绕组越先导通。
(3)αh之后再没有晶闸管导通,即αh+1=αh+2=…=αn=π/2。也就是说,共有h个绕组(包括工作绕组)在该工频周期里参与了运行,而另外n-h个(控制)绕组则始终处于截止状态。
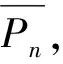
按照上述规定,在CRT从计时零点算起的任意一个工频周期里,任何一个控制绕组均有可能处于调节之中,处于调节状态的控制绕组的个数可以超过一个,可将其称为多绕组调节模式。
2 工作绕组瞬时电流分段表达式
为方便公式推导,对后文将会出现的各物理量进行说明(如无特殊说明,后文各物理量的下标意义均以此为标准)。
Lk(1≤k≤h≤n)表示αn的元素αk对应的绕组(不一定是Wk)的自感系数,Mkq表示αn的元素αk和αq(1≤q≤h≤n)对应两个绕组间的互感系数。Lxk为αk对应的绕组所串联的限流电抗器的电感系数(工作绕组没有串联限流电抗器,因此Lx1≡0),ik表示αk对应绕组的电流瞬时值。忽略铁芯饱和引起的非线性及所有电阻。
由于CRT工作绕组电流波形在正半周期里关于ωt=π/2对称,因此只须计算[0,π/2]时段上的电流表达式即可知道正半周期的电流波形。
按照第1章中关于多绕组调节模式的一系列规定,在[0,π/2]上,参与调节的h个绕组将按照αn中各自触发角的大小依次导通,因此,CRT的电路结构会随着各晶闸管的顺次导通而发生变化,也就是说,在[0,π/2]时段上,CRT的电路拓扑是非线性的;但是在相邻两个触发时刻所形成的小时段内,CRT的电路结构则是确定的线性电路。
根据以上分析,可以采用分段线性化的办法,将[0,π/2]时段按照当前周期的触发角向量的触发次序分成h个小时段,逐段求解,便可得到CRT工作绕组的瞬时电流在[0,π/2]上的表达式。
根据αn的定义,在第s(1≤s≤h≤n)个时段(αs,αs+1]上,总共有s个绕组在该时段上是导通的,于是有如下微分方程组成立
Ls(pis)=us
(1)
式中:p=d/dt;is=[i1si2s…iks…iss]T,其中iks(1≤k≤s)表示ik在(αs,αs+1]时段上的瞬时值;us=[u10 … 0 … 0]T;Ls为Ln的前s行s列子矩阵,而Ln是一个由CRT各绕组间的自、互电感及限流电感共同来决定的n阶方阵,称为综合电感矩阵,矩阵中各电感的下标意义与本章开始所述保持一致,Ln可以表示为
(2)
由式(1)可得
(3)
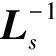
(4)
要求解式(4),须给定当前时段的初值,而当前时段的初值是上个时段的终值,由于第一个时段(α1,α2]的初值总是已知的(i11|ωt=α1=0),因此采用递推的办法便可求得[0,π/2]上任意(αs,αs+1](1≤s≤h≤n)时段上工作绕组电流的瞬时表达式,整理化简后,可将其表示为
(5)
式中:Vs=(0,E)-(E,0),其中E为s阶单位矩阵,0为s×1零向量;Cs=[x(α1)x(α2) …x(αs)x(ωt)]T,其中x( )=sin( );ys=[1/L1,11/L1,2… 1/L1,s]。
由于式(1)中的Ls(1≤s≤h≤n)是取Ln的前s行s列的子矩阵,而当触发次序确定之后Ln就是确定的,因此,各个小时段所对应的Ls总是确定的,从而各个小时段上CRT工作绕组电流的瞬时表达式便是唯一的。
式(5)给出了CRT工作绕组电流在任意(αs,αs+1]上的瞬时表达式,形式简单,便于后续公式推导,但并不直观。通过式(5)的展开式可知,CRT工作绕组电流在任意(αs,αs+1]上的瞬时表达式为
(6)
(7)
(8)
式(6)说明CRT工作绕组在任意(αs,αs+1)上的电流波形可由第s级临界波形直接平移而来,而平移的距离等于第1~s级差距之和。因此,当某个周期里各控制绕组的实际触发角确定之后,可确定各级临界波形以及各级差距,将相应的临界波形进行特定平移来逐段确定CRT工作绕组的电流波形,而无需重新分段计算。
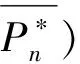
(9)
式中:Q为n阶方阵。若用qij表示其第i行第j列的元素,则qij的取值为
(10)
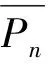
由此可见,对于任何触发次序,上述计算办法总是适用的,也就是说相控触发方式下CRT的任何调节模式均可以在多绕组调节模式下统一分析。
3 谐波分析
结合CRT工作原理可知,i1的波形符合1/4周期对称[15],其中只含基波和奇次谐波中的正弦项,可分解为如下形式的傅里叶级数
(11)
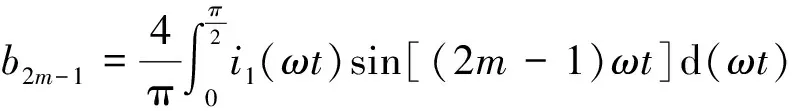
(12)
按照第2章推理,i1在[0,π/2]上是由h个分段表达式构成的,其形式由式(5)统一表示,将式(5)所示的h个分段表达式代入式(12)中进行分段积分并整理化简,便可求得工作绕组电流的2m-1(m=1,2,3,…)次谐波分量的傅里叶系数与αn之间的多元函数关系式,通过进一步化简,所得结果可表示为
(13)
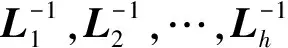
(14)
工作绕组电流基波及各次谐波分量有效值为
(15)
文献[11]提出了CRT的3种调节模式:顺次单支路(逐级短路)、固定单支路和转移单支路调节模式。就处于部分时段导通状态的绕组个数来说,这3种调节模式始终只有1个,可称之为单绕组调节模式。本文分析的多绕组调节模式包括了单绕组调节模式。事实上,对于单绕组调节模式,就是令α2=α3=…=αh-1=0,0≤αh≤π/2,αh+1=αh+2=…=αn=π/2,于是便可由式(14)和式(15)得到工作绕组电流的2m-1(m=1,2,3,…)次谐波电流(m=1时为基波)的有效值为
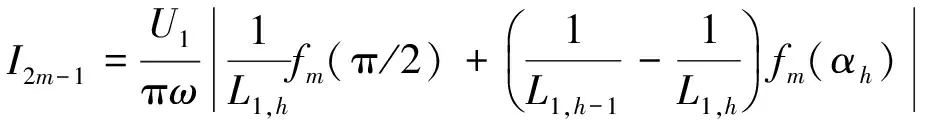
(16)
由式(16)可得工作绕组电流的2m-1次谐波电流系数(谐波含有率[11])为
(17)
特别的,在顺次单支路模式下有
(18)
式(18)中,βh就是文献[11,13]中所说的级间容量递增系数,式(18)中的第2式则将级间容量递增系数与CRT的结构参数联系在了一起,这对指导CRT设计具有重要意义。联立式(14)对式(18)进行化简发现式(18)与文献[13]中的式(13)是一致的。
虽然在形式上其余两种模式的谐波含有率也能表示成式(18),但此时,βh=L1,h-1/L1,h没有具体意义,代表的不是级间容量递增系数。
以上分析说明,本文推导的多绕组调节模式下工作绕组瞬时电流分段表达式及谐波电流的计算公式可以完全用于单绕组调节模式的分析计算,单绕组调节模式可以看作多绕组调节模式的一个特例。
按照本文的推理,对于任意结构的CRT,只要能给出其各绕组间的自、互电感及限流电感的值,根据式(6)~式(8)就可以得到任意触发角组合下CRT工作绕组电流的瞬时表达式,而根据式(13)~式(15)可以求得任意触发角组合下CRT工作绕组电流的各次谐波分量有效值。
4 算例验证
为验证本文所给计算方法与推理过程的正确性,本文以文献[11]中提供的CRT模型参数为例进行分析计算,并与文献[11]中提供的CRT等值电路仿真模型的仿真结果进行对比。
设电力牵引母线的额定电压为UN=27.5 kV,文献[11]给出了一个6绕组CRT,并求出了各绕组之间的自、互阻抗矩阵(各绕组的匝数和所有物理量均已归算到了高压侧),将阻抗矩阵转化为自、互电感矩阵(用M表示,M的每行(每列)元素对应的实际绕组编号为标准排列),结果(单位:H)如下
M=

文献[11]的算例是针对顺次单支路模式(逐级短路调节模式)来设计的,当M矩阵确定之后,采用文献[11]给出的递推算法便可算出对应于W2、W3、W4、W5、W6的限流电感系数,用向量Lx表示(单位:H),结果如下
Lx=[85.66 71.64 29.91 10.22 1.26]
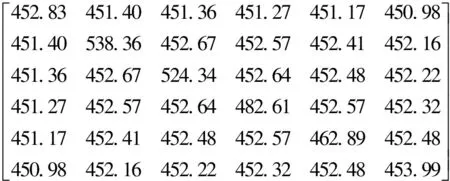
L6=

按照第2节的推理过程,可得y6为
y6=[0.00221 0.0324 0.0436 0.0524
0.109 0.226]
利用y6中的参数,根据式(6)~式(8)及工作绕组电流波形的对称性可绘出工作绕组电流在[0,π]上的波形。
文献[11]建立了CRT的等效电路仿真模型,如图3所示,其核心部分为多绕组变压器的多边形等效电路。本例中的CRT共有6个绕组,该6绕组变压器的等效电路如图3中的正6边形所示。
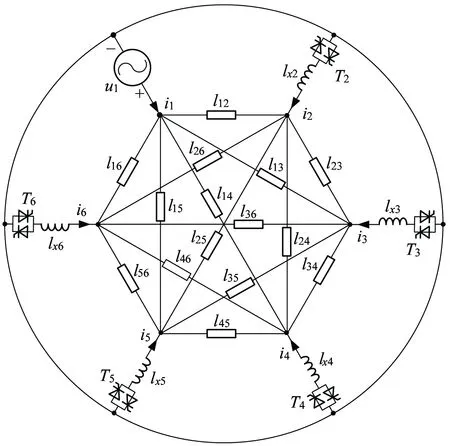
图3 CRT等效电路
按照文献[11]所给的详细计算流程,图3中的6边形等值电路各支路的等效电感参数可由CRT的自、互电感(M矩)求得,本文只列出其最终结果(用矩阵l表示),其详细过程可参考文献[11],此处不再重复。需要说明的是l的各行号与列号分别对应于等值电路的6个节点,主对角线上的元素“-”表示无效,l中各电感参数具有等效的性质,出现负值时只有数学意义,并不具有物理意义。
图3中的lij(1≤i,j≤6)是矩阵l的第i行第j列元素,lxi(2≤i≤6)为Lx的第i-1个元素,即与绕组Wi串联的限流电抗的电感大小。
将采用该仿真模型得到的波形与使用本文计算公式绘出的波形进行对比,如图4所示。
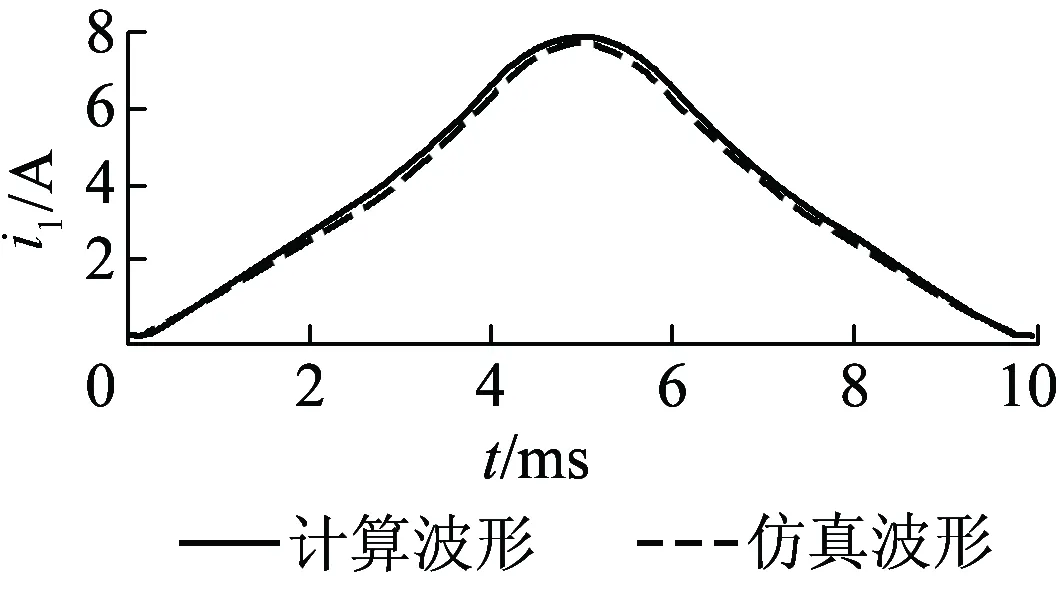
图4 工作绕组电流波形
从图4可以看出,计算所得波形与仿真波形基本重合,从而说明本文所得的计算工作绕组电流瞬时值的分段矩阵表达式是正确的。
根据式(13)~式(15),基于本例中所给的各绕组的实际触发角便可求出工作绕组电流基波与各次谐波分量有效值,见表1。
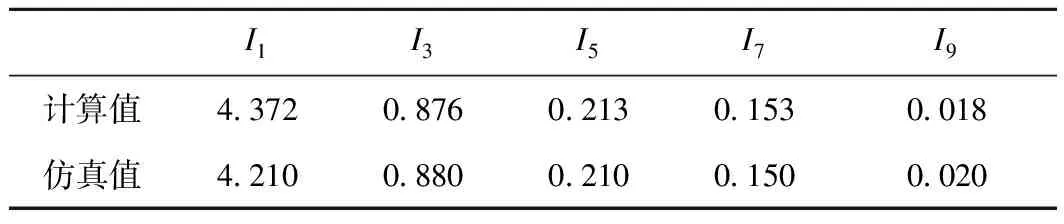
表1 基波与谐波分量有效值 A
表1显示计算结果与仿真结果基本吻合,说明本文所给出的求算工作绕组基波及各次谐波电流有效值的计算公式是正确的。
如前文所述,满足同一输出容量的触发角组合有很多组,现任意给出两组能保证相同基波电流有效值的实际触发角组合,比较其谐波含量的差异。
第一组:W2、W3、W4、W5、W6对应的触发角依次为0、0、0、0、π/32。
第二组:W2、W3、W4、W5、W6对应的触发角依次为π/2、3π/8、7π/16、2π/13、0。
图5所示为上述两组触发角组合对应的工作绕组电流在[0,π]上的波形。上述两组触发角组合对应的CRT工作绕组基波及各次谐波电流有效值见表2。
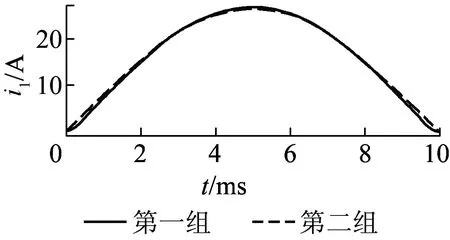
图5 两组不同触发角组合下的工作绕组电流波形
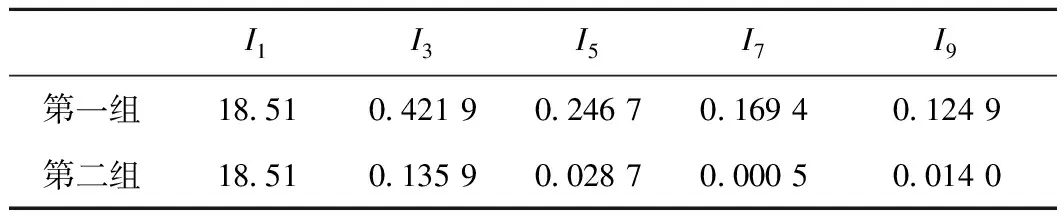
表2 两组不同触发角组合下的基波与谐波有效值 A
图5所示的两电流波形的基波电流有效值均为18.51 A。第二组组合属于多绕组调节模式,而第一组为单绕组调节模式,从表2可以看出,第二组组合对应的工作绕组电流的各次谐波明显小于第一组,这说明让CRT按照多绕组调节模式运行有可能进一步减小其谐波含量。
5 结论
(1)多绕组调节模式下,CRT工作绕组电流在各个时段上的波形可通过对相应临界波形进行平移而直接得到。
(2)多绕组调节模式下,CRT工作绕组电流各次谐波分量有效值与各个触发角之间的多元函数表达式是若干个相同形式的关于触发角的一元函数的线性组合。
(3)多绕组调节模式能够涵盖相控触发方式下CRT所有的调节模式,文献[11]中所述的单绕组调节模式是多绕组调节模式的特例,本文给出的多绕组调节模式的工作绕组瞬时电流分段表达式和谐波电流计算公式更具有一般性。
(4)本文的计算结果与采用文献[11]中的CRT等值电路模型得到的仿真结果基本吻合,说明本文的分析方法和计算公式是正确的。
参考文献:
[1]张宇,陈乔夫,李江红,等.一种用于电气化铁道无功补偿的可控电抗器[J].电工技术学报,2011,26(8):166-171.
ZHANG Yu,CHEN Qiaofu,LI Jianghong,et al.A Controllable Reactor for Reactive Power Compensation of Electrified Railways[J].Transactions of China Electrotechnical Society,2011,26(8):166-171.
[2]杨少兵,吴命利.电气化铁道牵引馈线负荷概率模型[J].铁道学报,2011,33(5):38-42.
YANG Shaobing,WU Mingli.Load Probability Model of Traction Feeder for Electrified Railway[J].Journal of the China Railway Society,2011,33(5):38-42.
[3]周福林,李群湛,邱大强.基于混合补偿的同相牵引供电系统[J].铁道学报,2012,34(1):19-23.
ZHOU Fulin,LI Qunzhan,QIU Daqiang.Co-phased Traction Power Supply System Based on Hybrid Compensation[J].Journal of the China Railway Society,2012,34(1):19-23.
[4]张丽,李群湛,贺建闽.无功反送正计条件下最佳固定补偿容量的选择[J].铁道学报,2003,25(2):34-38.
ZHANG Li,LI Qunzhan,HE Jianmin.On the Fixed Compensation Capacity Optimize under the Reactive Power Absolute Measurement[J].Journal of the China Railway Society,2003,25(2):34-38.
[5]刘弢,郭知彼,蒋家久.牵引变电所静止无功补偿方案综述[J].机车电传动,2005(6):12-14.
LIU Tao,GUO Zhibi,JIANG Jiajiu.Survey on Scheme of Static Var Compensation of Traction Substation[J].Electric Drive for Locomotives,2005(6):12-14.
[6]王卫安,桂卫华,张定华,等.基于大容量SVC的SCOTT变压器电能质量治理方案及应用[J].铁道学报,2011,33(1):31-38.
WANG Weian,GUI Weihua,ZHANG Dinghua,et al.SCOTT Transformer Power Quality Compensation Scheme and Its Application Based on High-capacity SVC[J].Journal of the China Railway Society,2011,33(1):31-38.
[7]赵伟,罗安,唐杰,等.静止无功发生器与晶闸管投切电容器协同运行混合无功补偿系统[J].中国电机工程学报,2009,29(19):92-98.
ZHAO Wei,LUO An,TANG Jie,et al.Hybrid Var Compensator Based on the Coordinated Operation of STATCOM and TSC[J].Proceedings of the CSEE,2009,29(19):92-98.
[8]王宁之.电气化铁路动态无功补偿(SVC)方案探讨及可控电抗器的应用[J].电力电容器与无功补偿,2009,30(4):5-7.
WANG Ningzhi.Investigation of Dynamic Static Var Compensation(SVC) Program for Electrified Railway and Application of Controllable Reactor[J].Power Capacitor & Reactive Power Compensation,2009,30(4):5-7.
[9]金立军,廖黎明,安世超,等.牵引供电系统无功补偿与谐波抑制[J].同济大学学报:自然科学版,2009,37(5):664-668.
JIN Lijun,LIAO Liming,AN Shichao,et al.Reactive Power Compensation and Harmonics Restraint in Traction Power Systems[J].Journal of Tongji Universty :Natural Science,2009,37(5):664-668.
[10]吴利仁,郭欲平,易运军,等.磁阀式可控电抗器在电气化铁道中的应用[J].变压器,2006,43(3):13-16.
WU Liren,GUO Yuping,YI Yunjun,et al.Applicaton of Magnetic Valve Type Controlled Reactor to Electric Railroad[J].Transformer,2006,43(3):13-16.
[11]田铭兴.变压器式可控电抗器的基本理论研究[D].西安:西安交通大学,2005.
[12]TIAN M X,LI Q F,LI Q F.A Controllable Reactor of Transformer Type[J].IEEE Transactions on Power Delivery,2004,19(4):1 718-1 726.
[13]田铭兴,励庆孚.变压器式可控电抗器的谐波分析和功率级数计算[J].中国电机工程学报,2003,23(8):168-171.
TIAN Mingxing,LI Qingfu.Harmonic Current and Power-step Number of Controllable Shunting Reactors of Transformer Type[J].Proceedings of the CSEE, 2003,23(8):168-171.
[14]周腊吾.新型特高压可控电抗器的理论及应用[D].长沙:湖南大学,2008.
[15]王兆安.谐波抑制和无功功率补偿[M].北京:机械工业出版社,2005:12-21.

