结合相角重构法的轨道不平顺随机过程的数值模拟
徐 宁, 任尊松, 李 响
(北京交通大学 机械与电子控制工程学院, 北京 100044)
车辆运用过程中,由于轨道和车辆不断地相互作用,会使轨面逐渐产生不均匀磨耗, 轮对踏面出现擦伤、不圆等不良损坏,这些破坏又极易形成反作用于车辆-轨道系统的扁疤、表面不圆和波纹形激励。与此同时,由于钢轨扣件、轨枕、道床和路基等部件弹性不均,各部件之间存在间隙以及长时间使用的破坏损耗使轨道系统的几何状态逐渐发生改变,产生轨道不平顺。研究发现轨道不平顺是一个随机过程[1], 是引起车辆-轨道系统随机振动的主要外界激励,直接关系到行车安全和车辆运行的舒适性。
为便于在车辆动态模拟与仿真以及进行轨道系统病害诊断等领域应用,德国、美国等通过对轨道不平顺进行实测和分析,构造了形式较为统一的谱密度函数[2]。中国铁道科学研究院以及长沙铁道学院等研究单位也曾对国内一些个别线路的轨道不平顺进行了测量和研究,相应地建立起一定标准的谱密度函数的表达式[3]。这些研究得到的谱密度函数均在频域范围内给出,但在车辆运行稳定性、平稳性和安全性分析等方面都直接需要轨道不平顺的时间-历程作为输入激励。因此,通过数值模拟获得轨道谱的时域序列,是车辆和轨道动力学研究中不可回避的问题。很多研究人员也对此开展了研究工作,总结了轨道不平顺数值模拟的几种主要方法,包括白噪声滤波法[6]、三角级数法[5]、二次滤波法[4]、小波变换法[7]和逆傅里叶变换法[8]。这些方法较为常用,但同时也存在一定的不足,二次滤波法需依据轨道不平顺谱密度函数的不同,设计出合理的滤波器;小波变换法获得随机时域序列与小波基的选取有关;白噪声滤波法以及三角级数法需将模拟的不平顺随机序列看作是平稳高斯过程。且通过这几种方法获得时域序列经FFT的变换谱与原轨道谱存在一定的差距。逆傅里叶变换法[8]计算速度快,且模拟得到的时域序列经FFT的变换谱与原不平顺谱较为一致。但该方法得到的时域随机序列的正态性与否不确定,样本数字特征也不确定,这与文献[9-10]中实测得到的线路不平顺为具有一定偏度和峭度范围的非正态随机过程并不能完全相符。与此同时,当车辆在处于匀速状态下,不平顺激励在时间域还是在空间域都是平稳过程。但变速条件下运行时,不平顺在时间域上已是非平稳的随机过程[14],作为激励输入到车辆和轨道系统之中,获得的各部件响应也较匀速条件下有所差别。为在不同运行工况下,获得更为准确的车辆系统响应特征,进而分析系统频域传递等特征,获取变速条件下的不平顺随机序列十分必要。
鉴于此,本文在逆傅里叶变换方法基础之上,依据实测线路不平顺峭度和峰度等数字特征的变化范围,采用相角重构方法获取了具有一定峭度值和峰度值的平稳随机序列。由于变速过程中轨道不平顺谱为慢变的时变功率谱,将变速过程看作多个短时段内的匀速过程,使时变功率谱转化为各时段上的平稳功率谱,并通过逆傅里叶变换法分别得到各时段对应的随机时域序列,利用相角重构方法实现各序列的连接,得到加速和变加速过程的非平稳轨道不平顺时域序列。
1 具有一定偏度值和峭度值的随机时域序列获取
1.1 由逆傅里叶变换法生成随机时域序列
根据逆傅里叶变换方法[8]进行轨道谱的数值模拟,其实现步骤如下:
Step1首先将不平顺单边功率谱密度函数转化为双边谱密度函数。进而将得到的空间双边不平顺功率谱S(Ω)转化为时间功率谱S(f)。设车辆运行的速度为v,轨道不平顺的最大波长为λmax,最小波长为λmin,则模拟的频率范围最大值为fmax=v/λmin,最小值为fmin=v/λmax。根据采样定理,时域采样间隔应满足Δt≤0.5fmax。假定总的模拟时间为T,那么时域采样点数为T/Δt,一般需保证其个数Nr为2的整数次幂,频率采样间隔为Δf=1/(NrΔt),有效频段内采样点数为Nf=(fmax-fmin)/Δf,由周期图法估计出的功率谱为偶对称序列,在Nr/2-Nf~Nr/2+Nf频率区间内的采样点记为零,得到在1~Nr/2上功率谱的Nf个离散采样点值S(f=kΔf),k=0,1,…,Nr/2及在Nr/2+1~Nr-1上离散采样点值S(f=kΔf),k=Nr/2+1,…,Nr。
Step2根据周期图法,可获得各频率采样点的频谱模值为
X(k)=DFT[x(n)]=
( 1 )
Step3所求时域序列x(n)为一随机过程,要求其FFT得到的复序列X(k)的相位需具有随机性。设ψn是均值为零的独立相位序列,那么ψn应为复数,且满足|ψn|=1,即
ψn=cosβn+i sinβn=exp(iβn)
( 2 )
式中:βn为在[0,2π]上服从均匀分布的随机相角。且X(k)的虚部关于Nr/2奇对称,实部关于Nr/2偶对称,因此只需求出k在0~Nr/2间各频率采样点处的频谱值X(k),其表达式为
( 3 )
Step4将式( 3 )中得到的序列X(k)进行傅里叶逆变换,可获得相应的不平顺时域序列。
( 4 )
1.2 通过重构相角生成具有一定统计特性的随机时域序列
对均值为零的随机时域序列,根据偏度和峭度的定义,其表达式为
( 5 )
( 6 )
对于随机位移-时间历程x(t),其各阶原点矩均可以通过积分逼近,即
( 7 )
将式( 7 )代入到式( 5 )和式( 6 )之中,按照文献[11]方法,经过化简,序列的偏度和峭度可表达为关于功率谱幅值和随机相角的形式
( 8 )
( 9 )
式中:Ak、Aj、Am、An为功率谱中各频率点的幅值;φk、φj、φm、φn是[0,2π]上均匀分布的随机相角,经证明[11],为不影响对功率谱的精确模拟,可使得式( 8 )和式( 9 )中Ak和Aj等各幅值不变,通过调整随机相位角中一部分进而改变生成随机时域序列的峭度和偏度值,也使得相位角的整体随机性得以保证,进而确保重构相角后得到的时域序列仍为随机序列。
例如对式( 8 ),取下标为j=2k的各组相位角φk和φj(如{φ1,φ2},{φ2,φ4},…)符合关系φj=2φk,那么cos(φj-2φk)的值恒为1,偏度值S逐渐增大;或符合关系φj=2φk+π,使cos(φj-2φk)的值恒为-1,偏度值S逐渐减小。
1.3 改进相角重构方式获取随机不平顺序列
逆傅里叶变换方法应用过程中,生成的随机相角是伪随机数,以至于得到的随机序列虽然均值接近于零,但往往并不是高斯序列,峰度值和峭度值大小也不确定。且轨道谱本身为频变谱甚至为折线谱,而非文献[11]中所采用的平直功率谱,所以仅采用文献中绝对正向和绝对反向这样两种相角重构方式重构相角,往往会造成找寻效果比较差;甚至某些情形下,无法获得目标参数下的随机时域序列,鉴于此,以文献[11]中方法为基础,并改进原有方法,可获得兼具目标偏度值S*和峭度值K*的随机序列,具体实现过程步骤:
Step1根据偏度S和峭度K表达式中第一个三角函数项,在已有的Nr/2个[0,2π]上均匀分布的随机相位角中找出所有下标满足关系j=2k和m=3n(0≤j,k,m,n≤Nr/2-1)的各组相角组合{φj,φk}和{φm,φn}。数据长度较大时,满足上述条件的相角很多,其集合可记作{φj1,φk1;φj2,φk2;…}和{φm1,φn1;φm2,φn2;…}。

Step3继续按照Step2中的方式,选取后续的多对相角。例如第x次重构的两组相角分别为{φjx,φkx}和{φmx,φnx},为减小重构过程中偏度和峭度间的相互影响,当φjx为6的公倍数的情形,跳过该组相角,选取下一组对应相角{φj(x+1),φk(x+1)}。再次计算新生成序列的偏度和峭度值Sxil和Kxil,并按照步骤Step2中的方式进行检验,如e(Sxil)和e(Kxil)处于规定的范围之内,停止重构,获得满足要求的随机序列。如果仍超出规定的范围,可按照Step2中的方式,确定该次重构的最优方式。并对后一组相角进行类似的重构,直到e(Sxil)和e(Kxil)小于规定限值ξS和ξK为止。
2 变速过程的非平稳随机时域序列的获取
匀速运行时,轨道不平顺激励可视为平稳的随机过程。当车辆处于加速启动和减速制动等运行工况下,轨道不平顺在空间域上是平稳的,但在时域上是非平稳的随机过程。此时,不平顺谱转变为慢变的时变功率谱。首先,将模拟序列总的时长拆分为多个较短的时间段,在这些较短的时间段上,时变功率谱可近似看做非时变,可求得各时间段上的功率谱密度函数表达式,通过逆傅里叶变换方法可获得各时段的随机序列。基于此,利用相角重构的方法将各段随机序列首尾相连接,即可获得变速过程的非平稳随机时域序列,其具体实现过程如下。
2.1 轨道谱转化为各短时间段上平稳功率谱
根据时域和空间域的转化关系式
ft=Ωs
(10)
式中:Ω为空间频率;s为走行距离。瞬时频率表达式为
fs=Ωds/dt
(11)
车辆在匀加速情况下
(12)
车辆在变加速度情况下
(13)
式中:v0、a0分别为速度和加速度的初始值;a、u分别为加速度和加速度的变化率。
可得到轨道不平顺在匀加速和变加速工况下的时变功率谱,即
(14)
(15)
子段划分数M的选取,应使得各子段任意频率点对应的时变功率谱S(f,t)满足式(16),且M的取值一般为2的整数次幂。
(16)
式中:fj为功率谱频域范围内任一频率点;timin和timax为第i个子时间段的上、下时刻点;δ为一很小的正数。
设模拟的总时间为T,已划分时间段数为M,那么各子段的时长Ts0可暂定为T/M,根据时域采样间隔为Δt,子段时域采样点数为Ts0/Δt,若满足2j-1 根据得到各子段时长Ts,计算出各子段中心时刻Ti mid(i=1~M),依据式(14)和式(15),将时变功率谱S(f,t)转化为各子段的中值时刻功率谱S(f,timid)。基于得到的各中值时刻功率谱S(f,timid),并利用1.1中逆傅里叶变换法,即可获得各子段的随机时域序列。 通过2.1节的过程得到了各子段的随机时域序列,但这些序列在每一段的末尾时刻以及下一段的初始时刻的函数值并不连续,显然与真实情况不相符。参照相角重构的方法,实现各子段随机序列的连接按照以下具体步骤: Step2利用逆傅里叶变换法重新生成随机序列,经过第j个相角重构后,获得的该子段序列的初始时刻位移值x(i_j)start_k,按式(17)计算出各x(i_j)start_k与x(i-1)last的绝对误差。 δi_j_k=|xi_jstart_k-x(i-1)last| (17) 式中:i为当前子段数;j为该段第j个重构相角;k为该相角第k个重构方向。 Step3将已得到的各δi_j_k与规定限值ξ进行比较,若某一δi_j_k小于规定限值,那么对应的时域序列即为所求,如果k=0~2r的任一重构方式均不能小于规定限制ξ,那么比较各δi_j_k(k=0~2r),求出其中最小值min(δi_j_k),并将其对应重构方式作为本次重构的最优方式。选取下一重构相角φj+1,按照Step1的方法进行重构,直到得到δi_j_k小于规定限值ξ为止。 Step4以步骤Step3得到序列的末尾时刻位移值xilast为基准,多次重复Step1~ Step3,实现后续多段随机序列的连接,直到最后一段为止。 为验证本文方法的有效性和实用性,结合两个不同算例,利用重构相角方法对高速铁路无砟轨道谱进行时域转化。 根据文献[9]的建议,模拟的轨道长度为1 024 m,而文献[10]中通过正线实测高低不平顺数据并进行统计分析,得到不平顺序列的偏度值范围为-1~1之间,峰度值位于零值附近。为不失一般性,本文选取生成随机序列的目标峭度为0,目标偏度取值分别为0、-0.5和0.5,模拟的运行速度为v为80 m/s(288 km/h),时域采样间隔Δt为10-4,轨道不平顺波长范围为3~100 m,规定限值ξS和ξK分别为0.01和0.02。 取高速无砟轨道高低不平顺谱为转化对象,其表达式为分段幂函数,具体可见式(18),各分段对应的相关参数见表1。 SΩ=A/Ωk (18) 式中:Ω为空间频率;A、k为拟合公式系数,1/m。 表1 无砟轨道不平顺中位谱拟合公式系数 1/m 高速铁路无砟轨道谱为分段线性谱,各段间分段点对应空间波长和频率可见表2。 表2 高速铁路无砟轨道不平顺谱分段点空间频率及对应波长 图1、图2分别为逆傅里叶变换法得到的随机序列以及不同目标峭度和目标偏度下的随机时域序列。 从图1、图2可以看出,经过本文方法调整得到的具有一定偏度和峭度值的随机序列在数值范围上与逆傅里叶变换法直接获得的随机序列相近,说明了该方法的可用性。不同偏度和峭度值对应的时域序列的整体走势有很大的不同,说明了偏度和峭度对于随机序列确实有一定的影响。 表3为各随机序列的均值、方差的统计特性。表中显示重构相角后得到的新随机序列的均值和方差与原序列几乎没有差别,并能保证序列的偏度和峭度较高的精度地接近目标值。随着偏度值从-0.5~0,再由0逐渐增大到0.5,各随机序列的中位数也对应地出现了逐渐增大的过程,偏度为0.5序列与偏度为-0.5序列的中位数相差达到1.25,峭度值由基本序列的-0.103左右到达0附近,数值处于均值±2周围的点的个数多了近8 000。统计特征的对比结果说明偏度和峭度对随机序列整体特点确有一定的影响。 表3 匀速条件下各序列统计特征及其对比 由图3可知,重构相角后得到的新随机序列及逆傅里叶变换法得到初始序列,经FFT的幅频谱与转化谱都非常接近,说明本文方法的模拟结果精确性。 仍以算例1中的高速铁路高低不平顺为转化对象,模拟的轨道长度约为2 048 m,以v0=77 m/s(277 km/h)作为车辆在加速过程中的初始速度,将之后的加速过程分别看做是加速度为a=0.2 m/s2的匀加速运动与加速度为a=0.2 m/s2、加速度变化率为u=0.01 m/s3变加速运动两种情形,并假设二者各子段的初始随机相位角相同,获得匀加速过程和变加速过程对应的不平顺位移-时间序列见图4。 由图4可以看出,匀加速过程和变加速过程随机不平顺序列整体趋势和数值范围上比较一致,但各局部极值的大小及最大值和最小值出现的位置均存在差异,且随着时间的增长,二者在局部上差异更为明显,说明加速度变化率的对随机序列的走势有一定影响。 表4给出匀加速和变加速过程下两随机序列的统计特征及其平稳性检验结果。 表4 随机序列的统计特征及平稳性检验结果 由表4见,重构相角方式获得的匀加速和变加速过程的轨道随机序列是非平稳的,而系统的均值仍然在零值附近,方差与匀速过程轨道随机序列相近。 由图5可以看出,由重构相角方法获得的匀加速过程和变加速过程的随机序列,经FFT变换得到的功率谱,二者数值上略有差别,且都与原不平顺功率谱较为接近,说明本文方法获得的模拟序列的可用性和准确性。 (1) 本文通过二次重构随机相角的方法可以比较准确的将由逆傅里叶变换法得到的不平顺随机序列转化具有一定偏度和峭度值的随机序列,能够保证序列的均值和方差等统计特征不发生较大改变。偏度和峭度对时域序列的整体走势,中位值以及均值附近±2周围的样点的个数均有不小的影响。 (2) 将加速过程和变加速过程下时变功率谱转化为一些较短时间段上平稳功率谱,利用逆傅里叶变换法获得各时间段的随机时域序列,通过重构相角方法实现各段序列的连接,最终获得了变速过程下的轨道随机不平顺序列。发现变速过程下不平顺序列具有非平稳的特点,其均值和方差等统计特性与匀速过程下较为接近。且变速过程的随机不平顺序列经FFT变换得到的功率谱与原不平顺功率谱数值上较为一致。匀加速过程和变加速过程下随机不平顺序列的整体趋势和数值范围上比较一致,但各局部极值的大小及最大值和最小值出现的位置均存在差异,且随着时间的增长,局部上差异越明显。 参考文献: [1] 罗林.轨道随机干扰函数[J]. 中国铁道科学,1982,3(1):74-112. LUO Lin. Track Random Irregularities Function[J]. China Railway Science,1982,3(1):74-112. [2] 翟婉明.车辆-轨道耦合动力学[M].2版.北京:中国铁道出版社,2002. [3] 长沙铁道学院随机振动研究室.关于机车车辆-轨道系统随机激励函数的研究[J].长沙铁道学院学报,1985,1(2):1-36. Research Group on Random Vibration of Changsha Railway Institute. Research on Random Excitation Function for Rolling Stock/Track System[J]. Journal of Changsha Railway University,1985,1(2):1-36. [4] 王元丰,王颖,王东军.铁路轨道不平顺模拟的一种新方法[J].铁道学报,1997,19(6):110-115. WANG Yuanfen, WANG Ying, WANG Dongjun. A New Simulating Method for the Irregularities of Railway Tracks[J]. Journal of the China Railway Society,1997,19(6):110-115. [5] 星谷胜,常保琦.随机振动分析[M].北京:地质出版社,1977:42-62. [6] 钱雪军.轨道不平顺的时域模拟法[J].铁道学报,2000,22(4):94-98. QIAN Xuejun. Track Irregularity Simulation in Time Domain[J]. Journal of the China Railway Society,2000,22(4):94-98. [7] 何越磊,陈施宇,李再帏.基于小波变换的轨道不平顺数值模拟方法[J].城市轨道交通研究, 2014,17(10):59-62. HE Yuelei, CHEN Shiyu, LI Zaiwei. Track Irregularity Simulation Based on Wavelet Transform[J]. Urban Mass Transit,2014,17(10):59-62. [8] 陈果,翟婉明. 铁路轨道不平顺随机过程的数值模拟[J].西南交通大学学报,1999,34(2): 138-142. CHEN Guo, ZHAI Wanming. Numerical Simulation of the Stochastic Process of Railway Track Irregularities[J]. Journal of Southwest Jiaotong University,1999,34(2):138-142. [9] 康熊,刘秀波,李红艳,等.高速铁路无砟轨道不平顺谱[J].中国科学:技术科学,2014,44(7):687 -696. KANG Xiong, LIU Xiubo, LI Hongyan, et al. PSD of Ballastless Track Irregularity of High Speed Railway[J]. Scientia Sinica:Technologica,2014,44(7):687-696. [10] 中国铁道科学研究院基础设施检测研究所.2013年JC字第157号 高速线路不平顺谱的研究[R]. 北京:中国铁道科学研究院基础设施检测研究所,2013. [11] 蒋瑜.频谱可控的超高斯随机振动环境模拟技术及其应用研究[D].长沙:国防科学技术大学,2005. [12] 蒋瑜,陶俊勇,王得志,等.一种新的非高斯随机振动数值模拟方法[J].振动与冲击, 2012, 31(19):169-173. JIANG Yu, TAO Junyong, WANG Dezhi,et al. A Noval Approach for Numerial Simulation Method of a Non-Gauss Random Vibration[J]. Journal of Vibration and Shock,2012,31 (19):169-173. [13] 李茂清,王洁,陈强,等. 基于MATLAB程序的FIR滤波器设计实现[J].电力学报,2008,23(2): 87-90. LI Maoqing, WANG Jie, CHEN Qiang, et al. The Accomplishment of the Design of FIR Filter Design Based on MATLAB Program[J]. Journal of Electric Power,2008,23(2):87-90. [14] 张立军.车辆非平稳行驶动力学及控制研究[D].沈阳:东北大学,2006.2.2 基于相角重构实现各段随机序列连接

3 数值算例及结果分析
3.1 算例1
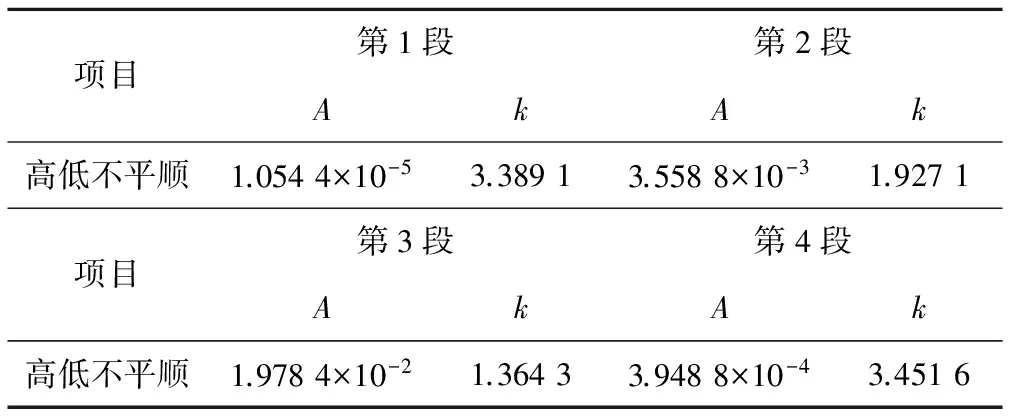

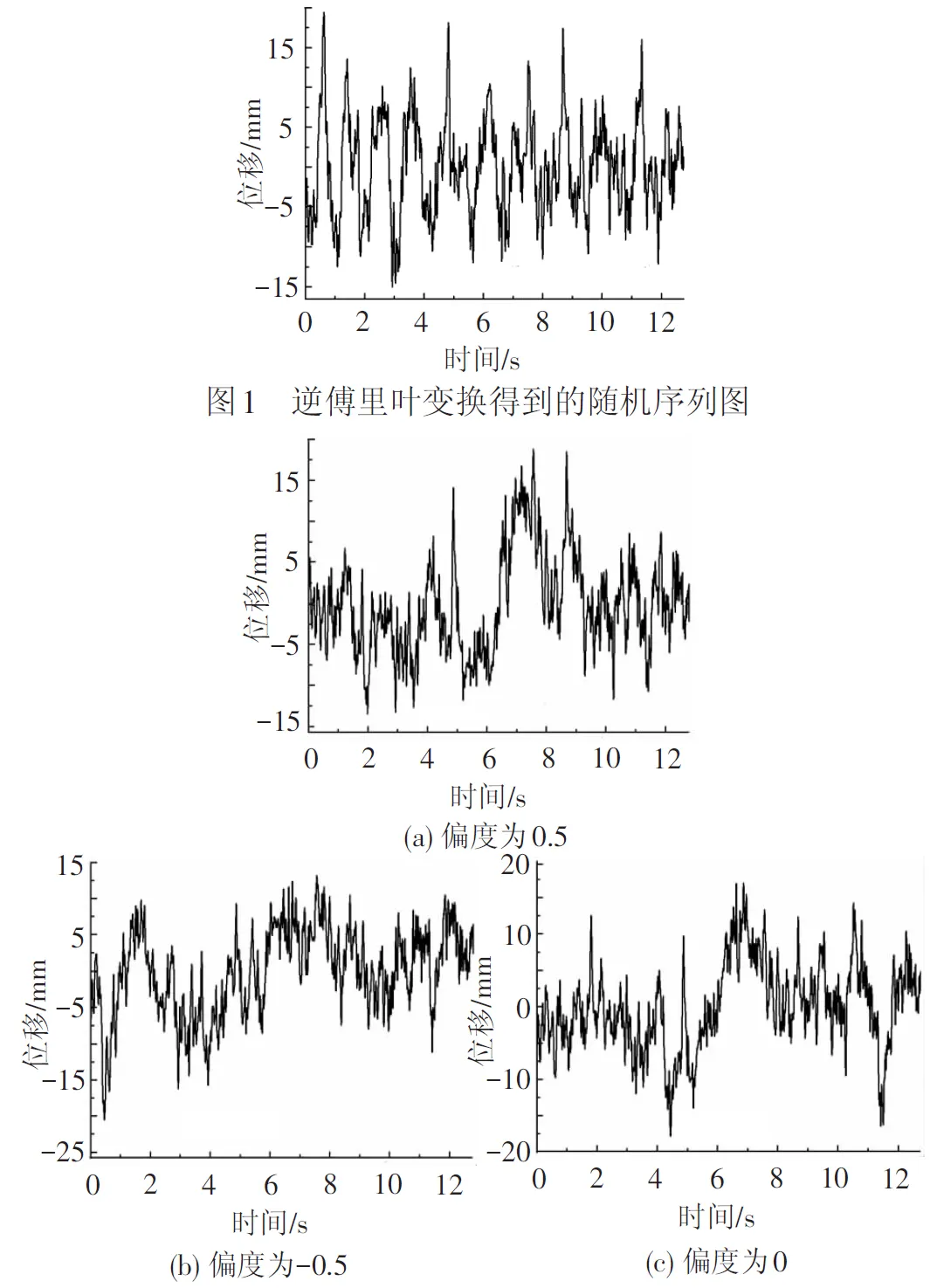


3.2 算例2



4 结论

