基于离散小波变换的接触网横向风振响应研究

韩南南， 杨 俭， 袁天辰， 宋瑞刚

(上海工程技术大学 城市轨道交通学院， 上海 201620)

接触网的稳定性直接决定弓网受流的质量，影响列车的运行安全。接触网受到横向风作用时偏离初始位置，并产生振动。持续的风振降低接触网的疲劳强度及列车运行可靠性，当风偏较大时不仅增加钻弓的概率，严重时可使结构产生弯曲甚至失稳现象，使弓网受流不稳定[1-2]，因此，对接触网横向风致振动研究尤为重要。风场具有非平稳信号的特性，一般将随机风场分为脉动风与平均风两部分，脉动风具有随机动力性质[3-7]，而平均风在同一地域同一时间段具有静态特性。由于横风载荷对接触线结构作用复杂，精确计算接触网横向振动困难，目前多采用有限元方法。文献[4-5]研究了随机风场下接触网风振响应对受流质量的影响，但未考虑最大风载对接触网横向偏移的影响，而最大风载是决定接触网横向偏移大小的主要因素。文献[6]基于AR模型模拟了随机风场，研究了接触网的模态、静态风偏和风振响应，但是其预测效果受模型选择、阶数等因素的影响很不稳定。文献[7]利用正交小波逆变换模拟出风速时程，结果证明功率谱函数和互相关函数与目标值符合较好。

本文应用离散小波分析数值模拟水平方向脉动风速时程；通过分析线索结构的动力学特性，建立接触线振动微分方程；将随机风场，平均风速及最大风速模型施加到接触网模型中。利用数值方法，分析接触网沿跨距不同位置的振动响应，对最大风速作用下的风偏进行仿真，研究接触网不同跨距、不同风速及不同风向角对接触网横向偏移的影响。

1 接触网随机风场模拟

在工程结构应用中，作用在接触网上的顺向风由平均风与脉动风共同作用[7]，平均风载是根据实测结果周期在10 min以上的长周期部分，远大于接触网自振周期，其作用效果按静力学分析[4]；脉动风载是自振周期在几秒钟至几十秒以内的短周期部分，其与接触网自振周期较接近，其作用效果具有动态特性[7]。

1.1 静风场[1]

m个点的风速时程向量V(t)=[V1(t)V2(t)V3(t) …Vm(t)]T可表示为[8]

( 1 )

平均风速向量采用指数变化规律，即

( 2 )

1.2 脉动风场

脉动风速采用广泛使用的Davenport功率谱，见图1。

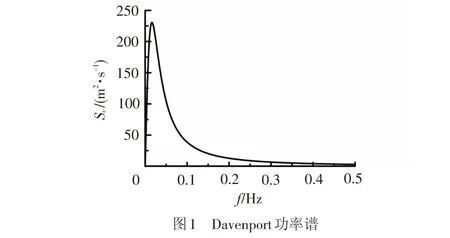
其数学表达式[4]为

( 3 )

式中：Sv(f)为脉动风速功率谱；f为脉动风频率；v10为10 m高度处的平均风速；k为地面粗糙度系数。

对于空间上不同的2个点i、j，其相关性可通过空间相干函数描述[7]，则2个点的互谱密度函数Sij(f)可由自谱密度Sii(f)、Sjj(f)与相干函数rij(f)确定[8]，即

( 4 )

脉动风速的三维空间相干函数为

rij(f)=exp

( 5 )

1.3 风场的数值反演

风场时域模型，较多使用谐波叠加法和线性滤波器法，但这些方法存在精度与效率的矛盾。本文采用小波分析法，其具有多分辨率的特性，每重构一次，样本数据就扩展约一倍，同时其频率范围也向高频扩展一倍。这样分解层数达到一定值，模拟样本能含有必要的高频信息，从而使其所产生的单点脉动风速时程样本的统计参数与目标很好地吻合。

白噪声是一种功率谱密度为常数的随机信号或随机过程。因为白噪声信号在各个频段上的功率一样，对其处理可以得到符合一定功率谱密度特性的信号。所以本文选择高斯白噪声作为构造脉动风信号的源信号。小波分析模型是将高斯白噪声经过小波分解、小波系数比例收缩和小波重构，得到符合谱密度特性的风速时间序列[9-10]。

给出长度为N的高斯白噪声时间序列XN,对其进行小波分解得到如下小波系数

X0,d0,d1,…,dJ-1

( 6 )

式中：X0是低频部分的小波系数；di是高频段的小波系数；J是小波分解的层数。本文所取白噪声长度N为2 048，对其进行10层分解。

依据多分辨分析的基本思想，总数为2M个点的风速时程采样数据可近似认为与最精确尺度上的剩余系数相等。下一尺度上小波系数的个数为2M-1，当采样频率为f时，该尺度对应的频段区间为(f/2,f)；再下一尺度上小波系数的个数为2M-2，该尺度对应的频段为(f/4,f/2)。以此类推，在最粗糙尺度上，小波系数的个数为1，其对应的频段为(f/2M,f/2M-1)，在该尺度上剩余系数的个数为1，对应频段区间为(0,f/2M)。

小波系数收缩是对每一频段小波系数都乘以一个相应的比例值li，即

X0,l0d0,l1d1,…,lN-1dN-1

( 7 )

式中:li即为小波收缩系数，如下

( 8 )

对高斯白噪声高频段的小波系数作如下处理

( 9 )

(10)

进而进行小波重构，得出风速时程曲线。

本文针对简单悬挂接触网，取一个跨距为研究对象。分别对接触线和承力索施加风载，模拟水平方向脉动风速时程，风场模拟参数见表1[8]。

表1 风速时程模拟时的主要参数

根据施工条件，接触线悬挂高度为6.45 m，承力索悬挂点高度为8.05 m，分别模拟安装点处风速时程,见图2。

1.4 接触网所受风负载计算

本文研究中，风偏设计风速采用空旷地区、距地面10 m高度处自动记录50年一遇的10 min平均风速最大值。主要研究线索受最大风载，即风向与线索垂直时的风偏，线索单位长度的风负载公式由下式决定[11]

P=0.625gkdlv2sinθ

(11)

式中：g为风速不均匀系数，见表2；k为风载体形系数，见表3；d为线索直径；l为接触悬挂跨距；v为风速；θ为风向与接触线的角度。

表2 风速不均匀系数

表3 风负载体型系数

2 接触网模型建立

接触网系统受多种因素影响，振动复杂，要完全反映接触网真实振动特性非常困难,因此这里我们作一些近似的假设：

(1) 接触网受风负载沿跨距均匀分布；

(2) 承力索、接触网视为具有均匀密度与抗弯特性，吊弦线性质量远小于承力索，忽略吊弦质量，等效为弹簧单元;定位器、支撑杆不考虑横向振动，等效为弹簧单元;

(3) 考虑接触网的抗弯性、抗压性，其承力索与接触线采用欧拉伯努利梁模型。

2.1 接触网物理模型建立

接触网系统包括承力索、接触线、支撑装置与定位器等结构，图3为简单链形悬挂一个锚段的接触网模型[12-15]。

图3中:TA、TB分别是承力索与接触线的张力；P为风载；Kci为第i个腕臂与承力索之间的弹性刚度；Kpi为第i个支撑杆与接触线之间的刚度；Kdi为第i个吊弦的刚度；Mdi为第i个吊弦的质量；EIA、EIB分别为承力索与接触线的抗弯刚度；ρA、ρB分别为承力索与接触线的线密度。接触网参数见表4[16]。

表4 接触网参数

接触网受到风载作用时产生横向振动及偏移，偏移大小决定于风速的大小、方向以及接触网的结构，由于列车通过一个跨距的时间很短，可以假设在列车通过一个跨距时间内，风速恒定，这里研究风速取最大值时的横向偏移，所以取风速与接触线垂直的方向。由于线路之字形布置，一个跨距内接触网系统风载荷下的静态示意图见图4。其中AB，BC，CD为无外载荷下接触网状态，弧线AEB为接触网受到风载后的偏移，ab为弓头滑板，列车速度为v，风载为P。

2.2 接触网受风偏移计算

研究简单链形悬挂的受风偏移状态，考虑补偿器的补偿作用，接触网在受风状态下导线张力不变，在直线区段，考虑接触网的之字布置，拉出值分别为bA和bB，距原点x的点H拉出值记为es，相应风偏值为ew，风向与接触网垂直，见图5。直线AB为无风下接触线的自由状态，A、B为接触线定位器，曲线ACB为风载作用下接触线风偏[11]。

既有坐标系下H点拉出值es可表示为

(12)

假设接触网为等之字值布置，接触线在横向负载作用下沿跨距任意点对线路中心的偏移值ew为

(13)

统一拉出值和风偏值的矢量方向，得到H点的横向位移值为

ex=es+ew

(14)

式中：b为接触线之字值，mm；P为接触线单位长度上的风负载，kN/m;T为接触线张力，kN；L为跨距长度，m。

2.3 接触网受风振动微分方程

承力索与接触线均为线索结构，将其等效为具有一定刚度的欧拉-伯努利梁，刚度沿跨距均匀，这里任取一个微分段dx进行分析[12-14]。根据振动理论[17]，通常重力与吊弦的静变形抵消。接触线振动系统，只要取静平衡位置为坐标原点，其受力图见图6。

图6中，y(x,t)为横向风力所产生的位移；ρ为单位长度的质量；EI为该微分段的抗弯强度；Q、M、T分别为截面的剪力、弯矩和轴向拉力；f0为悬挂自身所具有的阻尼。在水平方向根据牛顿第二定律可得[18-19]

Q-Q+dQ+Pdx-f0dx=

(15)

对微单元右侧面中心求力矩，由∑M=0得

(16)

即求得具有一定刚度的接触线微分段振动微分方程

(17)

式中：φ(0,t)=0,y(L,t)=0,y(0,t)=0,φ(L,t)=0。

求解四阶偏微分方程，将接触线的横向位移近似表示为

(18)

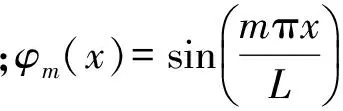
(19)

式(19)即为接触线振型坐标二阶常微分方程组的基本形式。

综上，不同风载下的接触网不同风偏对应关系见表5。

表5 风载类型及风偏对照关系

3 接触网数值模拟分析

3.1 直线区段风偏分析

通过以上分析，研究直线区段接触网风载作用下的振动特性，其中接触网跨距为65 m，根据式(14)、式(18)，令bA=bB=300，即当之字值相等时，接触线与承力索沿跨距位置10、22、33、45、58 m处，随机风载作用下的振动偏移见图7，随机风载与平均风载对接触网平均偏移的对比见图8。

仿真结果表明：

(1) 从图7可以看出，接触网在随机风载作用下发生横向振动，脉动风是引起接触网振动的主要原因，接触网跨中振幅较大，沿跨距靠近悬挂点处振幅减弱，由此可得定位器的刚性对接触网横向振动具有一定的制约。脉动风所引起的接触网长期振动在一定程度上会降低接触网的疲劳强度。

(2) 从图8仿真结果可知，平均风载是引起接触网横向偏移的主要因素，平均风载只能反映风场风速的均值，最大风载引起的接触网横向偏移是造成接触网事故的主要原因。

(3) 从图9仿真结果可知，平均风载下接触线跨中点位偏为86.3 mm，将最大风载、平均风载作用于接触线，由于理论接触线横向偏移没有考虑接触线自身的阻尼，理论最大风偏比仿真风偏偏大。随机风速下的最大风载具有瞬时特性，对接触网具有一定的冲击作用，使接触网结构弯曲，最大偏移发生在顺风向悬挂点一侧，严重时会增加刮弓事故发生的概率，是引起接触网故障的主要原因。

文献[5]的结果显示，在接触网跨距为48 m，平均风速为20 m/s时，接触线跨中点位移振幅为116.1 mm ，最小位移为-1 mm，最大位移为115.1 mm；平均风速为30 m/s时，接触线跨中点位移振幅为203 mm，跨中点位移最小为-1 mm，最大为202 mm。文献[6]的结果显示，在接触网跨距为50 m，自然风速为20 m/s时，接触线跨中点位移振幅在150 mm，平均偏移为50 mm；自然风速为30 m/s时，接触线跨中点位移振幅为250 mm，平均偏移为100 mm。文中接触网跨距为65 m，在33 m处最大偏移为287.9 mm，最小偏移为27.5 mm，拉出值为- 4.6 mm。由于结构参数的选择不同，使得仿真结果过于保守，从图9理论结果与仿真结果对比，在误差范围内认为本文所采用的仿真模型是可信赖的。

3.2 结构参数对接触网风偏影响分析

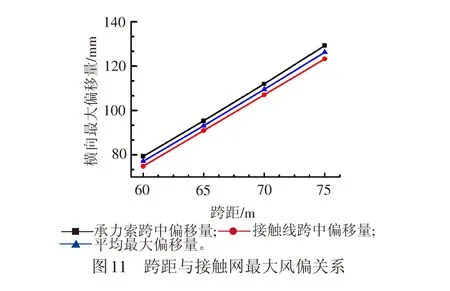
接触网结构参数、静态风方向角及风速大小是接触网横向偏移主要影响因素，接触网结构参数主要包括跨距、张力等。本文依据风偏移理论模型式(14)和式(18)计算不同风速、不同跨距及不同风向角下受风偏移量，理论受风偏移量取接触线的受风偏移量与承力索受风偏移量的平均值，结果见图10～图12。

仿真结果表明：

(1) 通过对比分析6～12级风速接触网与承力索跨中理论风偏值与跨中仿真风偏值，由于理论计算没有考虑接触网的风摆挠度，风速较大时，仿真风偏可变因素较大，具有不稳定性，与理论风偏误差相差较大，但在较低风速时，理论风偏与仿真风偏误差相对稳定。

(2) 在研究跨距对接触网风偏影响关系中，考虑风速在10级范围随跨距的增加偏移增大，跨距在60～75 m范围内时平均风偏值在50～110 mm之间。

(3) 在研究风向与接触网夹角对风偏影响关系中，由于承力索与接触线直径的不同随着风偏角度增大，接触线比承力索对风载的抗风偏能力更高。

为保证接触网在风载作用下良好的工作，接触线对受电弓中心线的受风偏移值不超过规定的最大许可值。文献[20]规定，接触线对受电弓中心的最大水平偏移值不应超过500 mm。从以上图中看出，在跨距中点有最大偏移，当平均风速为22.9 m/s时，接触网最大偏移为301.1 mm；承力索最大偏移为348.2 mm。根据结构参数对接触网风偏的影响分析，在线路设计时应该根据当地风向顺风向布线，当风速较大时减小跨距增大定位器刚度及线索的模量以减小接触网的偏移，降低发生故障的概率。

4 结论

本文采用Davenport功率谱，运用小波分析法数值模拟水平方向脉动风速时程。基于接触网模型，建立接触网横向动力学振动微分方程。在此基础上，将随机风场、平均风速及最大风速作用于接触网，分析了直线区段接触网横向风振响应及不同参数下对接触网横向风偏的影响。得到结论如下：

(1) 本文通过小波分析法准确地模拟了接触线与承力索安装高度处水平风速时程，用于对接触网横向振动特性的研究。接触网横向动力学振动研究具有可靠性。

(2) 随机风场脉动风速使接触网发生横向微幅振动，对受流过程存在安全隐患；平均风载是引起接触网横向偏移的主要因素，平均风载反映接触网风载偏移的均值，最大风载引起的接触网横向偏移是造成接触网事故的主要原因，定位器对接触网横向振动具有一定的制约。

(3) 仿真结果说明，随着风速的增大，接触网的抗风稳定性降低；接触线与承力索的材料结构不同，抗风偏能力也具有差异，结构的刚度越大抗风偏能力也越大。跨距的增大使接触网柔性增大同时降低了接触网结构的抗风稳定性，因此在增大跨距的同时应提高接触线定位器刚度及接触网的刚度。

参考文献：

[1] 周伟.风区铁路接触网风偏检测技术及数值模拟方法研究[D].湖南:中南大学,2012:1-8.

[2] 吴家岚. 高速铁路接触网风致响应分析[D].成都:西南交通大学,2011:9-16.

[3] 李荣帅,谢强,周锋,等.高速电气化铁路接触网自振特性及横向风振动力分析[J].铁道标准设计,2009(1):98-100.

LI Rongshuai, XIE Qiang, ZHOU Feng,et al. Analysis about Self-vibration Charac Teristics and Transverse Wind Vibrationof the High-speed Electrified Railway Catenary[J]. Railway Standard Design, 2009(1):98-100.

[4] 韩佳栋,曹树森,刘晓红,等.强风地区接触网风振响应分析[J].铁道建筑技术,2010(S1):207-210.

HAN Jiadong,CAO Shusen,LIU Xiaohong,et al. Wind Vibration Response Analysis of Contact Wire in the Strong Wind Area[J]. Railway Constrution Technology,2010(S1):207-210.

[5] 赵飞,刘志刚,韩志伟.随机风场对弓网系统动态性能影响研究[J].铁道学报,2012,34(10):36-42.

ZHAO Fei, LIU Zhigang, HAN Zhiwei.Simulation Study on Influence of Stochastic Wind Field to Dynamic Behavior of Pantograph-catenary System[J].Journal of the China Railway Society, 2012,34(10):36-42.

[6] 李瑞平,周宁,张卫华,等.基于AR模型的接触网脉动风场与风振响应[J].交通运输工程学报,2013,13(4):56-62.

LI Ruiping,ZHOU Ning, ZHANG Weihua,et al.Fluctuating Wind Field and Wind Induced Vibration Response of Catenary Based on AR Model[J].Journalof Traffic and Transportation Endinnering,2013,13(4):56-62.

[7] 白泉,朱浮声,边晶梅.基于正交小波逆变换的空间相关性风场数值模拟[J].四川建筑科学研究,2008,34(6):30-33.

BAI Quan,ZHU Fusheng, BIAN Jingmei. Simulation of Wind Field with Spatial Correlation Based on Orthogonal Basisinverse Wavelet Transform[J]. Sichuan Building Science, 2008, 34(6):30-33.

[8] 张文福,马昌恒,孙晓刚,等.基于小波分析的空间相关性风场模拟[J].空气动力学学报,2018,26(4):425-429.

ZHANG Wenfu, MA Changheng,SUN Xiaogang,et al. Simulation of the Spatial Correlation of the Wind Field Based on Wavelet Analysis[J]. Acta Aerody Namica Sinica,2008,26(4):425-429.

[9] 季国瑞.风电场风速软测量与预测及短期风速数值模拟方法研究[D]. 北京:华北电力大学,2009:70-81.

[10] 刘文洋,张文福.三维空间相关风场的计算机模拟及Matlab[J].空间结构,2008,14(2):14-17.

LIU Wenyang, ZHANG Wenfu.Computer Modeling on Wind Histories with Spatial Correlativity and the Program in Matlab[J].Spatial Structures,2008,14(2):14-17.

[11] 于万聚.高速电气化铁路接触网[M].成都:西南交通大学出版社,2013:20-54.

[12] 蔡成标,翟婉明.高速铁路受电弓-接触网系统动态性能仿真研究[J].铁道学报,1997,19(5):38-43.

CAI Chengbiao,ZHAI Wanming. Simulation Research of High-speed Pantograph-catenary System about Dynamic Performance[J].Journal of the China Railway Society,1997,19(5):38-43.

[13] 曲昀卿,李英辉.电气化铁路弓网系统建模与仿真分析[J].计算机仿真,2013,30(6):202-205.

QU Junqing, LI Yinghui. Modeling and Simulation Analysis of Electrified Railways Catenary-pantograph System[J].Computer Simulation, 2013, 30(6): 202-205.

[14] 梅桂明.受电弓-接触网系统动力学研究[D]. 成都:西南交通大学,2011.

[15] BENET Jesus, CUARTERO Nuria, FERNANDO Cuartero. An Advanced 3D Model for the Study and Simulation of the Pantograph Catenary System[J].Transportation Research Part C, 2013(36):138-156.

[16] 曹树森,柯坚,邓斌,等.强风地区接触网动力稳定性分析[J].中国铁道科学,2010,31(4):207-210.

CAO Shusen, KE Jian, DENG Bin, et al. The Dynamic Stability Analysis of the Catenary Systems in Strong Wind Area[J].China Railway Science,2010,31(4):207-210.

[17] 清华大学工程力学系固体力学教研组振动组.机械振动[M].北京:机械工业出版社,1980.

[18] 付秀通,詹斐生.轮/轨-弓/网系统耦合动力学数值模拟分析与研究[J].铁道学报,1998,20(3),25-32.

FU Xiutong, ZHAN Feisheng. Numerical Simulation and Experimental Studies on Coupling Dynamics of Wheel-Rail Pantograph-catenary Whole System[J].Journal of the China Railway Society,1998,20(3),25-32.

[19] 程维.电气化铁道受电弓-接触网系统受流特性研究[D].成都:西南交通大学, 2007.

[20] 中铁电气化局集团有限公司，中铁电气化勘测设计研究院.TB10009—2005铁路电力牵引供电设计规范[S].北京：中国铁道出版社，2005.