基于NPC 5电平H桥级联的牵引变电所谐波分析

何晓琼， 文德智， 秦 臻

(西南交通大学 电气工程学院， 四川 成都 610031)

随着高速、重载铁路的发展和推广，既有牵引供电系统存在一系列如电压不平衡、无功和谐波、供电能力受限等不可忽略的问题[1-4]。我国研制了世界首套基于平衡变压器和动态补偿装置(APC)的同相供电装置，较好地解决了电能质量问题，使电分相数减半，并且非常适合对既有线路的改造，但仍存在过分相问题[5-7]。基于此，文献[8]研究的基于三相-单相变换器的贯通式牵引供电系统，可完全取消电分相装置，但此供电方案仍存在局限：单相变换器输出侧还需接滤波电路，需配备单相升压变压器，牵引变电所容量受限等。

文献[9]提到的基于二极管钳位(NPC)5电平H桥(简称5H桥)级联结构的三相-单相变换器的贯通式牵引供电系统(见图1)，可取消牵引变电所输出变压器，提升变电所容量。且由于多电平逆变器级联，增加等效开关频率，总谐波含量(THD)大幅减小[10]，进而可取消滤波器，减小变电所体积。

但是，由于采用电力电子变换器，输出电压不可避免包含与开关频率相关的特征次谐波，并网时有可能与牵引网分布电感、电容以及机车负载参数匹配，导致牵引网谐振[11-13]。因此，有必要对此级联结构的输出谐波特性进行研究。另外，合适的调制策略对提升输出电压质量及推导电压谐波特性至关重要。载波移相CPS-SPWM(Carrier Phase Shifted SPWM)由于等效开关频率高，降低了总谐波含量，在高压大功率场合得到广泛应用[10,14]。本文采用CPS-SPWM作为调制策略，基于双边傅里叶函数推导了5H桥级联结构的输出谐波特性，利用Matlab/Simulink仿真平台完成仿真验证，为后期研究该牵引变电所并网及车网耦合后牵引供电系统的性能特征提供借鉴。

1 5H桥原理及CPS-SPWM调制策略

图1为基于5H桥级联的贯通式牵引供电系统，其由三相电网供电，经多绕组变压器将网侧电压转换为电力电子变换器工作电压，单相变换器级联升压为牵引网所需电压等级。根据当前IGBT发展水平，选择5个5电平H桥级联结构不仅满足牵引网要求的电压等级，还可提供比传统牵引变电所更大的容量。

考虑在各逆变结构直流侧母线电压恒定前提下，整流器部分可等效为恒定直流电压源，则变电所逆变部分可简化为以5H桥(见图2)为基本单元的级联结构。5H桥因采用二极管钳位结构可得多电平输出，其1个桥臂由3 对钳位二极管和4组互补开关构成，分别为(Sa1，Sa5)、(Sa2，Sa6)、(Sa3，Sa7)、(Sa4，Sa8)，1个5H桥理论上可得到9电平输出波形。

调制方面采用CPS-SPWM调制策略，1个桥臂上对4 组开关控制得到5电平PWM电压波形。控制中用1个正弦调制波和4 个相角差为π/2的同频三角载波比较，得到4 路PWM(PWM1—PWM4)信号，用于控制上半桥臂4 个IGBT。再对各路PWM取反得到其互补开关的PWM(-PWM1—-PWM4)信号，用于控制下半桥臂4 个IGBT，见图2。由这8 路PWM信号共同完成对1个桥臂的控制。

给予不同的开关通断信号，得到输出电平也不同，表1给出了开关通断与输出电压电平关系，其中“1”表示通，“0”表示断，Vdc为直流电压。由表1可知，分配电平时应遵循改变最少个数开关以实现输出电平改变0的原则。5H桥的B桥臂控制同理：CPS-SPWM调制下，B桥臂的初始载波相角与A桥臂相差π/4，四路PWM载波依次移动π/2。通过三角载波移相，使得5H桥两桥臂输出的PWM脉冲在相位上错开，从而使5H桥输出电压最多有9 个电平。

表1 开关模态与输出电压电平关系

变电所的级联结构为串联的5 个5H桥，5H桥间的初始载波相位依次移动2π/5，理论上可得41 个电平输出电压波形，且等效开关频率是1 个5H桥的5倍，总谐波含量大大减小。

2 5H桥谐波特性分析

1个2电平桥臂输出电压PWM波形的双边傅里叶函数表达式为[14]

( 1 )

式中:第一项为基波项；第二项为载波谐波项；第三项为载波谐波上下边频。m表示m倍于载波频率的载波谐波；n=±1, ±2, …表示某次载波谐波的上下边频；Ed为5H桥直流电压；α为三角载波初始相角；φ为正弦波初始相角；Jn为贝塞尔函数；M为幅值调制度，M=Vs/Vc，其中，Vc为三角载波幅值，Vs为调制波幅值；F为频率调制比，F=ωc/ωs=fc/fs(F取整)，其中，fc为三角载波频率，fs为调制波频率，ωc为三角载波角频率，ωs为调制波角频率。

1个5H桥桥臂(设为A桥臂)载波C1～C4的相角依次移动π/2，再结合两电平uao的表达式，可得5H桥1 个桥臂上4 个PWM波形的双边傅里叶函数的表达式

( 2 )

同理推导出其余3 个PWM波形表达式，并由上式可知，uai(t)是关于ωst和α的函数，因此其余3 个PWM波形可表示为

( 3 )

ua3(t)=ua1(ωst,α0+π)

( 4 )

( 5 )

由叠加原理可得A桥臂输出电压为

( 6 )

对式( 6 )进行简化,结合Matlab得计算结果见图4。当m为4的整数倍数时，“[ ]”中求和项的值为4e-jma；当m不为4整数倍数时，此项值为0。

( 7 )

对于5H桥的B桥臂，其初始三角载波相位相对桥臂A滞后π/4，并且调制波为-us(t)，推导过程同式( 1 )～式( 7 )，则uB(t)在CPS-SPWM调制下的双边傅里叶函数表达式为

( 8 )

两桥臂输出电压差即为5H桥的输出电压uAB(t)，再对表达式进行简化，得5H桥输出电压uAB(t)为

uAB(t)=uA(t)-uB(t)=MEdsin(ωst)+

( 9 )

此式表明，5H桥在CPS-SPWM调制下具有较为理想的谐波特性：不存在载波谐波项；仅包含8的整数倍载波频率的上下边频中的奇数次谐波，不存在8倍载波频率以下的载波谐波及其上下边频。

3 新型牵引变电所输出谐波特性分析

级联结构中的5H桥之间采用移相控制，5H桥内的两桥臂仍然按照载波相角差为π/4的CPS-SPWM进行控制。为得到级联叠加的最多电平数，5H桥之间三角载波相位按2π/N(N为5H桥个数)移相。由此可得文中提到的5 个5H桥级联结构(N=5)中，相邻10个桥臂的初始三角载波相位关系,见图5。图中C5H-11表示级联的5H桥的A桥臂初始三角载波，C5H-21表示级联的5H桥的B桥臂初始三角载波。

结合式( 9 )， 5 个5H桥级联结构的输出电压可叠加求和得

e-jmα1+e-jmα3+e-jmα5+e-jmα7+e-jmα9·

(10)

由于相邻5H桥之间的初始载波的相位相差2π/5，则上式“[ ]”中求和项可进行简化：当m=5k，k=1,2,…时，该项的值为5；当m≠5k，该项的值为0。因此，式(10)最终表达式为

us(t)=5MEdsin(ωst)+

(11)

由式(11)可知，5 个5H桥的级联结构，输出电压谐波特性如下：不存在载波谐波项；仅包含40的整数倍载波频率的上下边频中的奇数次谐波，不存在其以下的载波谐波及其上下边频；输出电压幅值增大至5倍，因此可通过改变级联的5H桥个数和调制度M，改变输出电压幅值。

通过对式(11)的推导，可总结出p个5H桥级联输出电压的一般表达式

us(t)=pEdsin(ωst)+

(12)

4 仿真和实验验证

在Matlab/Simulink平台上搭建5个5H桥级联模型，仿真结构见图6，母线直流电压用直流电压源代替，采用电感式均压电路对直流侧均压。元器件参数及控制参数见表2。运行仿真模型得到仿真结果见图7、图8。

表2 仿真参数说明

名称数值直流电容C1～C4/mF20直流侧母线电压/kV6．6调制波频率/Hz50调制度0．95载波频率/Hz500～3000仿真步长10-6仿真时间/s0．05

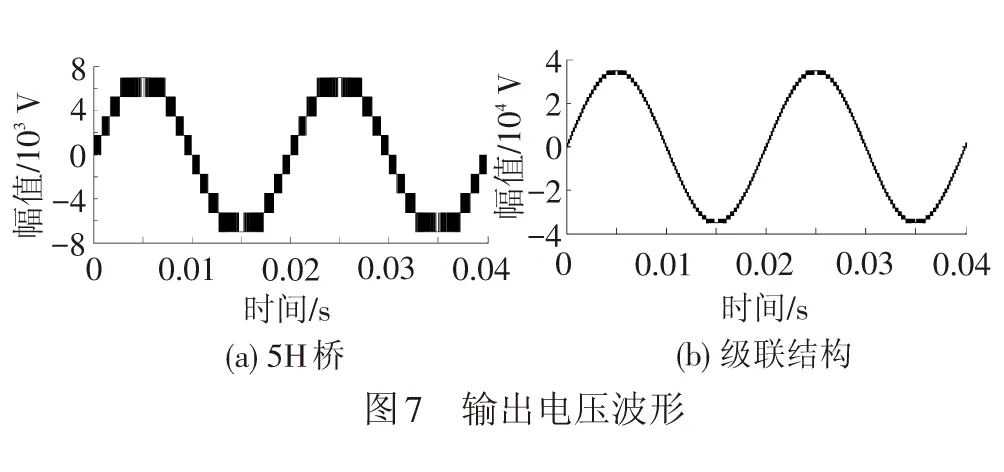
由图7(a)、7(b)可知,CPS-SPWM调制下的5H桥及级联结构输出电压电平数分别为9电平、41电平，达到预期效果，且级联结构的输出表现出较好的正弦性。

由图8(a)可知，CPS-SPWM调制下的5H桥输出电压总谐波失真率(THD)为13.7%，谐波具有明显分布规律：仅包含8的整数倍载波频率的上下边频，随着谐波次数越高，频带越宽且谐波含量越低；由图8(b)可知，5 个5H桥级联之后谐波得到极大改善，THD为2.8%，满足公用电网谐波标准[15]，仅包含40的整数倍载波频率的上下边频。

FFT分析结果中偶次谐波含量≤0.05%，与理论分析对应。因此表3主要统计了载波频率为3 000 Hz时，5H桥输出电压谐波中，8fc、16fc、24fc及32fc次谐波的上下频带各奇次谐波含量；表4统计了级联结构输出电压谐波中，40fc、80fc、120fc及160fc次谐波的上下频带各奇次谐波含量。数据表明：特征次谐波主要分布在上述边频中的奇数次谐波，并且含量符合式( 9 )、式(11)谐波特性，验证了推导的正确性。

表3 5H桥输出电压特征次谐波含量表

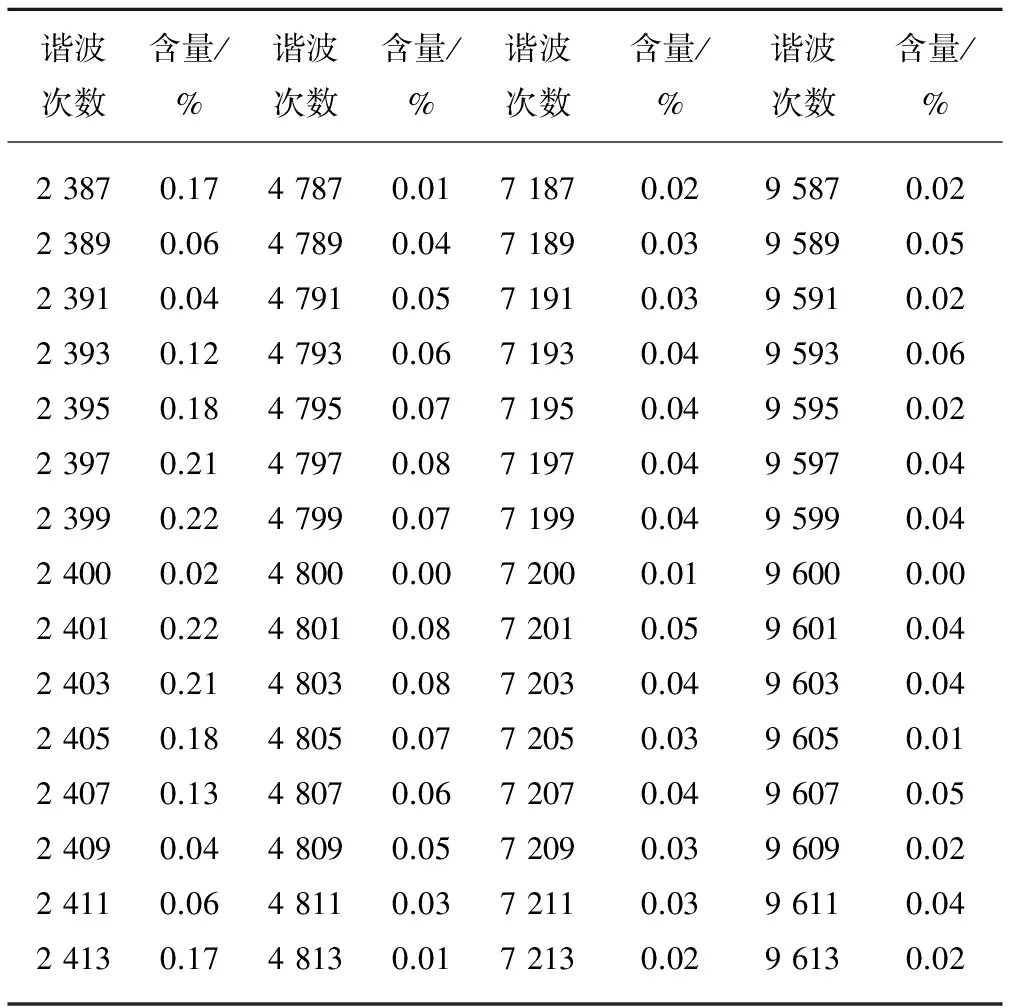
表4 级联结构输出电压特征次谐波含量表

本文搭建了2个5H桥级联的小功率实验平台，见图9。实验平台主要由控制板、采样板、IGBT板连接的主电路，以及驱动电源和独立直流电源构成。控制板核心处理芯片采用Altera公司生产的EP3C55F484C8第三代cyclone FPGA。直流侧为48 V独立直流电源，调制波频率为50 Hz，载波频率设定为0.5 kHz，调制度为0.87。

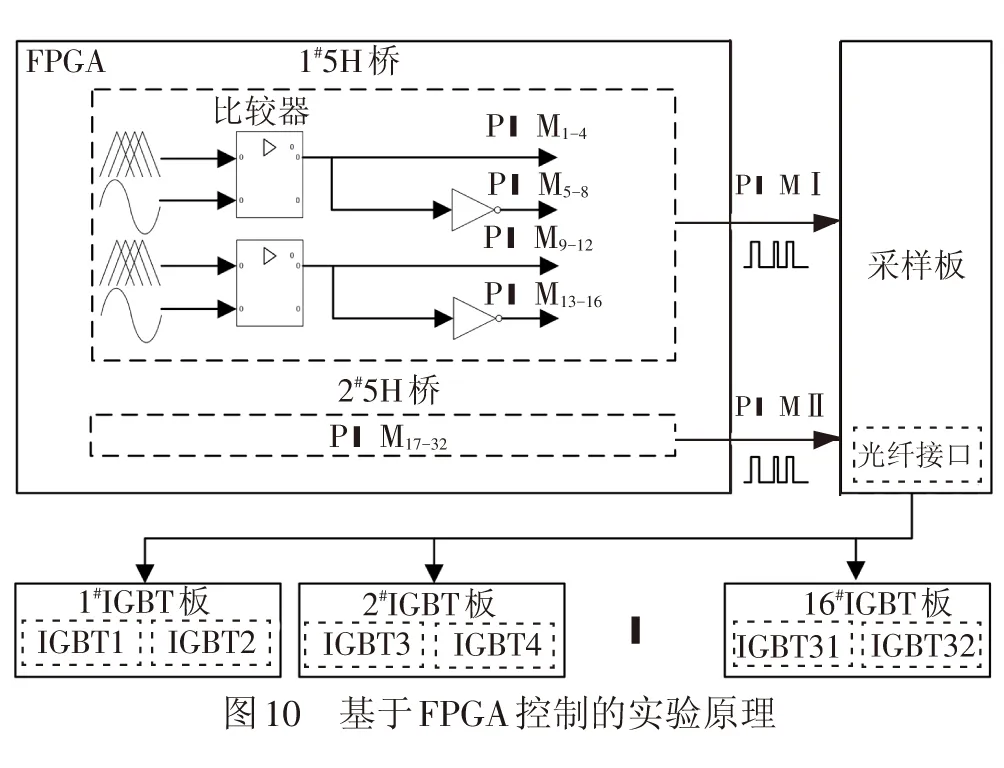
基于FPGA控制的实验原理见图10。通过Verilog HDL编程，FPGA由调制算法产生32路IGBT驱动信号，经过采样板光纤接口传输至对应IGBT板，再经过板上驱动电路驱动相应IGBT。对单个5H桥及2个5H桥级联系统输出电压分别作FFT分析，实验结果见图11。由此可以验证式( 9 )、式(12)推导结果的正确性。

5 结论

本文首次分析了基于5H桥级联的新型牵引变电所输出谐波特性，利用双边傅里叶函数推导了CPS-SPWM调制下的5H桥及其级联结构输出谐波分布，完成了5个5H桥级联系统的仿真和2个5H桥级联系统的小功率实验。仿真和实验结果表明：

(1) 5H桥的输出电压具有较为理想的谐波特性：不存在基波谐波项，仅包含8的整数倍载波频率上下边频中的奇数次谐波；不存在8倍载波频率以下的载波谐波及其上下边频。

(2) 5个5H级联结构的输出电压不存在基波谐波项；载波谐波部分仅包含40的整数倍载波频率上下边频中的奇数次谐波；且总输出谐波含量满足国标。

由于采样板光纤接口数量和实验经费等限制，暂时只完成2个5H桥级联结构的实验，以验证理论分析。在后续完成对采样板硬件电路的改进，增加光纤通道数量后，将继续完成5个5H桥级联系统实验。

本文的研究成果可以为后期研究变电所并网及车网耦合后牵引供电系统的性能特征提供借鉴。

参考文献：

[1] CHEN S L, LI R J, HIS P H. Traction System Unbalance Problem-analysis Methodologies[J]. IEEE Trans on Power Delivery, 2004, 19(4): 1 877-1 883.

[2] 李群湛. 牵引变电所供电分析及综合补偿技术[M]. 北京:中国铁道出版社, 2006.

[3] 张丽艳. 新建电气化铁路对电网电能质量影响的预测与对策分析研究[D]. 成都: 西南交通大学, 2012.

[4] 周福林, 李群湛, 邱大强. 基于混合补偿的同相牵引供电系统[J]. 铁道学报, 2012, 34(1): 19-23.

ZHOU Fulin, LI Qunzan, QIU Daqiang. Co-phase Traction Power Supply System Based on Hybrid Compensation[J]. Journal of the China Railway Society, 2012, 34(1): 19-23.

[5] SHU Z, XIE S, LU K. Digital Detection, Control and Distribution System for Co-phase Traction Power Supply Application [J]. IEEE Transactions on Industrial Electronics, 2012, 9(1): 1-9.

[6] 王庆贤,左晓薇,李少帅,等. 同相供电系统改进型综合补偿电流检测方法研究[J]. 铁道学报,2013,35(2):26-31.

WANG Qingxian, ZUO Xiaowei, LI Shaoshuai, et al. Research on Improved Comprehensive Compensation Current Detection Method by Co-phase Power Supply System[J]. Journal of the China Railway Society, 2013,35(2):26-31.

[7] 夏焰坤,李群湛,解绍锋,等. 电气化铁道贯通同相供电变电所控制策略研究[J]. 铁道学报,2014,36(8):25-31.

XIAYankun, LI Qunzhan, XIE Shaofeng, et al. Study on Control Strategy of Continuous Co-phase Power Supply Substations of Electrical Railways[J].Journal of the China Railway Society, 2014,36(8):25-31.

[8] HE Xiaoqiong, SHU Zeliang, PENG Xu, et al. Advanced Co-phase Traction Power Supply System Based on Three-phase to Single-phase Converter[J]. IEEE, Transactions on Power Electronics, 2013, 29(10):5 323-5 333.

[9] 周瑛英, 何晓琼, 舒泽亮. 基于三相-单相变换器的级联型无输出变压器的牵引供电系统研究[C]//第八届中国高校电力电子与电力传动学术年会论文集. 武汉: 中国高校电力电子与电力传动组委会, 2014.

[10] 李建林, 李晶, 王立乔, 等. CPS-SPWM在级联型有源电力滤波器中的应用[J]. 电力系统自动化, 2006, 30(9): 64-68.

Ll Jianlin, LI Jing, WANG Liqiao, et al. Carrier Phase Shifted SPWM and Its Applications in Shunt APF[J]. Automation of Electric Power Systems, 2006, 30(9):64-68.

[11] 郎兵, 吴命利. 牵引网谐波模型及其仿真计算[J]. 电力系统自动化, 2009, 33(17):76-80.

LANG Bing, WU Mingli. Harmonics Model of Traction Network and Its Simulation[J]. Automation of Electric Power Systems, 2009, 33(17):76-80

[12] 何正友, 胡海涛, 方雷, 等. 高速铁路牵引供电系统谐波及其传输特性研究[J]. 中国电机工程学报, 2011,31(16): 55-62.

HE Zhengyou, HU Haitao, FANG Lei, et al. Research on the Harmonic in High-speed Railway Traction Power Supply System and Its Transmission Characteristic[J]. Proceedings of the CSEE, 2011, 31(16): 55-62.

[13] 崔恒斌, 冯晓云,林轩, 等. 车网耦合下高速铁路牵引网谐波谐振特性研究[J]. 电工技术学报, 2013, 28(9): 55-64.

CUI Hengbin, FENG Xiaoyun, LIN Xuan, et al, Research on Harmonic Resonance Characteristic of High-speed Railway Traction Net Considering Coupling of Trains and Traction Nets [J]. Transactions of China Electro-technical Society, 2013, 28(9): 55-64.

[14] 刘凤君. 环保节能型H桥及SPWM直流电源式逆变器[M]. 北京: 电子工业出版社, 2010.

[15] 国家电力工业部(原能源部). GB 14549—93 电能质量-公用电网谐波[S]. 北京: 中国电力出版, 1993.