基于云模型和不确定AHP的列控运营安全评估

郭荣昌， 陈光武， 赵小娟， 火久元， 范多旺

(1. 兰州交通大学 自动控制研究所， 甘肃 兰州 730070； 2. 兰州交通大学 甘肃省高原交通信息工程及控制重点实验室， 甘肃 兰州 730070； 3. 兰州交通大学 电子与信息工程学院，甘肃 兰州 730070)

列车运行控制系统是高铁中的核心装备和安全相关系统，能控制列车运行间隔，防止超速，保证列车正点高效运行[1,2]。列车运行控制系统的安全状态对行车安全具有重要的影响。

目前国内在高铁安全标准转化、安全评估与认证体系、概率安全、安全管理等方面做了大量研究[3-8]，而在列控运营安全方面的研究较少。已有的列控运营安全相关的研究主要是从多级可拓评价[9]和复杂网络[10]的角度进行。多级可拓评价方法局限于评估技巧的改进，很少从安全的模糊性和随机性等本质属性上进行评估。复杂网络方法的核心思想是将列控系统看成一个复杂网络，采用涌现理论和熵理论对安全进行安全评估，其关键在于安全要素网络和涌现机制的构建，而目前现有的安全要素网络和涌现机制都不够完善，并且复杂网络方法需要大量数据，这也影响了此类方法的推广应用。

云模型是研究定性概念和定量数值之间相互转换的不确定性认知模型，具有非常好的处理模糊性和随机性的能力[11-13]。为了解决上述问题，考虑到列控运营安全的模糊性和随机性，本文引入了云模型和不确定层次分析法AHP(Analytic Hierarchy Process)对列控运营安全进行评估。首先建立了列控运营安全评估体系；其次采用不确定AHP计算评估体系的权重区间，利用集对分析理论得到权重精确值；然后给出了基于云模型的列控运营安全评估方法；最后以实例表明了评估方法的有效性。

1 列控运营安全评估体系

列控安全评估涉及很多影响因素，且各个因素影响程度均不相同，只有综合考虑各种因素，才能够反映列控运营的整体安全状态。然而由于技术水平的限制，很难对所有的因素进行信息采集。此外，不同运行条件也对列控运营的安全状态造成差异。因此本文借鉴已有的工作，覆盖人、机、环、管四方面，依据科学性、代表性原则，构建列控运营安全评估指标体系见图1。

指标体系由目标层、项目层和指标层3个层次构成。U是目标层，表示列控运营安全状态的评估结果；U1，U2，U3，U4构成项目层，表示列控运营状态的安全评估因素，是从不同方面对目标层的具体描述；指标层是项目层的细化，表示具体的评估状态量。

2 安全评估体系权重计算

2.1 采用不确定AHP计算指标体系的权重区间

安全评估体系权重的计算是列控安全运营评估的1个难点。不确定AHP采用的是区间标度，可以很好地反映专家对指标体系主观判断的模糊性[14]，因此，采用不确定AHP来描述专家对各安全因素之间相对重要度的评估，具体步骤如下:

Step1计算区间数判断矩阵

不失一般性，假设指标体系某级有n个安全因素，各专家采用1～9标度法对安全因素之间的相对重要度进行评估；之后将专家意见进行综合，得到区间数判断矩阵

A=Aijn×n=[aij,bij]=

( 1 )

式中:aij、bij为评判区间的上下限。

Step2计算权重区间

依据判断矩阵A得到一致性逼近矩阵M=(mij)n×n，有

( 2 )

计算一致性逼近矩阵M的权重Wiw1,w2,…,wn，有

( 3 )

计算出权重Wiw1,w2,…,wn后，计算极差矩阵ΔM1、ΔM2，权重传递误差ΔkWj，有

( 4 )

式中：k=1,2。

区间数判断矩阵A的权重区间为

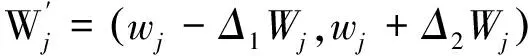
( 5 )

2.2 利用集对分析计算权重精确值

μj=aj+bji+cjj

( 6 )

式中:i、j为差异度和对立度系数;aj=wj-Δ1Wj，bj=Δ1Wj+Δ2Wj，cj=1-wj-Δ2Wj。

分别计算出确定性区间相对权重Pj和不确定性相对权重Qj，有

( 7 )

( 8 )

3 基于云模型的安全评估方法

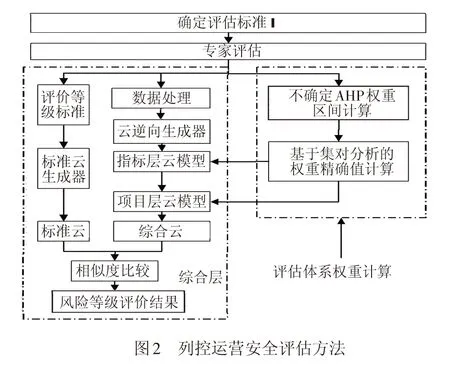
评估方法模型见图2，基于云模型的安全评估主要步骤为:

Step1确定安全评估等级S；

Step2邀请专家进行评估，并对专家评价信息进行预处理；

Step3依据安全评估等级生成标准云；

Step4将安全评估的信息生成指标层云模型；

Step5指标层云模型经过综合得到项目层云模型，项目层云模型经过综合得到综合云；

Step6对标准云和综合云进行相似度计算，取相似度最大的标准云等级为安全评估等级。

3.1 确定安全评估等级S

建立风险严重度等级S={S1,S2,…,SP}，P为列控运营安全等级个数。

3.2 专家评价

邀请专家对指标体系U的项目层和指标层中的指标进行评价，评价值在[0,1]之间，0为最不安全，1为最安全。

3.3 安全评估标准云设计

Step1根据区间的上下限值，计算期望Exi为

( 9 )

Step2由于安全评估中各个等级的评价边界值是两个级别相互过渡的临界值，所以该评估域的边界值应该属于与其相邻的两个级别，即为

(10)

Step3计算Hei=η。η为常数，其取值大小反映安全评估标准云评估标准的随机性大小。η越大，评估标准的随机性越大，评估标准越难以确定，故其取值不宜太大。

3.4 指标层云模型

对专家评价结果Xij(xi1j,xi2j,…,xiMj)进行处理，其中i为项目层因素Ui的序号，M为Ui对应指标层评估因素的个数，j=1,2,…,J；计算得到M个评估云模型Cim(Exim,Enim,Heim)，其中m=1,2,…,M；Exim是Cim期望；Enim是Cim的熵；Heim是Cim的超熵。计算步骤如下：

Step1Cim的期望为

(11)

Step2Cim的熵为

(12)

Step3Cim的超熵为

(13)

3.5 项目层云模型和综合云计算

计算出指标层云模型之后，根据云的数字特征和对应的权重计算出对应的项目层云模型为

Ci=(EXi,ENi,HEi)

(14)

计算出项目层云模型之后，再根据式(14)，计算得到综合云模型CZ(EXZ,ENZ,HEZ)。

3.6 云相似度计算和运营风险等级确定

分别计算综合云相对于各个标准云的相似度，取相似度最大的标准云等级为列控运营安全评估等级。相似度的定义和计算步骤见文献[16]。

4 实例验证

以兰新高铁某段CTCS-3级列控系统为研究对象，采用本文提出的评估方法对运营安全进行评估。

4.1 评估体系权重计算

(1) 计算权重区间

以项目层指标U4说明计算过程。邀请10个专家对项目层指标U4对应的指标层因素U41、U42、U43和U44进行两两比较，专家经过商讨，得到判断矩阵为

依据式( 3 )～式( 5 )，计算得到U41、U42、U43和U44的权重区间为

W′=([0.433 4,0.576 2]，[0.240 3,0.382 2]，[0.139 5,0.214 4]，[0.047 2,0.057 8])

(2) 计算精确权重值

μ1=0.433 4+0.142 8i+0.423 8j

μ2=0.240 3+0.141 9i+0.617 8j

μ3=0.139 5+0.074 9i+0.785 6j

μ4=0.047 2+0.010 6i+0.942 2j

根据式( 7 )，计算得到

Pj=[0.428 2,0.297 6,0.169 3,0.050 3]

Qj=[0.236 2,0.236 6,0.254 9,0.272 5]

依据式( 8 )，计算得到U41、U42、U43和U44的精确权重值

(3) 计算体系权重值

同理，计算得到

4.2 确定安全评估等级S

参考EN50126标准[17]和已有的研究成果，将列控运营安全等级分为4级，分别为：Ⅰ级，安全水平不可接受，必须采取措施降低风险；Ⅱ级，安全水平不理想，当风险降低不可行时，需要在铁路组织同意下接受风险；Ⅲ级，安全水平可以容忍，风险可以被合理控制；Ⅳ级，安全水平高，风险可以忽略。所以，安全评估等级S={Ⅰ,Ⅱ，Ⅲ，Ⅳ}。

4.3 专家评估

邀请10位列控运营安全方面的专家对该高铁列控的运营安全进行评估。评估按照评估体系进行分层打分，打分分值在[0,1]范围之内，0表示安全等级为Ⅰ级，1表示安全等级为Ⅳ级。

4.4 计算标准云

依据评价集S={Ⅰ，Ⅱ，Ⅲ，Ⅳ}，按照等分原则将安全区间[0,1]分为4个子区间，分别为：[0,0.25)(Ⅰ级)，[0.25,0.5](Ⅱ级)，[0.5,0.75)(Ⅲ级)，[0.75,1](Ⅳ级)。依据经验取常数η为0.025，可由式( 9 )、式(10)，计算出评价标准云为：Ⅰ级标准云CⅠ(0,0.106 2,0.025)，Ⅱ级标准云CⅡ(0.375,0.106 2,0.025)，Ⅲ级标准云CⅢ(0.625,0.106 2,0.025)，Ⅳ级标准云CⅣ(1,0.106 2,0.025)。采用正向云生成器可生成评价标准云见图3。

4.5 指标层云模型

以指标层因素U22为例，说明指标层云模型的计算过程。

10位专家对铁路运输服务影响属性的评价结果为X22j=(0.63,0.76,0.67,0.85,0.81,0.87,0.73,0.63,0.75,0.85)。

将X22j代入式(11)～式(13)，计算得到Ex22=0.73，En22=0.45，He22=0.012。所以，指标层因素U22的云模型C22(Ex22,En22,He22)为(0.73,0.45,0.012)。同理，分别计算指标层其他因素的云模型，得到表1。

表1 指标层云模型

4.6 项目层云模型和综合云模型

4.7 计算相似度

采用MATLAB 6.0计算相似度，得到综合云C和标准云的相似度δ(δ1,δ2,δ3,δ4)为(0.010,0.103,0.424,0.463)。从结果看出，综合云C和Ⅳ级标准云的相似度最大，所以运营安全评估等级为Ⅳ级；但由于综合云C和Ⅲ级标准云的相似度δ3的大小和δ4相差不大，也可认为安全评估处于Ⅲ级和Ⅳ级之间，更靠近Ⅳ级。所以评估结果为存在少许风险，但存在的风险可以被合理控制，基本可以认为风险可以忽略不计。安全评估结果与现场情况相同，这说明评估结果合理，也证明了本文方法的正确性和有效性。画出综合云C(红色部分)与标准云(黑色部分)的图形见图4。从图可见，综合云介于Ⅲ级和Ⅳ级标准云之间，但是更靠近Ⅳ级，这与相似度计算结果相同。

5 结论

在研究列控运营安全评估理论和技术的基础上，本文将不确定AHP、集对分析理论和云模型理论引入到列控运营安全评估之中，并用实例进行计算和验证，得到以下结论：

(1) 利用不确定AHP确定了安全评估体系的权重区间，符合专家的工程实践和思维决策。通过集对分析将权重区间转化为权重精确值，使得计算结果更加科学合理。

(2) 利用云模型较好地处理模糊性和随机性的能力，建立了标准云模型、指标层云模型和综合云模型，兼顾了安全评估中的不确定性和随机性。

(3) 最后通过实例验证了基于云模型和不确定AHP在列控运营安全评估中应用的可行性和有效性。

本方法从风险本质属性模糊性和随机性的角度出发，客观科学的评估了列控运营安全的等级，为现场列控运营的安全评估提供了更加科学的方法，具有良好的应用价值。同时，本文中的评估方法也可以应用于其他安全评估领域。

参考文献：

[1] 宁滨，唐涛，李开成，等. 高速列车运行控制系统[M].北京：科学出版社, 2012.

[2] 郭进，张亚东. 中国高速铁路信号系统分析与思考[J].北京交通大学学报, 2012, 36(5):90-94.

GUO Jin, ZHANGYadong. Study and Consideration on Chinese High Speed Railway Signal System[J]. Journal of Beijing Jiaotong University, 2012, 36(5): 90-94.

[3] 燕飞，唐涛. IEC61508及其在铁路安全相关系统研制开发中的应用研究[J].铁道学报, 2005, 27(3): 124-128.

YAN Fei, TANG Tao. Study on IEC61508 Application in Railway Safety Related System[J].Journal of the China Railway Society, 2005, 27(3): 124-128.

[4] 郜春海，燕飞，唐涛. 轨道交通信号系统安全评估方法研究[J]. 中国安全科学学报, 2005, 15(10): 78-83.

GAO Cunhai, YAN Fei, TANG Tao. Study on Safety Assessment of Rail Traffic Signaling system[J].China Safety Science Journal, 2005, 15(10): 78-83.

[5] 刘超，唐涛，李开成. 高速铁路信号系统的安全管理评价研究[J].中国安全科学学报, 2013, 23(1):129-135.

LIU Chao, TANG Tao, LI Kaicheng. Research on Assessing Safety Management of High Speed Railway Signal System[J]. China Safety Science Journal, 2013, 23(1): 129-135.

[6] 肖雪梅，王艳辉，张思帅，等. 基于耗散结构和熵的高速铁路事故演化机理研究[J]. 中国安全科学学报, 2012, 22(5): 99-105.

XIAO Xuemei, WANG Yanhui, ZHANG Sishuai, et al. Evolution Mechanism of High Speed Railway Accident Based on Dissipative Structure and Entropy Theory[J]. China Safety Science Journal, 2012, 22(5): 99-105.

[7] 刘敬辉，戴贤春，郭湛，等. 铁路系统基于风险的定量安全评估方法[J]. 中国铁道科学, 2009, 30(5): 123-128.

LIU Jinghui, DAI Xianchun, GUO Zhan, et al. Quantitative Safety Assessment Method Based on Risk in Railway System[J]. China Railway Science, 2009, 30(5): 123-128.

[8] 王欣，左忠义. 基于系统动力学的高铁安全管理研究[J]. 中国安全科学学报, 2013, 23(10): 158-163.

WANG Xin, ZUO Zhongyi. Research on High Speed Rail Safety Management Based on System Dynamics[J]. China Safety Science Journal, 2013, 23(10): 158-163.

[9] 张亚东，郭进，戴贤春，等. 基于多级可拓评价法的列车运行控制系统运营安全风险评价[J]. 中国铁道科学, 2013, 34(5): 114-119.

ZHANG Yadong, GUO Jin, DAI Xianchun, et al. Operation Safety Risk Evaluation of Train Control System Based on Multilevel Extensible Evaluation Method[J]. China Railway Science, 2013, 34(5): 114-119.

[10] XIAO Xuemei, WANG Yanhui, JIA Limin. Hierarchical Network Model of Safe High-speed Rail Operation[J]. Transportation Research Record: Journal of the Transportation Research Board, 2011(2261): 49-56.

[11] 姚文斌，王真，赵玲，等. 基于云模型的灾难恢复能力评价方法研究[J].计算机科学,2015, 42(8): 152-156.

YAO Wenbin, WANG Zhen, ZHAO Ling, et al. Study on Disaster Recovery Capability Evaluation Approach Based on Cloud Model[J]. Computer Science, 2015, 42(8): 152-156.

[12] 刘延华，陈国龙，吴瑞芬. 基于云模型和AHP的网络信息系统可生存性评估[J]. 通信学报, 2014, 35(8): 107-115.

LIU Yanhua, CHEN Guolong, WU Ruifen. Survivability Evaluation of Network Information System Based on the Cloud Model and Analytic Hierarchy Process[J]. Journal on Communications, 2014, 35(8):107-115.

[13] 苏兆品，张婷，张国富，等. 基于云模型和模糊聚合的应急方案评估[J].模式识别与人工智能, 2014, 27(11): 1 047-1 056.

SU Zhaopin, ZHANG Ting, ZHANG Guofu, et al. Evaluation of Emergency Disposal Schemes Based on Cloud Model and Fuzzy Aggregation[J].Pattern Recognition and Artificial Intellgence, 2014, 27(11):1 047-1 056.

[14] 俞素平，李素梅. 基于集对分析的隧道设计安全风险评估研究[J]. 重庆交通大学学报:自然科学版, 2014, 33(4): 38-43.

YU Suping, LI Sumei. Security Risk Assessment of Tunnel Design Based on Set Pair Analysis[J]. Journal of Chongqing Jiaotong University:Natural Science,2014, 33(4): 38-43.

[15] 施志坚，王华伟，王祥. 基于多元联系数集对分析的航空维修风险态势评估[J]. 系统工程与电子技术, 2016, 38(3):588-594.

SHI Zhijian, WANG Huawei, WANG Xiang. Risk State Evaluation of Aviation Maintenance Based on Multiple Connection Number Set Pair Analysis[J]. Systems Engineering and Electronics, 2016, 38(3): 588-594.

[16] 张仕斌，许春香. 基于云模型的信任评估方法研究[J].计算机学报, 2013, 36(2):422-431.

ZHANG Shibin, XU Chunxiang. Study on the Trust Evaluation Approach Based on Cloud Model[J]. Chinese Journal of Computers, 2013,36(2):422-431.

[17] European Committee for Electro Technical Standardization. EN 50126 Railway Application-the Specification and Demonstration of Reliability, Availability Maintainability and Safety (RAMS)[S].Brussels: European Committee for Electro Technical Standardization, 1999.