多列车多停站方案条件下高速铁路票额分配研究
赵 翔, 赵 鹏, 李 博
(北京交通大学 交通运输学院, 北京 100044)
票额分配是在一定席位能力条件下以客流需求为基础,合理设置各路径(OD)票额数量以提高客座率和客票收益的售票方法。高速铁路若采用先到先得的售票原则会引起因短途旅客购票而长途旅客无法购买到所需车票,造成部分区段客票紧张和部分区段席位虚糜并存的现象,不利于高速铁路客座能力的利用和客票收益的提高,票额分配是避免上述问题的有效手段。精准的客流预测是票额分配的前提,但客流需求具有随机性和时变性,预测结果的精度难以保证,同时高速铁路旅客运输是多区段、多OD需求、多列车、多停站方案的复杂问题,如何在非确定性需求情况下合理分配票额是提高运输收益的主要难题之一。
航空领域最早开始利用收益管理概念研究席位利用问题,也取得一系列研究成果。高速铁路旅客列车票额分配问题可以借鉴航空运输的席位控制模型,但是高速铁路旅客列车票额分配所涉及OD更多,各客流区段之间关联性更强,停站方案更复杂,因此难以照搬航空领域的研究成果。由于各国铁路运营方式不同,对席位控制问题的关注点也不尽相同。文献[1]用确定的线性模型和概率非线性模型研究了意大利铁路席位控制问题,提出铁路席位控制问题是一个多区段、单一票价的收益管理问题,文中假设需求是连续独立的随机变量,采用非嵌套席位控制方法。文献[2]研究了两等级票价、多区段、单列旅客列车的席位控制问题。文献[3]建立了考虑上座率、收益和旅客公平的铁路收益管理模型,并通过日本铁路的实例对该模型进行验证。文献[4]对印度铁路旅客列车的超售问题进行研究。国内专家学者对适用于我国国情的票额分配方法进行了探究。文献[5]以直接人公里数最大为目标,在确定性需求条件下研究多列站站停旅客列车的票额分配方法。文献[6]建立了列车席位控制和发车间隔同时优化的数学模型,研究多区段、多车次、站站停旅客列车的票额分配方法。文献[7]以单列旅客列车的预测客流为基础,以旅客列车全程的客座率、收入以及整体效益最大为目标,提出先长途后短途、先有座后无座等旅客列车票额分配的主要原则,并给出票额分配的具体算法。文献[8]以已知的独立正态分布需求为基础,研究两级票价、嵌套式、多区段、单列车的票额分配方法,以及旅客buy-up行为对票额分配的影响。文献[9]通过对需求情景进行模拟,研究了嵌套式、多区段、单列车的票额分配方法。文献[10]对比了非嵌套式票额控制、嵌套式票额控制、投标价格控制三种票额分配方法,对适合我国国情的多区段单列旅客列车票额分配方法进行了探究。文献[11]通过差分自回归移动平均模型得到确定性需求的表达式和随机性需求的分布函数,对单列车随机票额分配问题进行了研究。客流预测具有不确定性,在随机需求下研究旅客列车的票额分配方法更符合实际情况。但随机需求条件下票额分配的模型和求解更加复杂,所以单列车的客流预测和票额分配方法是国内外学者的主要研究对象,对多列车票额分配方法的研究较少,特别是不同列车多种停站方案对票额分配的影响考虑不足。我国高速铁路路网规模庞大,运输需求更加复杂,为了满足不同OD客流需求,在编制开行方案阶段就设计了不同列车的多种停站方案。提供相同OD客运服务的旅客列车之间具有可替代性,现有的先客流分配再票额分配的方法缺乏对收益提高的整体考虑,不利于从全部旅客列车角度提高运输收益。
针对以上不足,本文重点考虑了不同列车多种停站方案对票额分配的影响,在各OD随机需求下直接以所有旅客列车收益最大为目标构建多列车多停站方案的票额分配模型,针对模型离散非线性特点设计粒子群算法进行求解。同时对比先客流分配再以单列车收益最大为目标的票额分配方法。
1 模型构建
1.1 停站方案对票额分配的影响
停站方案是在列车运行路径、类别、开行对数确定后,根据客流需求及列车协调配合情况确定各列车的停站序列。列车停站方案主要有三种基本模式:大站停列车、交错停列车、站站停列车。大站停列车是指选择沿途全部或部分客流量较大或有特殊需求的车站停靠的列车;交错停列车除在沿线大站停靠外,同时也选择部分小站停靠,是大站停和站站停模式的有机结合,是高速铁路旅客列车停站方案的主要模式;站站停列车在运行区段中的各个车站均停靠,对未满足客流需求和服务频率要求的车站提供服务,并实现所有站间客流的可达性。
如图1所示,一条高速铁路上共有A、B、C、D 4个停靠站,两列旅客列车,其中列车1在A、B、D停靠,列车2在A、B、C、D停靠。假设各列车定员为560人,客流需求:(A,D)840人,(A,B)280人,(C,D)280人。方案1不考虑列车停站方案的差异,将客流需求平均分配,将有(C,D)140人的客流需求因无可利用席位而不能被满足;方案2根据列车停站方案的不同对票额进行了调整,各OD客流需求均得到了满足。
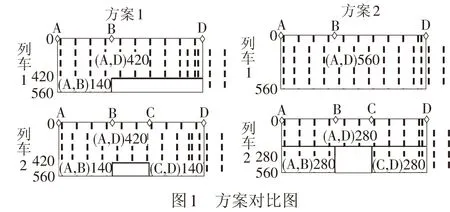
从上述票额分配方案的例子不难看出,列车停站方案影响票额分配方案,实际路网中的停站方案复杂多样,只有在整体对不同列车的多种停站方案进行考虑,才能制定更合理的票额分配方案,提高席位利用率和运输收益。
1.2 数学模型
(1) 问题描述
相邻停靠站(能够办理旅客乘降作业)之间的路段称为区段;一个或多个连续区段构成的旅行线路称为路径(OD),其基本特征为途径区段、线路长度、客流需求、车票价格等。
假设一条由L+1个停靠站和L个区段组成的高速铁路上开行了n列旅客列车并有多种停站方案。不同旅客列车同一OD上具有相同的单一票价,各OD上的客流需求由已知的正态分布函数进行描述。只提供有座车票且不允许超售,以整条高速铁路客票收益最大为目标,以各列车各区段的席位能力为约束,优化所有旅客列车的票额分配方案。
(2) 符号定义
m表示运行区段,m=1,2,…,L,整条高速铁路包括L个运行区段,L+1个停靠站;G表示旅客列车集合,g∈G,g=1,2,…,n;(i,j)表示一个或多个连续区段构成的OD,其中i为OD的起点车站,j为OD的终点车站;Cgm表示列车g在运行区段m上提供的最大席位能力;fij(x)表示(i,j)上的客流需求概率密度函数;μij表示(i,j)上客流需求的平均值;σij表示(i,j)上客流需求的标准方差;pij表示(i,j)上的车票价格;ugij为列车g能否在(i,j)提供服务的0-1判断变量,若列车g在i车站和j车站均有停靠,则ugij=1,否则ugij=0;bgij表示列车g为(i,j)提供服务的票额限制决策变量,当ugij=1时,bgij≥0,当ugij=0时,bgij=0。
(3) 模型建立前提和相关参数计算公式
借鉴文献[1]描述客流需求的方法,各OD客流需求服从独立正态分布,则(i,j)客流需求的概率密度函数为
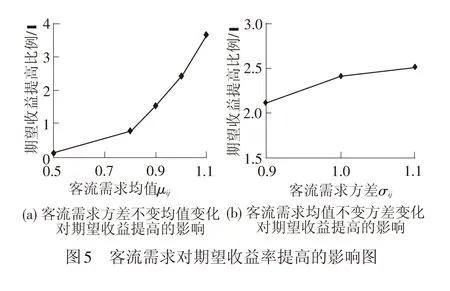
1≤i ( 1 ) 每列旅客列车共有L(L+1)/2个票额限制决策变量,当有n列旅客列车时,共有n×L×(L+1)/2个票额限制决策变量,这里设置一个N=n×L×(L+1)/2的搜索空间,对应向量B=(b111,b112,…,bgij,…),其中元素bgij在B中的位置为 0.5(n-1)L(L+1)+ ( 2 ) 若列车g在(i,j)的客流需求概率密度函数fgij(x)可求,借鉴文献[2]的单列车客票期望销售量计算方法,列车g在(i,j)的客票期望销售量为 ( 3 ) ( 4 ) 式中:Rgij表示列车g在(i,j)的客票期望收益。 n列旅客列车在(i,j)的客票期望收益为 ( 5 ) n列旅客列车的客票期望收益为 ( 6 ) 现有的铁路12306购票系统是将客票和席位对应出售,即列车g在(i,j)的某一席位对应的客票一旦售出,则在(i,j)途径的区段上该席位不能被再次利用,本文只考虑有座车票且不考虑超售,所以bgij满足 ∀g,m ( 7 ) (4) 多列车多停站方案票额分配模型 基于预测的各OD客流需求,以高速铁路客票收益最大为目标,以各列车各区段的最大席位能力为约束,建立高速铁路多列车多停站方案票额分配模型为 ( 8 ) s.t. ∀g,mbgij为整数 ∀g,i,j ( 9 ) (ugij-1)bgij=0ugij=0,1 bgij≥0 ∀g,i,j (10) 本文提出的多列车多停站方案票额分配模型为非线性整数规划,对于这类问题,粒子群算法易于提高初始解、所需设置参数少、占用内存空间小、大规模问题的求解性能优异。粒子群算法是由Kennedy和Eberhart[12]在1995年源于鸟类捕食行为的研究提出的。使用粒子群算法需要解决初始解的生成、粒子适用值的计算方法、粒子位置的更新规则等问题,根据前述票额分配模型,求解算法如下。 (1) 初始解的生成 在非确定性客流需求条件下,本文提出的模型为非线性整数规划,难以实现精确求解,若将客流需求变为确定值,则该问题将转化为线性规划。因此在初始解生成阶段,将非确定性客流需求的平均值作为确定性客流需求取值,松弛整数约束,建立线性规划模型进行求解,并将求得最优解作为粒子群算法初始解的生成向量。确定性客流需求下的线性规划模型为 (11) s.t. ∀g,m (12) (13) (ugij-1)bgij=0ugij=0,1bgij≥0 ∀g,i,m (14) (15) 式中:rh的各分量服从(-r,r)上的均匀分布,r为整数,其大小可根据实际情况而定。 (2) 粒子适用值计算 (16) (3) 粒子位置更新 (17) (18) (19) (20) 算法流程见图2,具体步骤为 Step2设置种群规模Psize和ω,γ1,γ2等相关参数。 Step3计算所有粒子的适用值并记录。 Step4设置输入参数l=0,h=1,Kmax=500。 Step10若h Step11如果l Step12输出所有粒子的最佳位置对应的向量B和其适用值T。 考虑一个由7个区段、8个停靠站组成的高速铁路,列车按8节编组,每列旅客列车在每个区段的最大席位能力均为560个席位。该高速铁路服务28个OD,需求均值和标准差均为常数。某一时段内共有4列旅客列车,其中大站停列车1列,交错停列车2列,站站停列车1列。具体停站方案及站间距离,见图3,参数pij、μij、σij取值见表1。 设定粒子群规模Psize=25,最大迭代次数500次,收敛控制因子ω=0.5,γ1=0.5,γ2=0.5,借助于Matlab工具进行模型求解。表2为确定性客流需求下线性规划模型的计算结果,即初始解生成向量,给出了每列旅客列车各OD票额限制。表3给出了粒子群算法求解的最终票额分配方案,图4为求解过程,算法在迭代到150步时达到收敛。 表1 参数取值(pij,μij,σij) 以相同的客流需求为基础,尽量满足长途客流需求并以人公里数最大为目标进行客流分配,再以单列旅客列车客票收益最大为目标进行票额分配,可以求得票额分配方案。表4为求得的方案,称为对比方案。 在相同的客流需求下,对比方案的客票期望收益为76.368万元,本文方案的客票期望收益为78.211万元,期望收益提高约2.41%。因此本文方案不但简化客流分配过程实现多列车1次性优化,同时说明站在收益角度从整体优化不同停站方案旅客列车间的相互协调对收益提高有着明显影响。 在客流需求方差不变的情况下,客流需求较大时,本文方案期望收益提高较大;客流需求较小时,因席位能力充足,大部分客流需求在两种方案下都能得到较好满足,期望收益差别较小。如图5(a)所示,当客流需求减小为0.5μij时,两种方案的期望收益已无明显差别。 对比方案第一阶段整体优化时未考虑客流波动的影响,在第二阶段单列车票额分配再考虑客流波动,因协调空间变小,客流波动影响较大;本文方案从整体考虑客流波动情况,能够更好地避免客流波动造成的影响。如图5(b)所示,在客流需求均值不变的情况下,客流波动越大,相比之下本文方案越优。 表2 初始解生成向量(列车1,列车2,列车3,列车4) 表3 多列车多停站方案票额分配结果(列车1,列车2,列车3,列车4) 表4 对比方案票额分配结果(列车1,列车2,列车3,列车4) 本文研究了多列车多停站方案的票额分配方法,根据建立的模型特点设计粒子群算法进行求解,并将本文提出方法和先客流分配再票额分配的方法进行了对比。结果表明,多列车多停站方案的票额分配方法能够更好地对不同停站方案的旅客列车进行协调,站在整个线路所有旅客列车的角度提高客运收益。本文所得的控制方法仍是静态的,但在预订过程中不断更新客流需求和席位能力也能达到动态的效果。同时本文仅考虑了单一票价形式,多等级票价及其嵌套方式等收益管理问题是进一步研究的方向。 参考文献: [1] CIANCIMINO A, INZERILLO G, LUCIDIS, et al. A Mathematical Programming Approach for the Solution of the Railway Yield Management Problem[J]. Transportation Science, 1999, 33(2): 168-181. [2] YOU P S. An Efficient Computational Approach for Railway Booking Problems[J]. European Journal of Operational Research, 2008, 185(2): 811-824. [3] ONGPRASERT S. Passenger Behavior on Revenue Management Systems of Inter-city Transportation[D]. Japan: Kochi University of Technology, 2006. [4] BHARILL R, RANGARAJ N. Revenue Management in Railway Operations: A Study of the Rajdhani Express, Indian Railways[J]. Transportation Research Part A, 2008, 42(9): 1 195-1 207. [5] 史峰,陈彦,周文梁,等. 基于用户平衡分析的铁路旅客列车票额分配计划制定及评价方法[J]. 中国铁道科学,2008,29(6):98-103. SHI Feng, CHEN Yan, ZHOU Wenliang, et al. Railway Passenger Train Seats Allotment Plan Establishment and Evaluation Method Based on User Equilibrium Analysis[J]. China Railway Science, 2008,29(6):98-103. [6] 蓝伯雄,张力. 高速铁路客运专线的收益管理模型[J]. 中国管理科学,2009,17(4):53-59. LAN Boxiong, ZHANG Li. Revenue Management Model for High-speed Passenger Railway[J]. Chinese Journal of Management Science,2009,17(4):53-59. [7] 单杏花,周亮瑾,吕晓艳,等. 铁路旅客列车票额智能预分研究[J]. 中国铁道科学,2011,32(6):125-128. SHAN Xinghua, ZHOU Liangjin, LÜ Xiaoyan, et al. Research on Intelligent Pre-assignment of Ticket Allotment for Railway Passenger Train[J]. China Railway Science, 2011,32(6):125-128. [8] 钱丙益,帅斌,陈崇双,等. 基于旅客buy-up行为的铁路客运专线收益管理模型[J]. 铁道学报,2013,35(8):10-15. QIAN Bingyi, SHUAI Bin, CHEN Chongshuang, et al. Revenue Management Model for Dedicated Passenger Line Based on Passengers’ Buy-up Behavior[J]. Journal of the China Railway Society, 2013,35(8):10-15. [9] 包云,刘军,马敏书,等. 高速铁路嵌套式票额分配方法研究[J]. 铁道学报,2014,36(8):1-6. BAO Yun, LIU Jun, MA Minshu, et al. Nested Seat Inventory Control Approach for High-speed Trains[J]. Journal of the China Railway Society, 2014,36(8):1-6. [10] BAO Yun, LIU Jun, MA Minshu, et al. Seat Inventory Control Methods for Chinese Passenger Railways[J]. Journal of Central South University, 2014(4):1 672-1 682. [11] 包云,刘军,刘江川,等. 基于随机需求的单列车票额分配方法[J]. 中国铁道科学,2015,36(2):96-102. BAO Yun, LIU Jun, LIU Jiangchuan, et al. Seat Allotment Method for Single Train Based on Stochastic Demand[J]. China Railway Science, 2015,36(2):96-102. [12] KENNEDY J, EBERHART R. Particle Swarm Optimization[C]//Proceedings of the IEEE International Conference on Neural Networks. Perth, Australia: IEE,1995:1 942-1 948. [13] PARK C, SEO J. Seat Inventory Control for Sequential Multiple Flights with Customer Choice Behavior[J]. Computers and Industrial Engineering, 2011(11):1 189-1 199. [14] LAN Y, BALL M O, KARAESMEN I Z, et al. Analysis of Seat Allocation and Overbooking Decisions with Hybrid Information[J]. European Journal of Operational Research, 2015(1):493-504.


2 求解算法






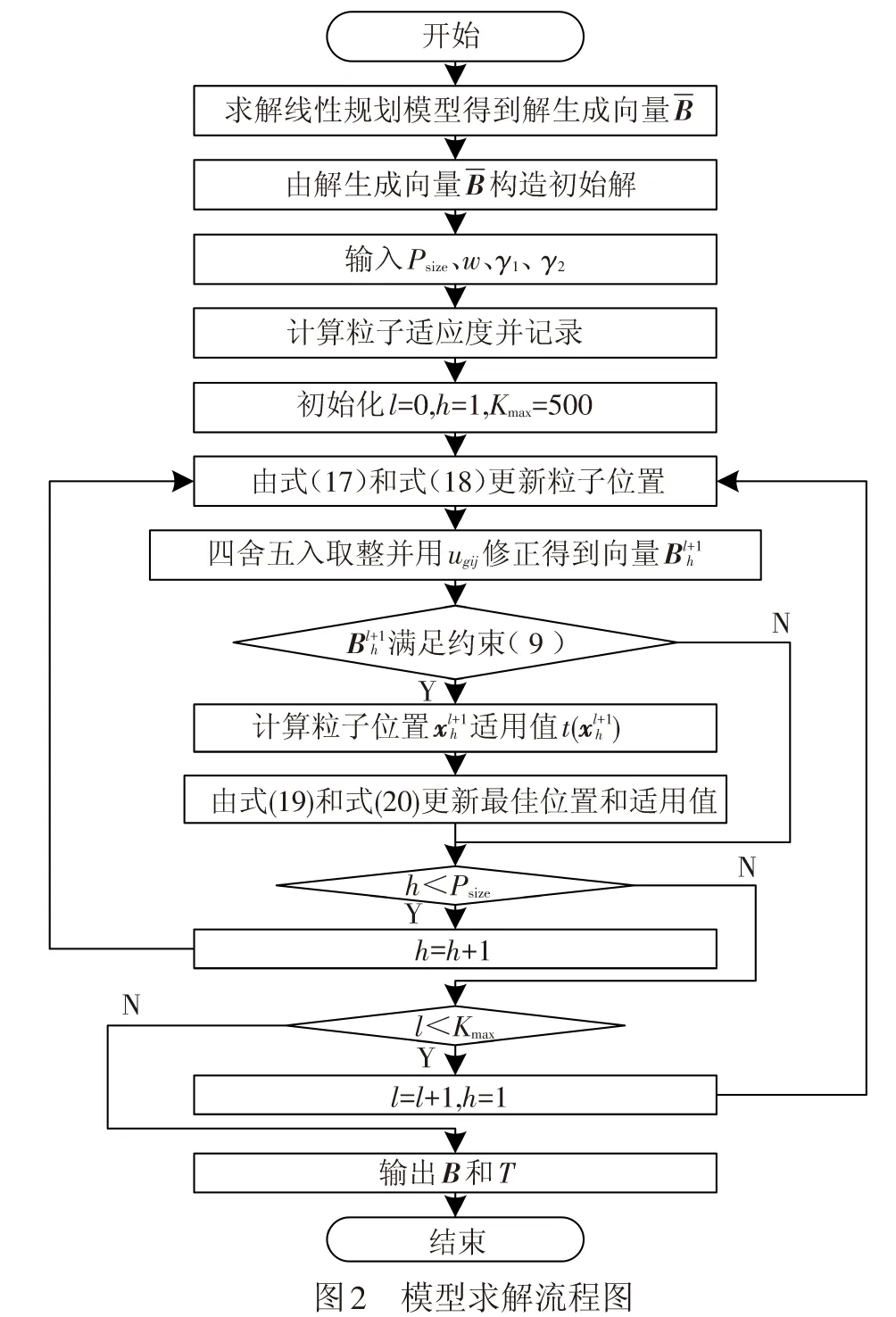

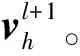

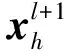

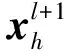
3 算例






4 结论

