基于核仿射传播聚类雷达信号分选
刘志鹏, 田桢熔, 毛 重
(1.空军航空大学 信息对抗系, 吉林 长春 130022;
2.空军航空大学 飞行训练基地, 吉林 长春 130022;
3.空军航空大学 信息管理中心, 吉林 长春 130022)
基于核仿射传播聚类雷达信号分选
刘志鹏1,田桢熔2,毛重3
(1.空军航空大学 信息对抗系, 吉林 长春130022;
2.空军航空大学 飞行训练基地, 吉林 长春130022;
3.空军航空大学 信息管理中心, 吉林 长春130022)
摘要:将一种新的仿射传播聚类算法引入雷达信号分选,对仿射传播聚类算法的相似度计算和评价指标进行改进和简化,提高了分选性能。实验结果证明,本方法在不同的测试环境下均可以取得较好的分选效果。
关键词:信号分选; 聚类算法; 核方法; 评价指标
0引言
由于缺少先验信息,对未知雷达信号的分选需利用参数自身的分布特点和规律进行去交错处理。聚类方法是一种无监督的学习方法[1],在缺少先验信息的情况下,利用数据本身的相似度和一定的评价准则来完成分类,从而发现数据集的内在组织结构,其优良的特性非常适合对未知雷达信号的分选。
近年来,国内外学者讨论较多的聚类方法如k-means聚类[2]、网格密度聚类[3]、C-均值模糊聚类[4]等,存在着诸如对初始条件敏感、对类边缘数据及高维数据处理不佳、需反复迭代等问题,因而并未在雷达信号分选中得到广泛应用。
仿射传播聚类是Frey B J[5]等在Science上提出的一种新型聚类算法,不同程度上克服了上述聚类算法的不足,具有处理速度快,聚类准确性高,可以自适应给出聚类数目等优点,文中即利用仿射传播聚类算法对雷达信号进行分选。但由于复杂体制雷达信号参数的分布和变化特征都极其复杂,而核方法通过将信号参数映射到高维空间中,把复杂的非线性分类问题转化为高维特征空间中的线性分类或近似线性分类问题,文中为了提高仿射传播聚类算法的性能,将核方法引入到分选过程中,提出核仿射传播聚类算法。
1仿射传播聚类算法原理
仿射传播聚类(AP)算法的本质是将各数据点视为网络中的节点,通过各节点间信息的不断交换,选出代表节点,从而完成聚类。算法首先构造相似度矩阵,在此基础上,计算数据点间的吸引度(responsibility)和归属度(availability)用以表示数据点间信息的传递和竞争,经过有限次迭代后,得出最优聚类结果。
1.1相似度矩阵及偏置
在初始状态时,将每个数据点都视为潜在的代表点(聚类中心),并计算相似度矩阵s,原始的AP算法的相似度采用欧式距离平方的负值,即s(i,k)=-‖xi-xk‖2,其中i≠k,即xi,xk为两个不同的数据点。s(k,k)为偏置值,需预先设定,利用s(k,k)值可以控制聚类数目的大小,一般将s(k,k)设为总相似度的平均值,文献[6]证明AP算法对初值不敏感,因此初始参数的选择较为宽泛。
1.2吸引度和归属度的计算
定义r(i,k)和a(i,k):r(i,k)为数据点xi向数据点xk发送的吸引度信息,r(i,k)表示xk作为xi的代表点的合适程度;a(i,k)为xk向xi发送的归属度信息,a(i,k)搜集其他数据点支持xk作为代表点的证据信息,反映xk作为xi代表点的可信度;二者之和作为xk是否为代表点的证据。数据点间信息传递原理如图1所示。

图1数据点信息传递示意
二者的计算方法为:
(1)
(2)
1.3迭代更新及聚类生成
由式(1)计算出所有数据点的吸引度r(i,k)后,即可根据r(i,k)通过式(2)计算每个数据点的归属度a(i,k),再利用a(i,k)的新值依据式(1)计算r(i,k),以此进行循环迭代,从而完成数据点间的信息交换。为了防止迭代过程发生大幅度震荡,采用衰减因子λ控制更新速率,不妨设当前过程为第j个循环阶段(j≥2),更新规则如下:
(3)
(4)
式(3)、式(4)中右侧的rj,aj为当前吸引度和归属度依据式(1)、式(2)的计算值,式(3)、式(4)左侧rj,aj为当前循环确定的吸引度和归属度的最终值,rj-1和aj-1为上一个循环阶段吸引度和归属度的最终值。对于点xi,在循环过程的任一阶段,搜索到r(i,k)+a(i,k)的最大值,可以做出如下判断:
1)若k≠i,则xk为xi的代表点;
2)若 k=i,则xi本身为一个代表点。
在第j个循环找到所有点xi(i=1,2,…,N)的代表点xk(k=1,2,…,m),把代表点看成聚类中心,其所代表的数据点即为该聚类的成员,于是就得出了该阶段的聚类结果。迭代的终止条件为是否满足聚类评价指标或达到最大迭代次数。聚类评价指标一般采用Silhouette指标[7]:假设n个数据点被划分成m个类,其中某个类为Ci(i=1,2,…,m),p为Ci中的一个样本,I(p)为聚类中样本p与Ci中其他样本的平均距离;Ci(i′≠i)为有别于Ci的另一个类,设d(p,Ci′)为样本p到Ci′中所有样本的平均距离,Dp=min{d(p,Ci′)},其中i′=1,2,…,m且i′≠i;于是可得样本p的Silhouette指标为
(5)
由式(5)可计算出聚类Ci中每个样本的Sil值,进而求出所有类的平均值Sav(C),通过观察式(5)不难发现,Sav(C)通过类内数据的平均距离反映类内的离散程度,通过最小类间距离反映不同类的可分性,Silhouette指标正是综合以上两个因素估计聚类质量的优劣,其值越大,代表聚类质量越好。
仿射传播聚类算法已在人脸识别、寻找基因外显子、航线规划等领域得到成功实践,已证实其具备聚类速度快、聚类结果可靠、适合处理大类别、特征分布不规则的数据等优点。然而,该算法的数据间相似度是利用欧式距离的负值来表征的,文献[8]已证明,采用欧氏距离作为相似性测度的聚类方法,在处理非线性分类问题时,分类性能会严重下降。现代体制雷达信号参数变化复杂,具有非线性分布的性质,因此,若直接利用该算法进行雷达信号分选,则无法更好地提高分选的准确率。为此,文中引入核方法来改进相似度计算,并简化聚类指标计算,提出核仿射传播聚类算法(KernelizedAffinityPropagationClustering,KAPC)。
2核方法原理
核方法是机器学习中为处理非线性分类问题而发展起来的一种技巧,顾名思义,核方法通常采用核函数替代数据间的内积运算,将数据特征向量映射到高维的特征空间,从而使得在低维状态下不易发掘的特征在高维度的特征空间得到凸显,进而使复杂的非线性分类问题转化为较为简单的线性分类问题[9]。核方法高效巧妙处理非线性问题的能力使其在模式识别、预测、综合评价等问题中得到广泛应用。核方法将非线性分类问题转化为线性分类的思想如图2所示。

图2核方法思想示意图
但是,我们通常不能确知非线性映射Φ(·)的具体形式,然而通过选择满足Mercer半正定的核函数κ(xi,xj),可以建立高维空间的内积运算即〈Φ(xi),Φ(xj)〉与低维空间原数据点间的关系:
(6)
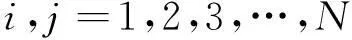
常用的核函数有:
1)多项式核
(7)
式中:d----多项式阶数。
2)高斯核
(8)
式中:β----高斯核宽度。
此外,由于升维映射是通过核函数隐式定义的非线性映射实现的,因此其内积运算就是利用原数据空间样本间的运算进行的,计算量并未因为维数的增多而增多。文中在仿射传播聚类的基础上,引入核方法来构建雷达信号分选模型,即是考虑到了其处理特征分布复杂、分类边界非线性的数据所具有的优势。
3基于KAPC算法的雷达信号分选
3.1核方法下的相似度
引入非线性映射Φ:x→Φ(x)∈H,从而原数据空间的数据点被映射到高维核空间H中,则平方欧式距离可表述为:
(9)
式中i≠j,采用式(9)来代替原算法定义的欧式距离平方负值,作为新的相似性测度。同时,构造核矩阵Κ
(10)
矩阵中每个元素为两个样本在高维空间内积的结果,其大小表征了样本间的相似性,其值越大,样本属于同类的概率就越大;反之,元素的值越小,对应样本的相似度越低,于是,利用核矩阵Κ代替原算法的相似矩阵S。此时,预设偏置为Κ(i,i),吸引度的计算方法变形为下式
(11)
而归属度的计算基于式(2)且形式不变。
3.2核方法下简化的聚类指标

(12)

首先定义中心判别矩阵和聚类指标矩阵。
1)中心判别矩阵。
将每个样本点的吸引度和归属度之和作为元素构成中心判别矩阵Z,则有

(13)
注意,此时r(i,k)与a(i,k)已进行核化处理,搜索矩阵Z中每一行的最大值元素,设Z=(z1,z2,…,zn)T,Z(i,k')=max(zi),则数据点k′是数据点i所在类的聚类中心。
2)聚类指标矩阵。
将中心判别矩阵Z中的行最大值元素置1,其余元素置0,并由此构成中心指标矩阵W,设W=(w1,w2,…,wn),其中wj(j=1,2,…,n)为构成W的列向量,则元素不全为0的列向量wj′即为所形成的子类,wj′中非零元素的行坐标对应类j′所包含的样本点,sum(wj′)为类j′成员的个数。
3)反聚类指标矩阵。
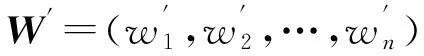
于是,若假设样本点p属于类j′,则p与同类样本点的平均相似度Ip可由下式获得
(14)
式中:kp----矩阵K中第p行构成的行向量;
wj′----类j′所对应的指标矩阵的列向量。
样本点p与其他类样本平均相异度为
(15)
进而得出
(16)

(17)

3.3 基于核仿射传播聚类算法的雷达信号分选流程
由于实际信号环境中存在着干扰脉冲,这些干扰脉冲有可能形成小样本数的类,从而造成误分选,因此,设定阈值Thsmall,当某类别的脉冲个数小于Thsmall时,将其判定为小样本数的类,这些小样本数的类可能属于某部雷达,也可能是干扰噪声,因此需对这些小样本数的脉冲组进行后续判断。
综上,通过核方法改进相似度计算及简化聚类评价指标后,基于KAPC算法的雷达信号分选流程总结如下:
1)对分选特征进行归一化处理;
2)初始化聚类参数,包括偏置值K(i,i)、衰减因子λ以及最大迭代次数;
3)设定核参数并计算核相似度矩阵K;
4)计算样本间的吸引度和归属度,并进行迭代更新;
5)生成聚类中心和各子类成员,并判断是否收敛,若收敛,或达到最大迭代次数,则转到步骤6),否则返回步骤4);
6)根据聚类指标矩阵和反聚类指标矩阵计算每个聚类结果对应的修改Silhouette指标,判断最优的聚类结果,并识别出小样本数的类别,流程如图3所示。
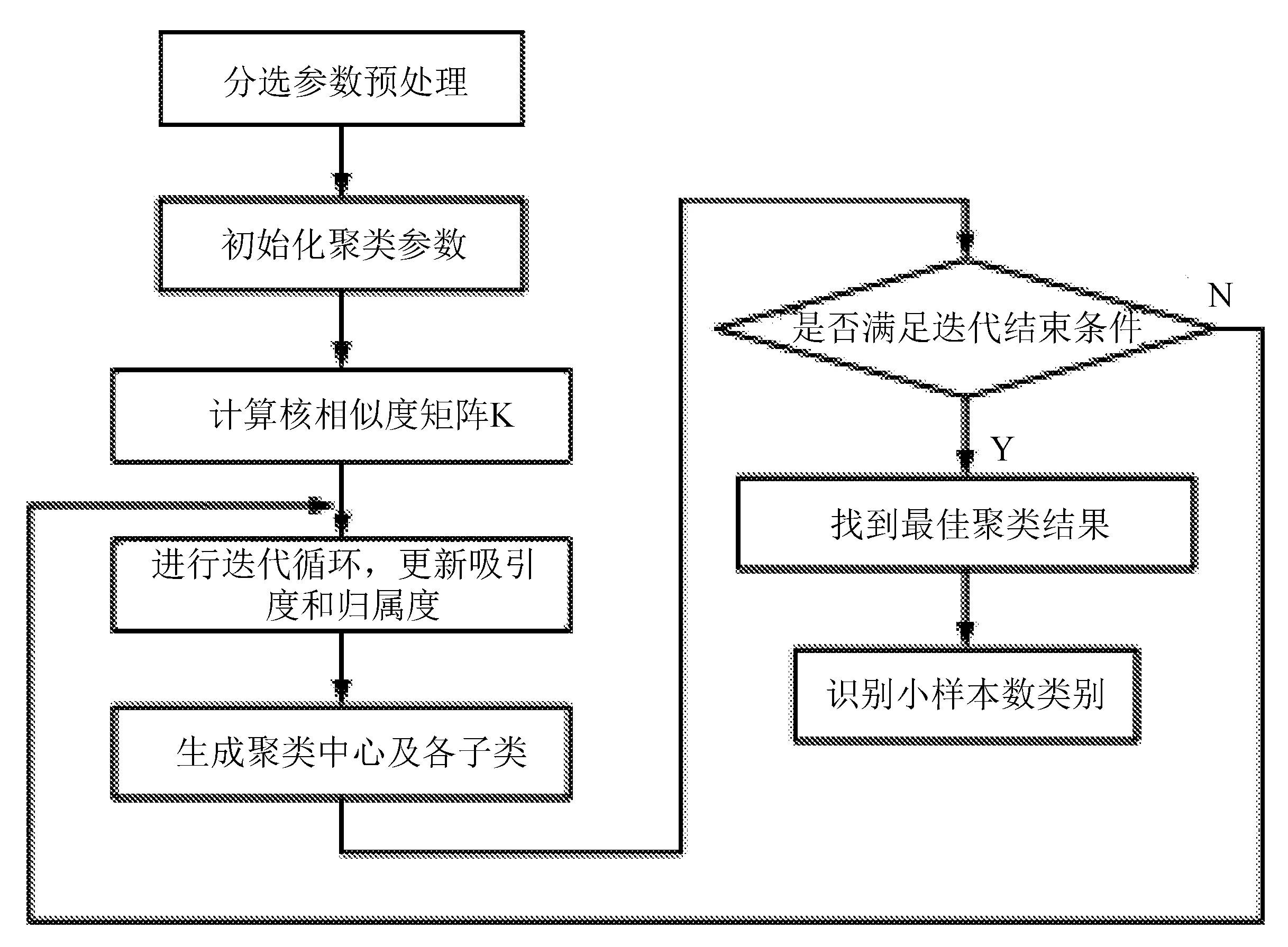
图3KAPC流程示意图
4 仿真实验
仿真环境:Windows 7,AMD CPU A6,4 GB 内存,编程工具为MATLAB 7.10.1。分别利用生成的仿真信号和实际的侦察数据对算法进行验证。
4.1 仿真信号
实验数据为模拟的典型雷达全脉冲数据,按脉冲到达时间顺序生成方向相近的交叠脉冲串,考虑到实际侦察中存在的脉冲丢失及干扰脉冲会影响分选结果,因此向脉冲串引入一定量的丢失和干扰脉冲,脉冲参数及脉內调制特征见表1。
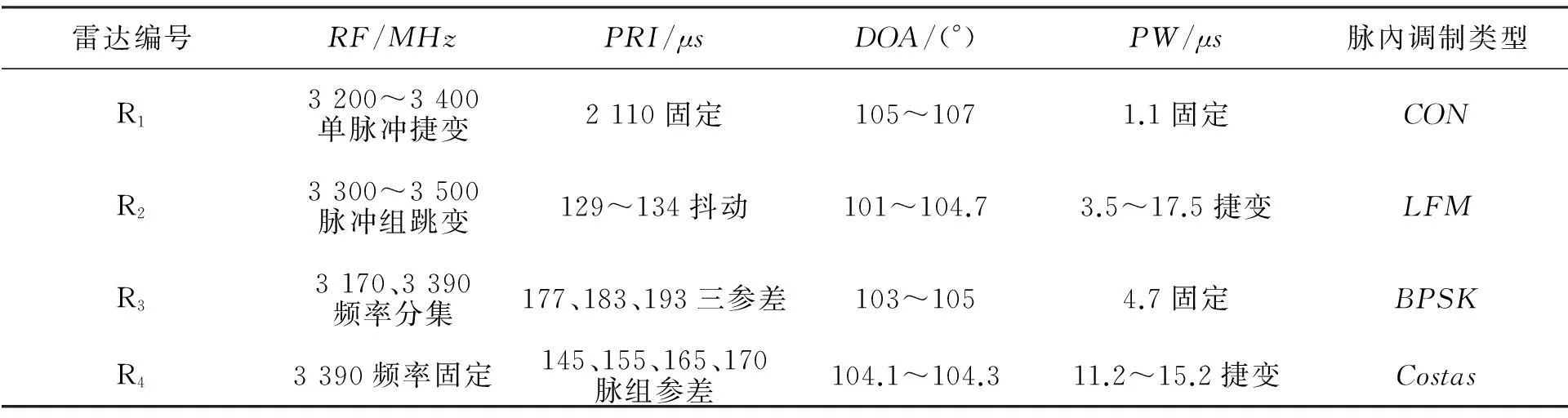
表1 仿真数据典型脉冲参数
初始化KAPC算法参数,选择高斯核作为核函数,文献[10]通过大量雷达数据试验验证高斯核的分类能力,证实当核宽度β≥0.5时,分类准确率最高,文中取β=0.707;偏置值阵K(i,i)设为核矩阵阵K元素的平均值、衰减因子λ=0.5,最大迭代次数设为40次。
当脉冲个数达到2 000时,分别测试KAPC算法在脉冲丢失及加入干扰脉冲情况下的分选正确率,并与原始AP算法,模糊C-均值算法及修正PRI算法进行对比。分选正确率定义为:
模糊C-均值算法及修正PRI算法的参数设置分别同文献[1]和文献[11],脉冲丢失率和干扰脉冲量从0变化到40%时,不同算法的分选正确率曲线对比如图4所示。

(a) 脉冲丢失下的正确率

(b) 加干扰脉冲的正确率
从图4可以看出,在没有脉冲丢失和脉冲干扰的理想情况下,KAPC算法的分选正确率几乎为100%,高于其他几种常见的分选算法;随着脉冲丢失和干扰脉冲的增多,分选正确率有所下降,但仍能接近90%,高于其他算法,且可以看出,虽然修正PRI变换算法的性能在理想情况下接近KAPC算法,但是一旦分选数据质量下降,分选的准确性迅速下降。
为验证KAPC算法的处理速度,采用表1数据进行测试,并与原始AP算法、修正PRI算法及模糊C-均值算法进行比较。参数设置同上,不断增加每部雷达的脉冲数,1 000次蒙特卡洛实验后,得到脉冲数与处理时间的关系如图5所示。

图5 处理速度对比
从图5可知,AP算法处理速度明显优于其他算法,而改进后的KAPC算法在实时性上与原始AP算法相比又有了进一步的提高。
4.2实际信号
为验证KAPC在实际分选中的性能,选择实际侦察数据作为实验数据,利用不同方法得出分选结果,并将分选结果与人工分析后的结果比对,得到的分选正确率记录见表2(KAPC算法及其它各算法的参数设置同上节)。
从表2可以看出,KAPC在实际数据测试中仍能保持90%以上的分选正确率,其它的分选方法均低于90%,证实了KAPC算法良好的分选性能。

表2 实际数据测试结果 %
5 结语
研究了对未知雷达信号的分选方法,针对目前几种聚类方法存在的不足,提出了核仿射传播聚类算法,即利用核内积运算代替原仿射传播聚类的相似度计算,在此基础上利用指标矩阵简化了聚类评价指标的计算,并对小样本数据进行噪声识别。仿真实验表明,该算法性能优于其他算法,在不同信噪比的环境下均具有良好的分选性能,且运算速度快,适合处理大规模脉冲数据集。
参考文献:
[1]尹亮,潘继飞,姜秋喜.基于模糊聚类的雷达信号分选[J].火力与指挥控制,2014,39(2):52-57.
[2]张忠平,王爱杰,陈丽萍.一种基于广度优先搜索的K-Means初始化算法[J].计算机工程与应用,2008,44(27):159-161.
[3]向娴,汤建龙.一种基于网格密度聚类的雷达信号分选[J].火控雷达技术,2010,39(4):67-72.
[4]杨多.复杂环境下多参数雷达信号分选算法研究[D].哈尔滨:哈尔滨工程大学,2012:56-60.
[5]FreyBJ,DueckD.Clusteringbypassingmessagesbetweendatapoints[J].Science,2007,316(5814):972-976.
[6]MichaelJ.Brusc,Hans-FriedrichKohn.Commenton“Clusteringbypassingmessagesbetweendatapoint”[J].Science,2008,319:726.
[7]JoshuaZH,MichaelKN,RongHongqiang,etal.Automatedvariableweightingink-meanstypeclustering[J].IEEETransactiononPatternAnalysisandMachineIntelligence,2005,27(5):657-668.
[8]王开军,张军英,李丹,等.自适应仿射传播聚类[J].自动化学报,2007,33(12):1242-1246.
[9]纪秋颖,林健.基于核方法的聚类算法及其应用[J].北京航空航天大学学报,2006,32(6):747-750.
[10]普运伟.复杂体制雷达辐射源信号分选模型与算法研究[D].成都:西南交通大学,2007:69-70.
[11]罗长胜,吴华,程嗣怡.一种对重频调制与抖动信号的PRI变换分选新方法[J].电讯技术,2012,52(9):1491-1496.
A radar signal de-interleaving method based on kernelized affinity propagation clustering
LIU Zhipeng,TIAN Zhenrong,MAO Zhong*
(1.Information Countermeasure Department, Aviation University of Air Force, Changchun 130022, China;2.Flight Training Base, Aviation University of Air Force, Changchun 130022, China;3.Information Management Center, Aviation University of Air Force, Changchun 130022, China)
Abstract:A new affinity propagation clustering algorithm is applied to radar signal sorting for improving and simplifying the similarity calculation and evaluation indexes, so the sorting performance is optimized. Experiments verify that the good sorting features can be get with the method.
Key words:signal de-interleaving; clustering method; kernel trick; cluster validity index.
中图分类号:TN 971
文献标志码:A
文章编号:1674-1374(2016)01-0056-07
DOI:10.15923/j.cnki.cn22-1382/t.2016.1.12
作者简介:刘志鹏(1990-),男,汉族,吉林长春人,空军航空大学硕士研究生,主要从事雷达信号分选与主识别方向研究,E-mail:tianrunlan@126.com.
收稿日期:2015-11-16

