谈谈数学解题中的构造法

杨昌海

中图分类号：G632 文献标识码：B 文章编号：1002-7661（2016）08-028-01

在科学技术日新月异的今天，社会所需要的人才是创造性人才，而不在是模仿型人才，因此在现代化的教学过程中应加强学生的创新思维、创造能力的培养。而在数学教学过程中运用构造法解题不仅可以帮助开拓学生求异思维能力，打破常规，创新情境，另辟蹊径，而且巧妙新颖，简捷独到，神形兼备。因此运用构造法解题是一项重要的创造性思维活动。那么运用构造法解题为什么能够开发学生的创造性思维呢？如何才能用好构造法解题呢？这就是本论文所要解决的问题。

例1、设⊿ABC的内切圆与外接圆半径分别为r与R，它的最长的高为h，那么关系式r+R≤h 是否恒成立？

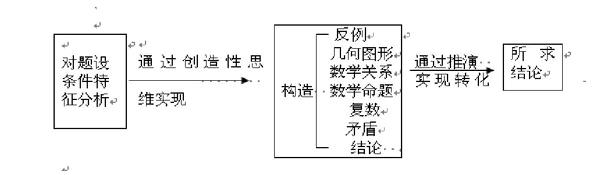
有图形可知，出现r+R>h的情况是钝角三角形。为了构造反例的方便，不妨考虑钝角等腰三角形。设腰长为a，底角为 ，则h=asin

故对于顶角为120°的等腰三角形有r+R≤h。

构造法的解题步骤及解法

通过上面的例子我们对构造法有了一些基本的了解，用构造法解题的关键是对题设条件进行逻辑组合，一般化，特殊化，巧妙地对概念进行分析与综合，构造出一种思维的创造物或想象物，构造法解题过程的模式可用下列框图表示：

过例子从这几个方面阐述构造法的特点极其用法。

一、构造反例

所谓构造反例就是为了说明一个命题不真，常常选择一个符合题设条件但命题不成立的反例。这个过程叫构造反例。选择特殊值，极端情形，常常是构造反例的关键。我们通过下面的例子来看看是如何来构造反例的。

例2、命题“若x，y为无理数，则x 也为无理数”是否成立？

解：不成立。构造反例如下：取无理数 。

若 为有理数，则取x=y= 为反例。

若 为无理数，则取x= ，y= 有x =（ ） = =2，仍为反例。

评注：这里用了二难推理，到底 是有理数还是无理数，并未正面回答，但无论那种情况都提供反例。

二、构造几何图形

在解题时若以数形结合的思想作指导，对于某些复杂的命题，通过构造图形启发思维，借助于图形的直观来解题往往使解题方法简捷。几何证题中的辅助线，代数方程中的是示意图都属于这一类。

例3、求证：

分析：视k*k 为k个边长为k的正方形面积之和，构造如下的几何模型：

上图中所有正方形的面积之和

，⊿ABC的面积

显然 ，所以等式成立。

三、构造数学关系

例4、设a，b都是实数，求证： .

分析：求证结论是二元二次对等不等式，可以以a（或b）为主元构造二次函数，在利用二次函数的性质解决问题。

证明：设 .

因二次项系数大于零，且

= 故 ，

即 .

本题构造一个二次函数在利用根的判别式很好的解决了问题.