一类时滞能源价格模型解的振动性
薛婷婷, 樊小琳, 李 坚, 常治国
(1. 新疆工程学院 基础部, 新疆 乌鲁木齐 830091; 2. 新疆工程学院 采矿工程系, 新疆 乌鲁木齐 830091)
一类时滞能源价格模型解的振动性
薛婷婷1,樊小琳1,李坚1,常治国2
(1. 新疆工程学院 基础部, 新疆 乌鲁木齐 830091;2. 新疆工程学院 采矿工程系, 新疆 乌鲁木齐 830091)
摘要:运用2种方法研究一类时滞能源价格方程在平衡点处的振动性,运用反证法,利用时滞微分不等式与解的关系等方法,建立能源价格方程解的振动准则,通过判定特征方程有无实根,得出方程解振动的2个充分条件.
关键词:时滞能源价格方程; 振动性; 反证法; 特征方程
在微分方程的定性理论研究中,振动性理论作为其中一个重要的研究方向,具有广泛的应用背景[1-4].近年来,国内外众多学者应用时滞微分方程动力学理论[5-7],对能源价格模型做出了大量的研究,并取得了不少的成果[8-10].本文将在前人研究的基础上,进一步研究一类二阶时滞能源价格微分方程[11-12]
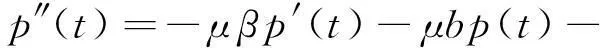
(1)
解的振动性问题,其中β是常数,μ、a、b、τ、d0、g0都是正常数.
1预备知识
定义 1.1方程(1)的非零解p(t)是振动的,如果存在序列{tk},满足tk→∞(k→∞),使得
否则称p(t)是非振动的.
定义 1.2若方程(1)的所有非零解都是振动的,则称方程(1)是振动的.
定义 1.3设x(t,σ,φ)是方程x′(t)=f(t,xt)过(σ,φ)的一个解.若存在τ(σ,φ)≥σ,使得当t≥τ(σ,φ)时,x(t,σ,φ)>0(或x(t,σ,φ)<0),则称x(t,σ,φ)为一最终正解(或最终负解).
注 1从这个定义可知,我们所说的振动解即不是最终正解,也不是最终负解.
2主要结果及证明
(2)

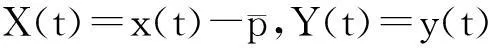
(3)
系统(3)等价于二阶时滞微分方程

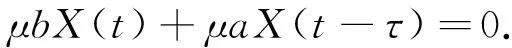
(4)
于是将证明方程(1)所有解振动转化为证明方程(4)所有解振动.下面,介绍2种方法来证明方程(4)所有解振动.
方法1.先消去方程(4)中的一阶导项,再用反证法[13],其中消去方程(4)中的一阶导项,有2种方法.

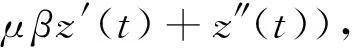
代入(4)式后,化简可得
(5)
即把证明方程(4)的所有解振动,转化为证明方程(5)的所有解振动.
2) 利用积分因子法把(4)式化成类似(5)式的形式.令
(6)
可见κ是t的一次连续可微函数.用(6)式乘(4)式的两端,即可得
(7)
(8)
则有
于是,(7)式简化为
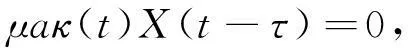
即
其中,κ2(t)可借(8)式化为ξ的函数,即(4)式变换后的方程中一阶导项的系数为0.
证明因为方程(5)是方程(1)线性代换后的方程,两者振动性态一致,所以把证明方程(1)的所有有界解振动的问题转化为证方程(5)的所有有界解振动的问题.若结论不真,则方程(5)存在一个有界解z(t),使得对充分大的t0,有z(t)>0,t≥t0.令t1=t0+τ,则当t≥t1时,有z(t-τ)>0.

因此z′(t)单调递减.下面证明z′(t)>0.
若t2≥t1,使z′(t2)<0,则当t>t2时,存在ηt∈(t2,t),使得
因为上面已证出z′(t)单调递减,所以z′(ηt)≤z′(t2)<0,故
这与z(t)>0矛盾,故当t≥t1时,z(t)>0,z′(t)>0,z″(t)<0.
根据z(t)是一个有界解,令
(9)
则当t充分大时,ω(t)为正,对(9)式两边求导可得
显然ω′(t)<0,因此ω(t)单调递减.从而
即
(10)

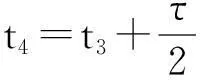
故由不等式(10)可知
将上式分离变量并从g(t)到t积分有
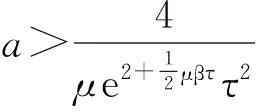
(11)
又因为ex≥ex,对任意的x≥0成立,从而
重复上述做法,则存在序列{tk},满足
(12)
再将(10)式从g(t)到t*积分,于是
这意味着
(13)
类似地有
因此
(14)
合并(13)和(14)式,可以得到
(15)
由(12)和(15)式有
(16)
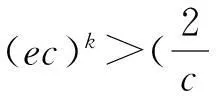
方法2.方程(4)所有解是振动的充要条件是它的特征方程无实根[14].令方程(4)的解eλt,代入可以得到(4)式的特征方程为
(17)
定理 2.2时滞微分方程(1)的所有解具有振动性的充要条件是满足下列条件之一:

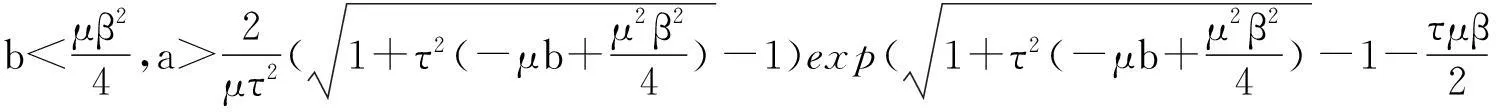
为证明该定理,先给出几个引理[15].
引理 2.1 微分方程(4)所有解是振动的充要条件是它的特征方程(17)无实根.
(18)
其中
(19)
(20)
则有
(21)
(22)
令F′(λ)=0,则记
(23)
下面讨论函数(23)式的性质.
为方便观察,作图1.

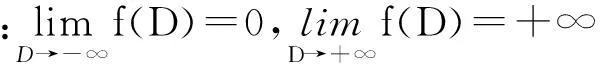
(24)
为函数F(λ)唯一的驻点,即λ0为函数F(λ)唯一的极小点,将(24)式代入方程(17)的右端函数,可得
将μa用(21)式代入,可得
由此及引理2.2,即可得特征方程(17)无实根的充要条件是
(25)
配方为
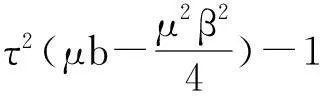
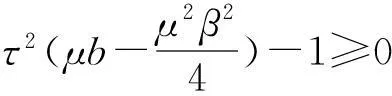
(26)

(27)
时,(25)式可化为
等价为
(28)
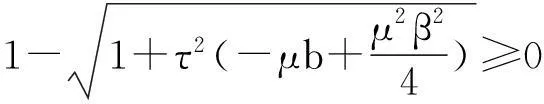

(29)
综合(27)和(29)式知,当
(30)

(31)
在条件(31)式下,(28)式等价于
即
由上文可知,lm+E>0,单调递增,再由(20)式知,上式等价于
简化为
(32)
合并(31)与(32)式,当
时,(25)式成立.
综合上述两方面,即得特征方程(17)无实根的充要条件是满足下列条件之一:
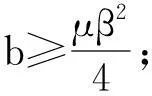

再根据引理2.1,即得微分方程(4)所有解振动的充要条件是满足上述条件之一,又因为微分方程(4)是方程(1)线性代换而来,不影响其振动.所以满足上述条件之一,就可证出方程(1)所有解振动,定理2.2得证,故能源价格方程(1)是围绕平衡点作振动的,即价格是围绕均衡价格作振荡运动的,在正常的经济环境和市场自身的调节下,能源价格会随着时间的推移,围绕均衡价格作振荡运动,价格暂时性的上升或下降属于正常现象,最终将趋向于均衡价格.
致谢新疆工程学院校内科研基金(2013XGY231512)对本文给予了资助,谨致谢意.
参考文献
[1] ROGOVCHENKO Y V, TUNCAY F. Oscillation criteria for second-order nonlinear differential equations with damping[J]. Nonlinear Analysis:TMA,2008,69(1):208-221.
[2] 段永瑞,冯伟,燕居让. 二阶线性时滞微分方程的广义振动性[J]. 系统科学与数学,2001,21(1):72-78.
[3] 黄泽娟,李树勇,周小平. 一类非线性时滞双曲型偏微分方程关于平衡态的振动性分析[J]. 四川师范大学学报(自然科学版),2014,37(6):783-787.
[4] 顿调霞,李永祥. 一类三阶常微分方程的两点边值问题的正解[J]. 四川师范大学学报(自然科学版),2014,37(6):810-813.
[5] SFICAS Y G, STAIKOS V A. Oscillations of differential equations with deviating arguments[J]. Funkcial Ekvac,1976,19:35-43.
[6] 张露,刘瑞宽. 一阶时滞微分方程正周期解的存在性[J]. 四川师范大学学报(自然科学版),2014,37(5):649-652.
[7] 燕居让. 一类二阶非线性脉冲时滞微分方程的振动性[J]. 山西大学学报(自然科学版),2006,29(4):337-340.
[8] 田立新,钱和平. 能源价格的时滞微分方程模型及动力学分析[J]. 江苏大学学报(自然科学版),2010,31(2):240-244.
[9] 邓祥周,田立新,段希波. 能源价格的动态模型及分析[J]. 统计与决策,2007,2:9-10.
[10] 李林. 经济系统中几个微分方程模型[J]. 中国科学院研究生院学报,2003,20(3):273-278.
[11] 薛婷婷,刘文斌,常治国,等. 一类状态依赖时滞能源价格模型的动力学分析[J]. 数学的实践与认识,2012,24(9):162-171.
[12] 薛婷婷,樊小琳,李坚,等. 一类时滞能源价格模型解的稳定性[J]. 数学的实践与认识,2015,14:248-255.
[13] 傅希林,范进军. 非线性微分方程[M]. 北京:科学出版社,2011:249-263.
[14] 郑祖庥,任洪善. 带一阶导数项多滞量二阶中立型方程解的振动的充要条件[J]. 大学数学,1994,S1:156-175.
[15] 刘思明. 两类非线性时滞微分方程的振动性研究[D]. 阜新:辽宁工程技术大学,2012.
2010 MSC:34C10
(编辑郑月蓉)
Oscillation of Solutions for Time-Delay Energy Price Model
XUE Tingting1, FAN Xiaolin1,LI Jian1,CHANG Zhiguo2
(1.DepartmentofBasisTeaching,XinjiangInstituteofEngineering,Urumqi830091,Xinjiang;2.DepartmentofMining,XinjiangInstituteofEngineering,Urumqi830091,Xinjiang)
Abstract:The oscillation of time-delay energy price equation at equilibrium point is researched by two methods. One is proofed by contradiction which uses the measures of time-delay differential relationship between inequality and solutions, and establishes the equations guidelines of energy prices. The other one is to determine whether there exist real roots of the characteristic equation to derive equations with two sufficient conditions.
Key words:time-delay differential equations; oscillation; contradiction; characteristic equation
doi:10.3969/j.issn.1001-8395.2016.01.011
中图分类号:O175.24
文献标志码:A
文章编号:1001-8395(2016)01-0065-06
作者简介:薛婷婷(1987—),女,讲师,主要从事微分方程动力学理论的研究,E-mail:15276831953@163.com
基金项目:新疆自治区高校科研计划基金(XJUEDU2013S44)
收稿日期:2014-10-02

